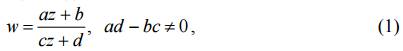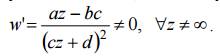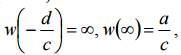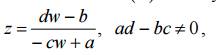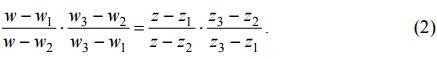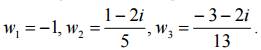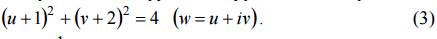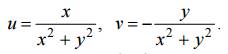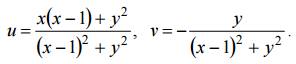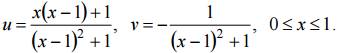- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Глава 3. Конформные отображения
- Геометрический смысл аргумента и модуля производной функции комплексного переменного
- Радикал
- Логарифмическая функция
- Тригонометрические функции
- Теорема Римана. Основные принципы конформных отображений
- Конформные отображения. Примеры
- Конформные отображения. Дробно-линейная функция
- Конформные отображения. Дробно-линейная функция
- 🌟 Видео
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:Конформные отображенияСкачать

Глава 3. Конформные отображения
Видео:Конформные отображения с помощью линейной функцииСкачать

Геометрический смысл аргумента и модуля производной функции комплексного переменного
Пусть дана аналитическая в области $D$ функция $f(z)$. Возьмем точку $z_0in D$, пусть производная функции в этой точке не равна нулю $$f'(z_0)ne0.$$
Функция $w=f(z)$ отображает область $D$ на плоскости z на множество $E$ в плоскости $w$.
Точке $z_0in D$ соответствует точка $w_0=f(z_0)in E$.
Аргумент $arg f'(z_0)$ есть угол поворота касательной к любой кривой, проведенной через точку $z_0$ при ее отображении с помощью функции $w=f(z)$ на плоскость $w$.
Модуль $|f'(z_0)|$ можно рассматривать как величину масштаба в точке $z_0$ при отображении $w$. Если $|f'(z_0 )|>1$, то происходит растяжение бесконечно малого элемента, выходящего из точки $z_0$. Если $|f'(z_0 )| 0rightarrow |w| 0) rightarrow w_0=0. $$
Функция $w=z^n$ отображает расширенную комплексную плоскость $z$ на расширенную комплексную плоскость $w$.
Не является конформным при $z=0$, так как $$w’=n,z^ =0 ,, mbox z=0.$$
Не является однолистной, так как всякая точка $w$, отличная от $w=0$ и $w=infty$, имеет $n$ различных прообразов. Для однолистности отображения следует брать на плоскости $z$ лишь сектор вида $$kcdotdisplaystylefracleqslant mbox,zleqslant(k+1)cdotdisplaystylefrac,,, kin mathbb Z_.$$
Исследуем поведение функции около точки $z=0$. При помощи степенной функции $$ w=z^n $$ угол с вершиной в начале координат плоскости $z$ отображается в угол с вершиной в начале координат плоскости $w$ c раствором в $n$ раз большим: $$ z=rho e^,, rightarrow ,, w = z^n=rho^n e^. $$ Отображение будет взаимно однозначным, если раствор угла на плоскости $w$ будет не более $2pi$.
Найти в какую область преобразуется квадрат $$ 0le xle 1,quad 0le yle 1 $$ функцией $w=z^2+z-1$.
Решение. Выделим вещественную и мнимую части: $$ begin u=x^2-y^2+x-1, v=2xy+y. end $$
Определим образы участков границ данного квадрата: begin OA:quadleft<begin y=0, 0le xle1 endright.quadhboxquad left<begin u=x^2+x-1, v=0. endright. end это отрезок вещественной оси $-1le ule 1$. begin AB:quadleft<begin x=1, 0le yle1 endright.quadhboxquad left<begin u=1-dfrac9, 0le vle3 endright.hskip17.5pt end это часть параболы в первом квадранте.
Образы отрезков $BC$ и $CO$ также являются дугами парабол: beginlabel BC:quad u=frac14big(v^2-9big),quad 1le vle 3, end beginlabel CO:quad u=-1-v^2,quad 0le vle1. end Так как точка $z=displaystylefrac12(1+i)$ переходит в точку $w=i-displaystylefrac12$, то внутренность квадрата переходит во внутренность криволинейного четырехугольника.
Ответ: Внутренность квадрата переходит во внутренность криволинейного четырехугольника.
Видео:Комплексная область Im(1/z)=1/2. ОкружностьСкачать

Радикал
Рассмотрим функцию begin w=sqrt[n], end обратную степенной функции $z=w^n$.
Примем, что $$w=infty mbox z=infty.$$
Во всех точках расширенной плоскости $z$, кроме точек $z=0$ и $z=infty$ (где эта функция соответственно равна $w=0$ и $w=infty)$, эта функция $n$-значна и все ее $n$ различных значений для каждого фиксированного $z=re^$ (не равные 0 и $infty$) дает формула: $$ w=sqrt[n]cdot e^ <itfrac> =sqrt[n]cdot e^ <itfrac>cdot e^<itfrac>quadhbox quad k=0,1,dots,n-1. $$
Через $w_k$ обозначим множество всех точек $w$, соответствующих данному фиксированному значению $k$. В результате получим $n$ функций $w_k$, $k=0,2,dots,n-1$, называемых textcolor $w=sqrt[n]$. $$ w_k= sqrt[n]cdot e^ <itfrac>cdot e^<itfrac>quadhbox quad k=0,1,dots,n-1. $$
Рассмотрим какую-нибудь ветвь $w_k$ функции и заставим точку $z$ описать в плоскости какую-нибудь замкнутую кривую.
Если эта кривая не содержит внутри себя точку $z=0$ (сплошная кривая на рисунке), то непрерывно изменяющийся аргумент точки $z$ вернется к прежнему значению с возвращением точки $z$ в исходное положение. В силу этого и ветвь $w_k$ радикала останется прежней (т.е. мы вернемся к прежнему значению корня в исходной точке).
Картина изменится, если кривая $l$ будет содержать внутри себя точку $z=0$ (пунктирная кривая на рисунке). В этом случае после полного обхода кривой $l$ аргумент точки $z$ в исходном положении увеличится на $pm 2pi k$ (в зависимости от того, совершается ли обход кривой против или по часовой стрелки), в силу чего мы от значения $w_k$ корня в исходной точке перейдем либо к значению $$ w_kcdot e^<itfrac>=w_,$$ либо к значению $$ w_kcdot e^<-itfrac>=w_. $$
Повторяя обход вокруг начала координат в том или ином направлении достаточное количество раз, мы можем перейти от исходной ветви $w_k$ радикала к любой другой ветви. Очевидно, что после $n$ обходов начала координат в одном направлении мы возвращаемся к исходной ветви радикала.
Точка, обладающая тем свойством, что обход вокруг нее переводит от одной ветви многозначной функции к другой ветви, называется точкой разветвления этой функции. Таким образом, точка $z=0$ будет точкой разветвления функции $w=sqrt[n]$.
Из сказанного следует, что мы можем выделить $n$ однозначных ветвей $w_k$ функции $w=sqrt[n]$ только в такой области $D$, которая не содержит ни одной замкнутой кривой, заключающей внутри себя точку $z=0$.
Расширенная плоскость $z$ с любым разрезом от точки $z=0$ до точки $z=infty$ и, в частности, с разрезом вдоль положительной части вещественной оси (левая часть рисунка) не содержит ни одной замкнутой кривой, обходящей точку $z=0$. На ней можно выделить $n$ однозначных ветвей $w_k$, $k=0,1,dots,n-1$, радикала, принимающих каждая одно из значений $sqrt[n]$.
Эти ветви будут однолистно отображать расширенную плоскость $z$ с разрезом вдоль положительной части вещественной оси на секторы $$ kfracn 0$.
Видео:Изобразить область на комплексной плоскостиСкачать

Логарифмическая функция
Логарифмическая функция обратна показательной, бесконечнозначна, все ее значения вычисляются по формуле $$ w=mboxz=mbox|z|+imboxz=mbox|z|+i(mboxz+2pi k),quad k=0,pm1,pm2,dots . $$ Дополнительно примем, что $w=infty$ при $z=0$ и $z=infty$.
Обозначив через $w_k$ множество всех точек $w$, соответствующих данному фиксированному значению $k$, получим бесконечное множество функций, которые называются ветвями многозначной функции $w=mboxz$ $$ w_k= mbox|z|+imboxz=mbox|z|+i(mboxz+2pi k),quad k=0,pm1,pm2,dots . $$
Бесконечнозначность логарифма связана с бесконечнозначностью его мнимой части $mboxz$. Поэтому область не должна допускать обхода начала координат по непрерывной кривой, так как при таком обходе значение $mboxz$ изменяется на $2pi$. Область указанного типа будет сектором концентрического кольца: $$ 0 0, 0 1$.
Для того чтобы лучше представить себе рассматриваемое отображение, положим $$ z=re^,quad w=u+iv $$ и произведя соответствующие замены в функции Жуковског и отделив вещественные и мнимые части, получим два вещественных равенства, зависящие от двух параметров $$ u=frac12left(r+frac1rright)cosvarphi,quad v=frac12left(r-frac1rright)sinvarphi. $$
Рассмотрим две упомянутые выше области $|z| 1$.
В области $|z| 0$ функция Жуковского отобразит на нижнюю полуплоскость $mathfrak w 0$.
Рассмотрим теперь в области $|z|>1$ окружности $|z|=r$, где $1 1$ на всю плоскость $w$ с разрезом вдоль вещественной оси от точки $w=-1$ до точки $w=1$. При этом верхний полукруг отображается на верхнюю полуплоскость, а нижний полукруг — на нижнюю полуплоскость.
Обратная к функции Жуковского функция $$ w=z+sqrt $$ двузначна, что обусловлено двузначностью квадратного корня. Каждую точку $z$ она отображает в две точки $w_1$ и $w_2$, связанные условием $w_1w_2=1$. Легко показать, что точки $z=-1$ и $z=1$ будут точками разветвления этой функции. Таким образом, в любой области, не содержащей замкнутых кривых, обходящих лишь одну из этих точек, можно выделить две однозначные ветви обратной функции. Этому условию, в частности, удовлетворяет вся плоскость $z$ с разрезом вдоль отрезка $[-1,1]$ вещественной оси. Ветви обратной функции однолистно отображают плоскость $z$ с указанным разрезом либо на круг $|w| 1$ и аналитичны.
Видео:Конформные отображения с помощью функции ЖуковскогоСкачать

Тригонометрические функции
Видео:Конформные отображения с помощью степенной функцииСкачать

Теорема Римана. Основные принципы конформных отображений
Теорема 1 (Римана).
Всякую односвязную область $D$ комплексной плоскости $z$, граница которой состоит более чем из одной точки, можно конформно отобразить на внутренность единичного круга $|w| tfkp/chapter3.txt · Последние изменения: 2021/11/02 19:39 — nvr
Видео:Конформные отображения с помощью показательной и логарифмической функцийСкачать

Конформные отображения. Примеры
Пример 5.7
Найти конформное отображение круга |z| с разрезом по отрезку от точки z = 0 до точки z = −i на единичный круг |
Тут не удастся обойтись одной дробно-линейной функцией, иначе внутренность круга обязательно отобразилась бы во внутренность круга безо всяких разрезов.
Шаг 1
Поворот и перевод круга с разрезом в полукруг.
Во-первых, заметим, что круг с разрезом является «почти» двуугольником. В самом деле, границы этой фигуры есть дуги окружностей (одна из которых бесконечного радиуса). Но у этой фигуры, в отличие от двуугольников, во-первых, вершины совпадают z1 = z2 = −i , и, во-вторых, помимо углов при вершинах есть угол в 2π в середине «стороны», состоящей из двух отрезков [0, i] .
Чтобы «выпрямить» эту строну, уменьшим угол в точке z = 0 , равный 2π , в два раза при помощи операции извлечения квадратного корня, а чтобы «выпрямленная» сторона легла на ось Ox , совершим предварительный поворот на 

ζ = 

Ветвь корня 
Видео:Отображения множествСкачать

Конформные отображения. Дробно-линейная функция
Видео:Конформные отображения c помощью дробно-линейной функции: отображение по трем точкамСкачать

Конформные отображения. Дробно-линейная функция
Определение 1. Функция вида
где a, b, c, d – комплексные числа, называется дробно-линейной.
Отображение, задаваемое этой функцией, называется дробно- линейным.
Условие ad − bc ≠ 0 означает, что w ≠ const . Функция (1) осуществляет конформное отображение расширенной комплексной плоскости Z на расширенную комплексную плоскость w, так как производная
Для 0 c ≠ предполагаем, что
для c = 0 функция (1) становится линейной, т. е. w = az + b и w(∞) = ∞. Функция
является обратной к функции (1). Она также является дробно-линейной и однозначной на расширенной комплексной плоскости, т. е. здесь функция (1) является однолистной.
Каждое дробно-линейное отображение может быть получено в результате последовательного выполнения трех отображений: линейного, отображения w = 1/z и снова линейного отображения.
Дробно-линейные отображения переводят:
1) окружность или прямую в окружность или прямую (круговое свойство);
2) пару точек, симметричных относительно окружности, – в пару то- чек, симметричных относительно образа этой окружности (свойство сохранения симметрии). Здесь «окружность», в частности, может быть прямой, если под последней понимать окружность бесконечного радиуса.
Существует единственное дробно-линейное отображение, которое три разных точки z1, z2, z3 переводит соответственно в три разные точки w1, w2, w3. Это отображение задается формулой
Если одна из точек zk или wk (k =1, 2, 3) является бесконечно удаленной точкой, то в формуле (2) разности, в которые входит zk или wk, требуется заменить единицами.
Существует бесконечно много дробно-линейных отображений, которые заданную окружность γ отображают на заданную окружность Г, причем область D, для которой γ является границей, отображается на одну из областей, для которой Г является границей.
Для обеспечения единственности дробно-линейного отображения достаточно выполнение одного из условий:
1) заданная точка z0 ∈ D отображается в заданную точку w0 ∈ D’, а любая кривая, выходящая из точки z0, поворачивается на заданный угол α w0 = f (z0), α = arg(f ‘(z0));
2) точки z0 ∈ D и z1 ∈ γ отображаются соответственно в заданные точки w0 ∈ D’ и w1 ∈ Γ.
Пример 1. Найти образ окружности, заданной уравнением
x 2 + y 2 + 2x − 4y + 1 = 0,
при отображении w = 1/z.
Решение. На основании кругового свойства дробно-линейного отображения окружность переходит в окружность. Для ее нахождения на заданной окружности x 2 + y 2 + 2x − 4y + 1 = 0, выберем три точки, например: z1 = −1 z2 = 1 + 2i, z3 = −3 + 2i, образами которых при отображении w = 1/z будут точки
Точками w1, w2, w3 однозначно определяется образ данной окружности, уравнение которой:
Для отображения w = 1/z имеем
Выразив отсюда x = x(u, v), y = (u, v) и подставив в уравнение заданной окружности, получим искомый образ (3).
Пример 2. Найти образ области D при отображении 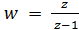
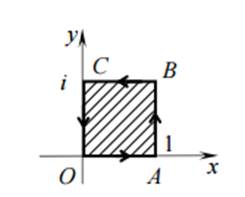
Будем искать образ границы области D (рис. 1).
Сторона OA: y = 0, 0 ≤ x ≤ 1 отображается на отрицательную часть действительной оси (v = 0, − ∞
Рис. 1. Область D
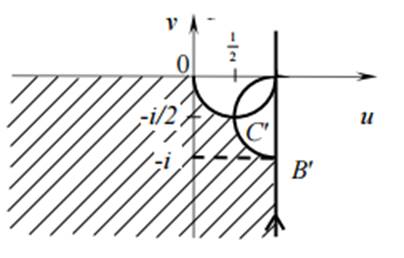
Рис. 2. Образ области D
Сторона AB: x = 1, 0
Сторона BC: y =1, 1 ≥ x ≥ 0, отображается в линию, параметрическое уравнение которой имеет вид
Исключив параметр x, получим
Аналогично образ стороны CO определяется уравнением
В соответствии с принципом соответствия границ образом квадрата будет заштрихованная область на рис. 1.
Пример 3. Найти дробно-линейное отображение, которое точки z1 = 1 и z2 = −1 оставляет неподвижными, а точку z3 = i переводит в точку w3 = 0.
Найти образ полуплоскости Im(z) > 0 при данном отображении.
Решение. По условию имеем три пары соответствующих точек
Применяя формулу (2), получим искомое дробно-линейное отображение 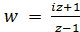
Найдем теперь образ верхней полуплоскости, границей которой является действительная ось. Согласно круговому свойству действительная ось отображается в окружность. Чтобы найти ее, на действительной оси выберем три точки, например: z1 =1, z2 = 0, z3 = −1, образами которых бу- дут точки w1 = 1, w2 = −i, w3 = −1. Они лежат на окружности |w| =1. По принципу соответствия границ получаем, что образом верхней полуплоскости будет область D’= <w, |w|
Пример 4. Найти дробно-линейное отображение, которое круг |z − 4i| u так, что w(4i) = −4, w(2i) = 0.
Решение. Условие задачи определяет две пары соответствующих точек. Третью пару найдем, пользуясь свойством симметрии дробно линейного отображения, согласно которому точки z1 = 4i и z3 = ∞, симметричные относительно окружности |z − 4i| = 2, перейдут в точки w1 = −4 и w3 = − 4i, симметричные относительно прямой u = v . Таким образом, найдена третья пара точек z3 = ∞ и w3 = −4i. По формуле (2) найдем искомое отображение 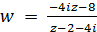
🌟 Видео
Построение областей по заданным условиямСкачать

Конформные отображения c помощью дробно-линейной функции: круговое свойствоСкачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Уравнение окружности (1)Скачать

Власов В. В. - Комплексный анализ (ТФКП) - Конформные отображенияСкачать

Окружности на комплексной плоскостиСкачать
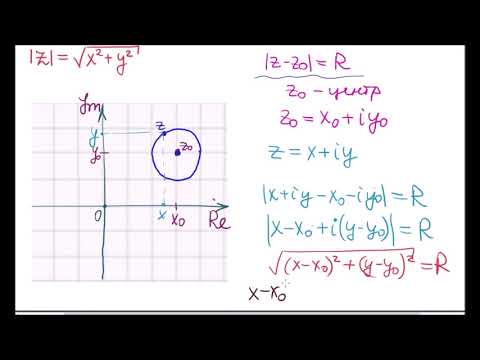
Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Теория функций комплексного переменного 17. Конформные отображения. Дробно-линейные отображенияСкачать

Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

✓ Радиус описанной окружности | ЕГЭ. Задание 1. Математика. Профильный уровень | Борис ТрушинСкачать

лекция 4: примеры конформных отображенийСкачать