Таким образом, изменение сопротивления фаз не влияет на фазные напряжения.
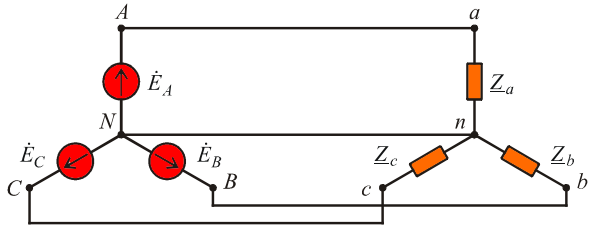
Направления линейных токов от генератора к приемнику примем за положительные (рис. 6-11). Направления фазных токов от А’ к В’, от В’ к С‘ и от С’ к А’ также примем за положительные.
Согласно первому правилу Кирхгофа для мгновенных значений токов для узла А’ можно написать:
Аналогично для узла В’:
Рис. 6-11. Соединение приемников треугольником
Следовательно, мгновенное значение любого линейного тока равно алгебраической разности мгновенных значений токов тех фаз, которые соединены с данным проводом.
Рис. 6-12. Векторная диаграмма при соединении приемников треугольником.
Вектор любого линейного тока находится как разность векторов соответствующих фазных токов:
На рис. 6-12 дана векторная диаграмма для трехфазной цепи при соединении приемников энергии треугольником. На этой диаграмме все векторы проведены из одного начала. На рис. 6-13 дана вторая диаграмма для той же цепи, на которой векторы напряжений образуют треугольник, а вектор каждого фазного тока проведен из одного начала с вектором соответствующего фазного напряжения.
Рис. 6-13. Векторная диаграмма при соединении приемников треугольником.
Если при симметричной системе линейных напряжений нагрузка фаз равномерная, т. е.
то действующие значения фазных токов равны между собой и они сдвинуты по фазам на одинаковые углы от соответствующих напряжений (рис. 6-14) и, следовательно, на углы 120° один относительно другого. Следовательно, фазные токи представляют симметричную систему. Симметричную систему будут представлять и линейные токи (рис. 6-14).
Восстановив перпендикуляр из середины вектора линейного тока, например IА, получим прямоугольный треугольник OHM, из которого следует, что
Таким образом, при соединении приемников треугольником при равномерной нагрузке фаз линейные токи больше фазных в √3 раз.
Кроме того, из той же векторной диаграммы следует, что линейные токи отстают от соответствующих фазных токов на углы 30°.
Рис. 6-14. Векторная диаграмма для цепи, соединенной треугольником при равномерной нагрузке фаз.
При соединении приемников треугольником при равно мерной нагрузке фаз расчет трехфазной цепи сводится к расчету одной фазы.
во фазного напряжения определяются из выражений
Активная мощность одной фазы
Реактивная мощность трех фаз
Полная мощность трехфазной цепи
При неравномерной нагрузке фаз мощность трехфазной цепи о пределяется как сумма мощностей отдельных фаз.
Если приемники энергии соединены звездой и за положительное направление линейных токов вобрано направление от генератора к потребителю, то согласно первому правилу Кирхгофа для нейтральной точки можно написать:
Если приемники энергии соединены треугольником, то сумма линейных токов
Следовательно, при любом способе соединения приемников алгебраическая сумма мгновенных значений линейных токов трехфазной трехпроводной цепи равна нулю.
Поэтому, например, намагничивающая сила трех жил трехфазного кабеля равна нулю и, следовательно, не происходит намагничивания стальной брони кабеля, применяемой для защиты от механических повреждений.
- ВКЛЮЧЕНИЕ ПРИЕМНИКОВ ЭНЕРГИИ В СЕТЬ ТРЕХФАЗНОГО ТОКА
- Похожие страницы:
- Leave a Comment
- Соединение потребителей электрической энергии в треугольник
- Симметричная нагрузка при соединении приемников треугольником
- Пример
- Решение
- Несимметричная нагрузка при соединении приемников треугольником
- Пример
- Решение
- Звезда треугольник — особенности соединений в установках трехфазного тока
- Где применяется соединение звезда и треугольник
- Звезда, треугольник — определения
- Трансформация напряжений при помощи комбинаций звезда и треугольник
- Подключение двигателя звездой или треугольником
- 🎥 Видео
Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

ВКЛЮЧЕНИЕ ПРИЕМНИКОВ ЭНЕРГИИ В СЕТЬ ТРЕХФАЗНОГО ТОКА
Электрические лампы изготовляются на номинальные напряжения 127 и 220 в, а трехфазные электродвигатели на номинальные фазные напряжения 127, 220 и 380 в и выше.
Способ включения приемника в сеть трехфазного тока зависит от линейного напряжения сети и от номинального напряжения приемника.
Лампы с номинальным напряжением 127 в включаются треугольником при линейном напряжении сети 127 в и звездой с нейтральным проводом при линейном напряжений сета 220 в. Лампы с номинальным напряжением 220 в включаются треугольником в сеть с линейным напряжением 220 в и звездой с нейтральным проводом в сеть с линейным напряжением 380 в.
Трехфазный электродвигатель включается треугольником в сеть, линейное напряжение которой равно номинальному фазному напряжению электродвигателя. Если линейное напряжение сети превышает в √3 раз номинальное фазное напряжение электродвигателя, то он включается звездой.
Статья на тему Соединение приемников энергии треугольником
Похожие страницы:
Понравилась статья поделись ей
Leave a Comment
Для отправки комментария вам необходимо авторизоваться.
Видео:Соединение трехфазных цепей звездой и треугольникомСкачать

Соединение потребителей электрической энергии в треугольник
При соединении фаз электроприемников в треугольник каждая фаза будет подключена к двум линейным проводам, как показано на рисунке ниже:
Поэтому при таком типе соединения, обратно звезде, независимо от характера и значения сопротивления приемника каждое фазное напряжение будет равно линейному, то есть UФ = UЛ. Если не брать во внимание сопротивления фазных проводов, то можно предположить, что напряжения источника и приемника электрической энергии равны.
На основании приведенной выше схемы и формулы можно сделать вывод, что соединение фаз приемников электрической энергии в треугольник следует применять тогда, когда каждая фаза трехфазного или двухфазного потребителя электрической энергии рассчитана на линейное напряжение сети.
В отличии от соединения звездой, где фазные и линейные токи равны, при соединении треугольником они равны не будут. Применив первый закон Кирхгофа к узловым точкам a, b, c получим соотношение между фазными и линейными токами:
Имея векторы фазных токов, используя данное соотношение, не трудно построить векторы линейных токов.
Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Симметричная нагрузка при соединении приемников треугольником
В отношении любой фазы можно применять формулы, которые справедливы для однофазных цепей:
Очевидно, что при симметричной нагрузке:
Векторная диаграмма фазных (линейных) напряжений и токов при активно-индуктивной симметричной нагрузке показана ниже:
В соответствии с формулой (1) были построены векторы линейных токов. Также стоит обратить внимание на то, что при построении векторных диаграмм для соединения треугольник вектор линейного напряжения Uab принято направлять вертикально вверх.
Векторы линейных токов часто изображают соединяющими векторы фазных токов, как это показано на рисунке b):
На основании данной векторной диаграммы можно записать: 

Пример
Трехфазная сеть имеет линейное напряжение UЛ = 220 В. К ней необходимо подключить трехфазный электроприемник с фазным напряжением в 220 В и содержащим последовательно подключенные активное rф = 8,65 Ом и индуктивное xф = 5 Ом сопротивления.
Решение
Поскольку линейные и фазные напряжения в этом случае будут равны, то выбираем способ соединения обмоток потребителя в треугольник.
Линейные и фазные токи, а также полные сопротивления фаз будут равны:
Активная, реактивная и полная мощности электроприемника любой фазы будут равны:
Векторные диаграммы приведены выше.
Видео:Трёхфазный переменный ток. Соединение "звезда" и "треугольник"Скачать

Несимметричная нагрузка при соединении приемников треугольником
В случае несимметричного сопротивления фаз, как и при соединении в звезду, для подключения к сети электроприемники разбивают на три примерно одинаковые по мощности группы. Подключение каждой группы производится к двум фазным проводом, у которых есть отличия по фазе:
В пределах каждой группы подключение приемников производится параллельно.
После замены сопротивления нескольких приемников в одной фазе на одно эквивалентное получим такую схему:
Углы сдвига между напряжением и током, мощности и фазные токи можно найти из формулы (2). В случае несимметричной нагрузки (в нашем случае схема выше) фазные мощности, токи, а также углы сдвига (cos φ) не будут равны. Векторная диаграмма для случая, когда фаза ab имеет активную нагрузку, bc – активно-индуктивную, ca – активно-емкостную, показана ниже:
Для определения суммарной мощности всех фаз нужно применять выражение:
Пример
Дана несимметричная электрическая цепь, включенная по схеме выше, с параметрами: UЛ = 220 В, rab = 40 Ом, xLbc = 10 Ом, rbс = 17,3 Ом, xcа = 5 Ом, rCcа = 8,65 Ом. Нужно определить линейные и фазные токи, а также мощности.
Решение
Воспользовавшись выражением для определения комплексных значений получим:
Комплексные значения полных сопротивлений фаз: Zab = 40 Ом, Zbс = 17,3 + j10 Ом, Zbс = 8,65 – j5 Ом.
Комплексные и действующие значения линейных и фазных токов:
Дольше можно проводить расчеты, не прибегая к комплексному методу:
Общие активные и реактивные мощности:
Углы сдвига между токами и напряжениями:
Векторная диаграмма для несимметричного треугольника приводилась выше.
Видео:Последовательное и Параллельное Соединение Проводников // Физика 8 классСкачать

Звезда треугольник — особенности соединений в установках трехфазного тока
Звезда и треугольник — это основные виды соединений в установках трехфазного тока. Каждая схема обладает присущими только ей свойствами, и важно правильно ее применять или комбинировать.
Данный обзор ориентирован в первую очередь на широкую аудиторию, которая может не знать терминологии, особенностей расчетов, векторов и прочей узкоспециализированной информации. Да и ни к чему она, если нет понимания. А ретрансляция учебников и прочей электротехнической литературы без нормального пояснения — путь в никуда. Поэтому постараемся по возможности простыми словами рассмотреть основные особенности использования схем звезда и треугольник.
Видео:Этому не учат, а стоило бы. Чем отличается звезда от треугольника? #звезда #треугольник #двигательСкачать

Где применяется соединение звезда и треугольник
Если проанализировать поисковую выдачу, то окажется, что чаще всего люди ищут информацию о схемах звезда и треугольник в контексте подключения асинхронного трехфазного двигателя. Естественно на бытовом уровне это наиболее частый случай применения той или иной схемы. И, естественно, особенности применения той или иной схемы при подключении трехфазного потребителя мы рассмотрим. Но прежде хотелось бы осветить не менее важное применение комбинаций звезды и треугольника при распределении электроэнергии от электростанции через трансформаторы к потребителям.
Казалось бы, зачем нам знать особенности трансформации электроэнергии? Однако, тема довольно-таки интересная, сложная и мало освещенная. Ведь все мы знаем, что электроэнергия вырабатывается на электростанции генераторами, трансформируется и поступает в наши дома. И если с последним звеном все более или менее понятно. То о первых двух звеньях информация чаще попадается расплывчатая, иногда противоречивая или сложная для восприятия. Поэтому рассмотрим простое объяснение трансформации электроэнергии через комбинации звезда-треугольник, треугольник-звезда. Но прежде приведем определения этих способов соединения.
Видео:Трехфазные цепи. Схема соединения "ЗВЕЗДА"Скачать

Звезда, треугольник — определения
В зависимости от способа соединения обмоток генератора и нагрузки различают соединения звездой и треугольником. Каждая фазная обмотка генератора имеет два вывода, которые условно называют началом и концом. За начало обмотки принимается тот вывод, к которому направлена положительная ЭДС.
При соединении звездой концы всех фаз генератора соединяют в один узел. Его называют нейтральным узлом или нейтральной точкой. Нейтральные точки генератора и нагрузки часто соединяют нейтральным (нулевым) проводом. Остальные провода, соединяющие обмотки генератора с приемником, называют линейными.
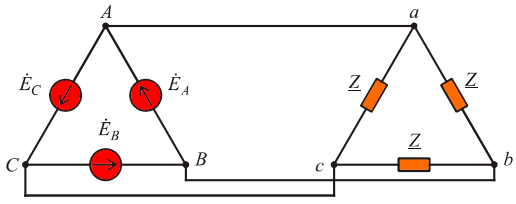
При соединении треугольником начало одной фазной обмотки соединяют с концом следующей так, чтобы три обмотки образовали замкнутый треугольник.
На практике используют различные комбинации соединения фаз генератора и нагрузки: звезда-звезда, звезда-треугольник, треугольник-треугольник. Есть и комбинации с зигзагом, но в данном обзоре мы из затрагивать не будем.
Напряжения и токи в фазах генератора и нагрузки называют фазными и обозначают Uф, Ia. Напряжения между линейными проводами и токи в них называют линейными и обозначают Uл, Iл. Из рассмотренных выше схем следует, что при соединении звездой Iл = Iф, а при соединении треугольником Uл = Uф.
Если обмотки источника питания 220 Вольт соединены треугольником, соответственно фазные и линейные напряжения равны 220 Вольт. Соотношения же между линейными и фазными напряжениями при соединении звездой уже иные. Найти их можно при помощи векторной диаграммы или методом анализа синусоид трех фаз, как показано в следующем ролике:
Расчет линейного напряжения по векторам сводиться к анализу равнобедренного треугольника с углами при основании 30°. Также можно рассчитать разность векторов через комплексные числа. Подробно на данных способах останавливаться не будем. Отметим лишь следствие — при соединении звездой линейное напряжение Uл = √3 × Uф (380 = √3 × 220).
Видео:Соединение треугольникомСкачать

Трансформация напряжений при помощи комбинаций звезда и треугольник
При мощности генератора электростанции 500 МВт и напряжении 10 кВ сила тока в проводах составит 50 тысяч ампер. При передаче на большие расстояния провода, как нагрузка, имеют значительное сопротивление. Следовательно, большая часть тока будет уходить впустую на разогрев проводов. Чтобы минимизировать потери при транспортировке электроэнергии единственный действенный способ — увеличение напряжения, что приведет к снижению силы тока. А без распределительных трансформаторов (повышающих и понижающих) этого сделать нельзя.
Сейчас подробно останавливаться на принципе работы трансформатора не будем. Нас больше интересует особенность соединения его обмоток звездой или треугольником.
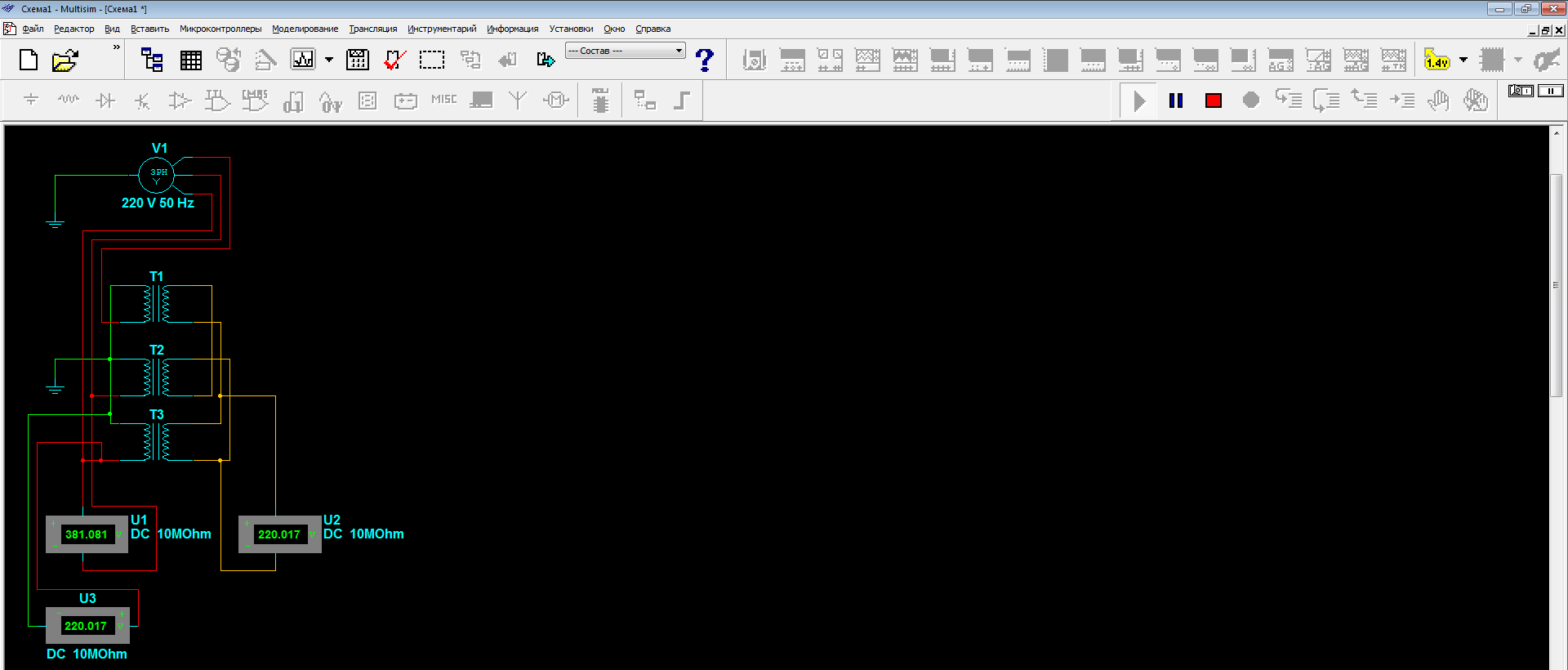
Моделировать будем в программе Multisim. А начнем отрисовку схемы с трехфазного генератора, обмотки которого соединены в звезду. Заземлим точку соединения обмоток. На этом этапе отметим, что несмотря на то, что генераторы на электростанциях вырабатывают напряжения в тысячи вольт и на всем пути трансформируют его увеличивая и уменьшая, мы возьмем генератор, вырабатывающий понятные нам 220 Вольт. Также не стоит сравнивать приведенные здесь схемы с реальной системой, так как путь от электростанции до потребителя намного сложнее.
Теперь добавим трансформатор. Точнее соберем его из трех трансформаторов таким образом, чтобы первичная обмотка была соединена в звезду, а вторичная — в треугольник. Повышать напряжение не будем, но посмотрим, какая трансформация произошла при соединении обмоток трансформатора по схеме звезда-треугольник.
При переключении со звезды в треугольник обмоток генераторов или вторичных обмоток трансформаторов происходит следующее:
- Напряжение в сети понижается в 1,73 раза. В нашем случае линейное напряжение понижается с 380 до 220 Вольт.
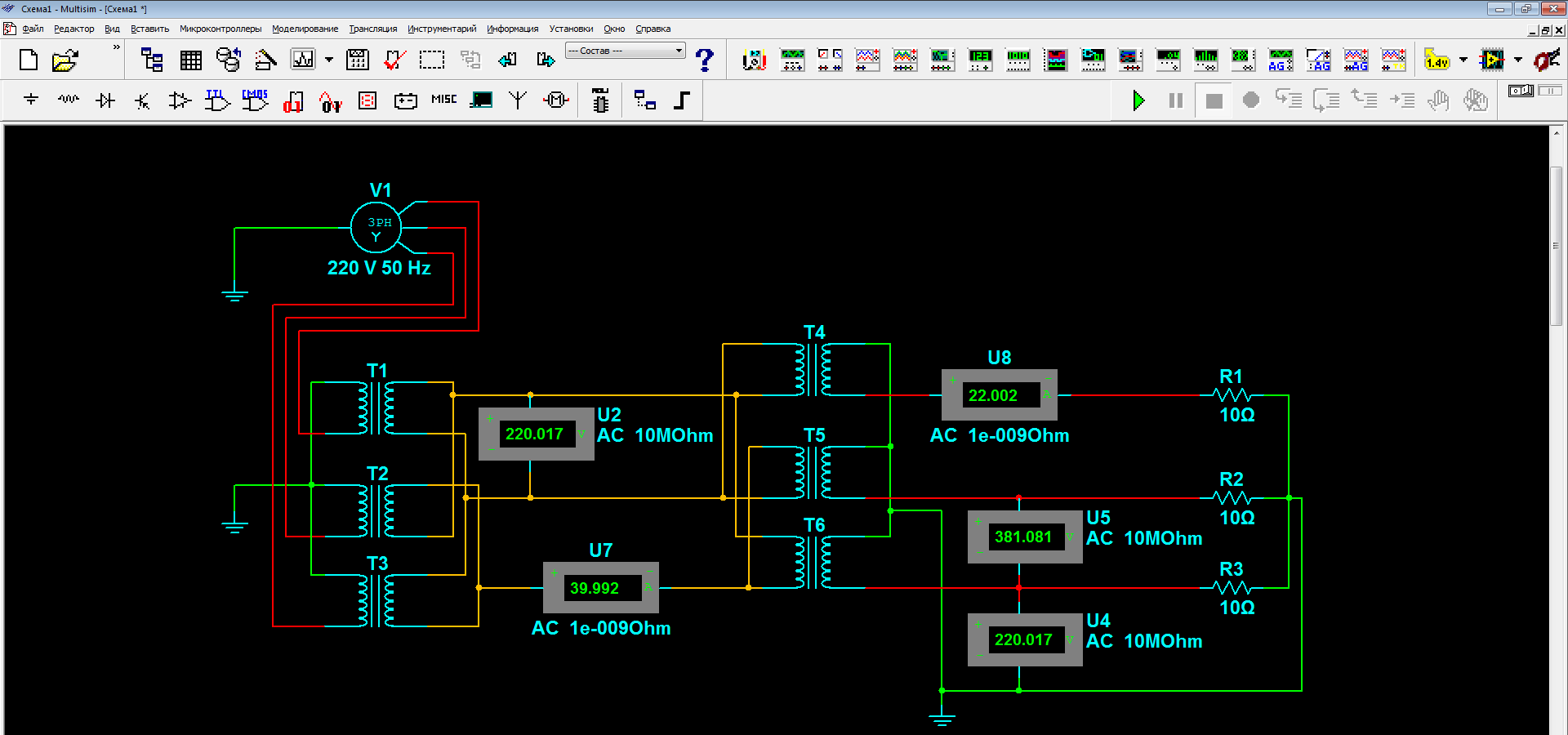
- Мощность генератора и трансформатора остается такой же. А все потому что напряжение каждой фазной обмотки остается таким же и ток в каждой фазной обмотке такой же, хотя ток в линейных проводах возрастает в 1,73 раза. Это мы покажем чуть позже, когда замкнем цепь через потребителей. Но прежде добавим в нашу схему еще один трансформатор со схемой треугольник звезда и подключим к нему нагрузку.
При переключении обмоток генераторов или вторичных обмоток трансформаторов с треугольника в звезду происходят обратные явления:
- Линейное напряжение в сети повышается в 1,73 раза. В нашем случае с 220 до 380 Вольт.
- Токи в фазных обмотках остаются теми же, токи в линейных проводах уменьшаются в 1,73 раза.
Теперь разберемся в причинах трансформаций простыми словами без использования векторов. Для этого рассмотрим движение свободных электронов в цепи и проанализируем потенциалы в конкретный момент времени. Такого объяснения вы наверно нигде не увидите, но оно, возможно, наиболее простое для восприятия.
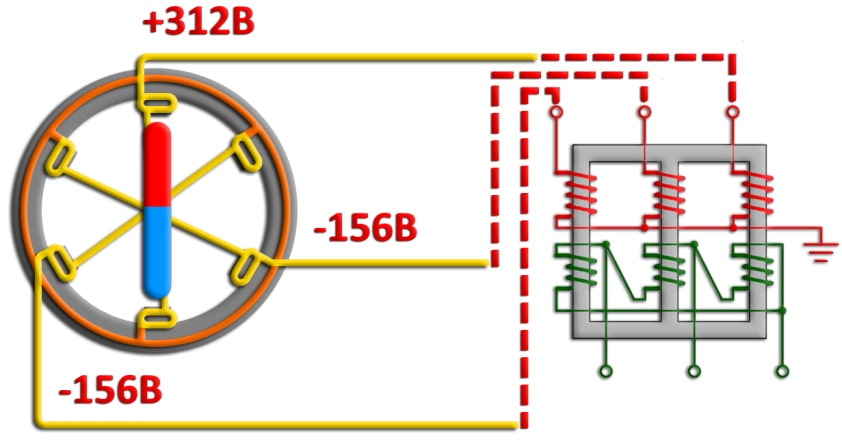
Первое в нашей цепи — это генератор. Упрощенно в нем имеется три обмотки статора, смещенные на 120° относительно друг друга. При вращении ротора в обмотках статора возникает периодически изменяющаяся ЭДС с амплитудой приблизительно 312 Вольт. Это амплитудное значение напряжения, и переходить от него к действующему не будем. В момент, когда напряжение на одном из выводов генератора +312 Вольт, на двух других по -156 Вольт. Остановимся на этом моменте и перейдем к напряжениям обмоток трансформатора.
Напряжения в рассматриваемый момент времени как на первичной обмотке, так и на вторичной обмотке соответствуют выделенным выше +312, -156, -156 Вольтам. Так почему же токи в линейных проводах, отходящих от обмоток треугольника увеличиваются в корень из трех раз, а линейное напряжение во столько же раз уменьшается? Весь секрет в особенности соединения обмоток в треугольник, и далее мы наглядно продемонстрируем это перейдя к более упрощенной схеме.
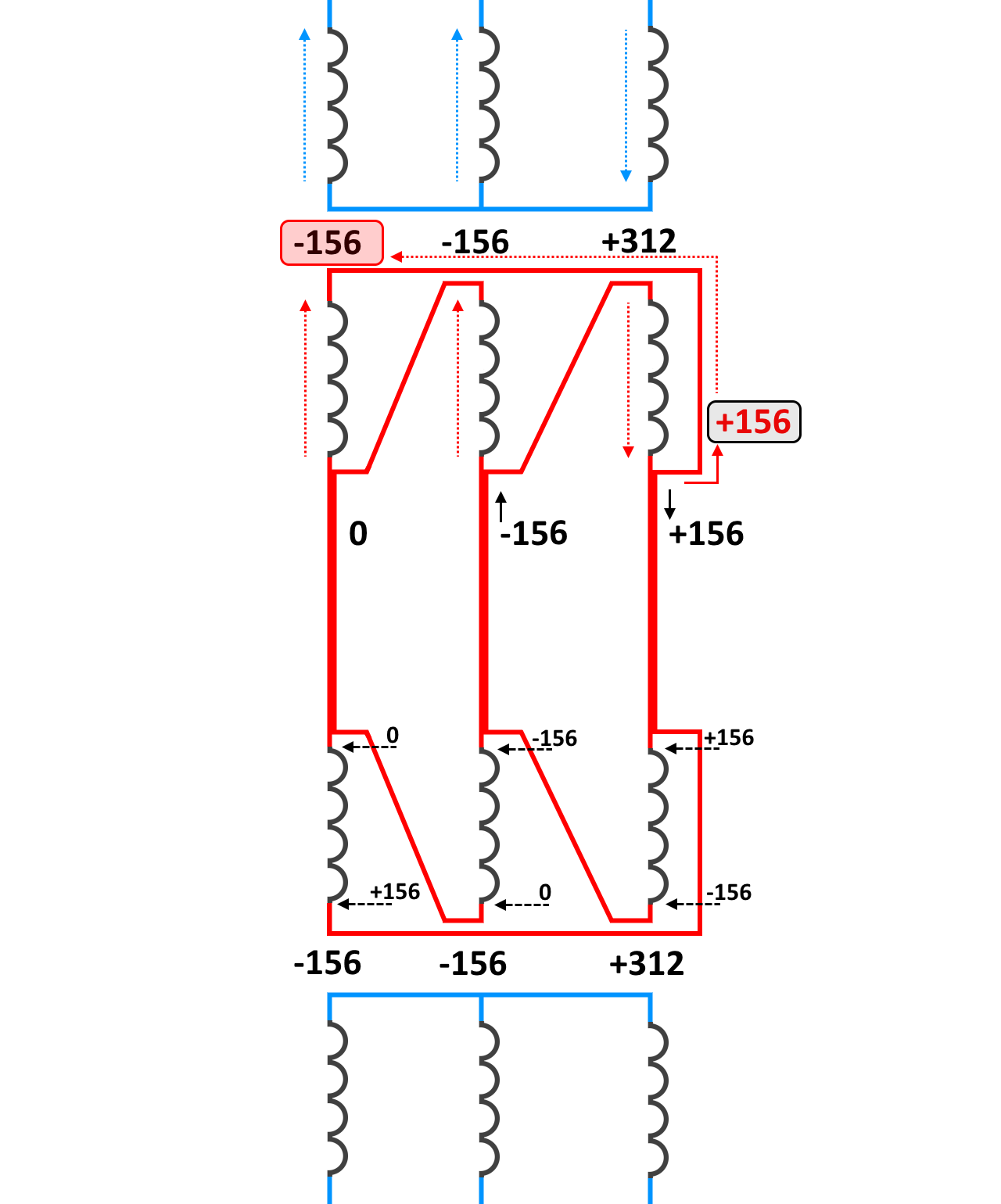
Так как при соединении треугольником начало одной фазной обмотки соединяют с концом следующей, то напряжение обмотки +312 Вольт распределится между обмоткой с напряжением -156 Вольт и выводом. В результате на выводе обмотки с напряжением +312 Вольт будет +156 Вольт, а на выводе обмотки с напряжением -156 Вольт будет 0 Вольт. У нас остается третья обмотка с напряжением -156 Вольт, и на выводе у нее так и останется -156 Вольт. В результате получаем напряжения на выходе в рассмотренный нами момент +156, -156, 0 Вольт (а было +312, -156, -156 Вольт).
Получившееся линейное напряжение +156-(-156) = +312 Вольт (это амплитудное значение). После перевода в действующее значение получим 220 Вольт. Почему не рассматривается 0 Вольт? Нужно понимать что частота 50 Герц ни куда не пропала, и там где ноль, через мгновение будет +156, еще через мгновение -156. И такое чередование будет постоянным. Но вернемся к рассматриваемому моменту времени. С падением линейного напряжения с 380 до 220 Вольт разобрались. Теперь объясним, почему произошло увеличение силы тока. На самом деле все просто. Уменьшив напряжение для передачи первоначальной мощности нам нужно пропорционально увеличить силу тока.
При переходе с треугольника на звезду происходит обратная трансформация. Чтобы это увидеть на схеме, нужно найти напряжения обмоток на втором трансформаторе, подключенном по схеме треугольник звезда. Посчитав разности потенциалов начал и концов обмоток мы вернемся к изначальным +312, -156, -156 Вольт.
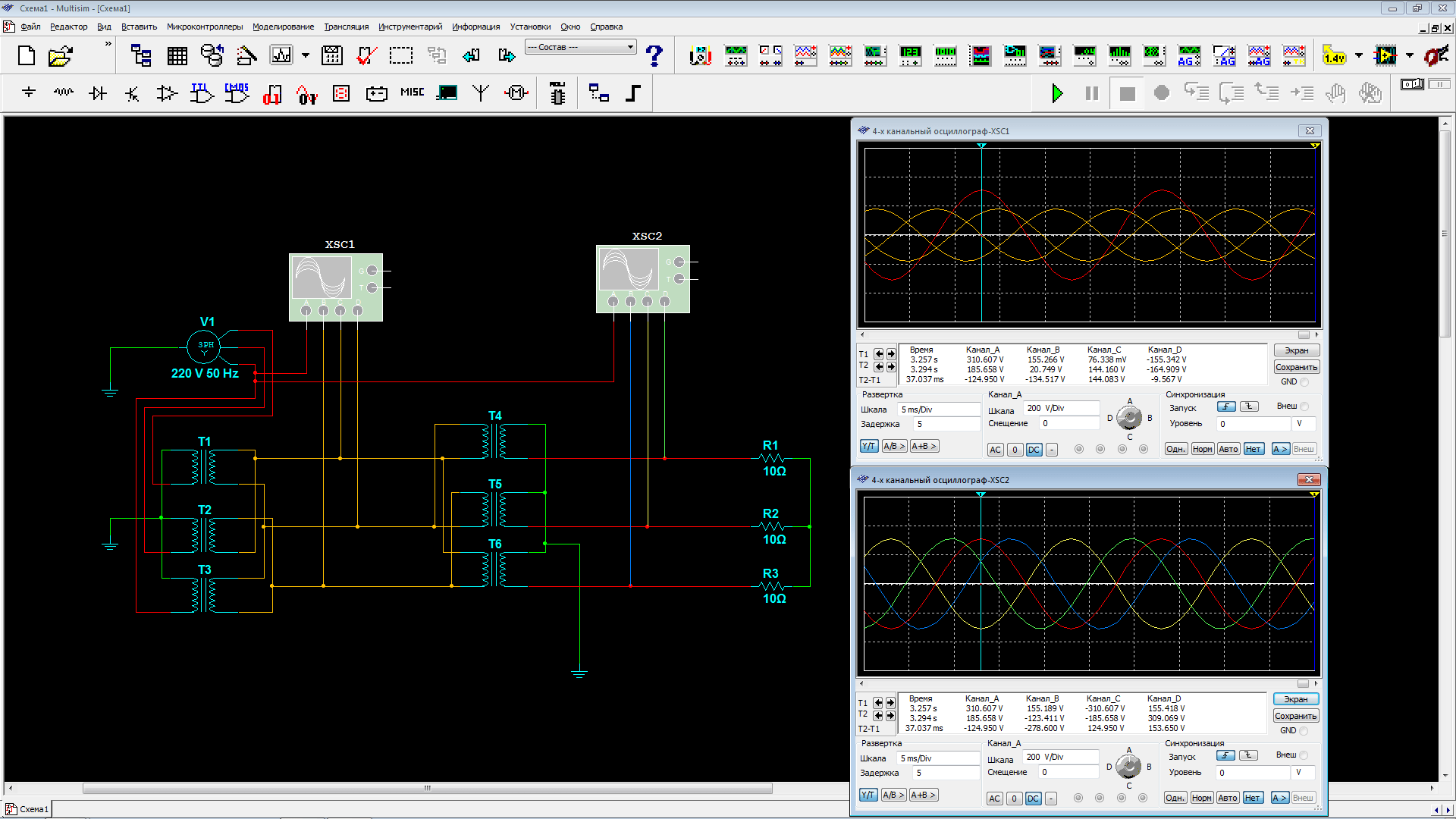
Для того чтобы подтвердить наши расчеты и наглядно увидеть сдвиг фаз вернемся к программе Multisim и подключим к фазам осциллограф.
К выводу A осциллографа xsc1 подключена фаза, идущая от генератора с обмотками по схеме звезда. К остальным трем выводам данного осциллографа подключены фазы после трансформации звезда треугольник. Как видно после трансформации синусоида фазы сместилась на 30°. И если подвести курсор к амплитудному значению ≈ +310 Вольт канала A, то на остальных каналах, относящихся к фазам после трансформации будет приблизительно +155, -155 и 0 Вольт. То есть то же, что мы просчитывали ранее, показал осциллограф.
Для анализа обратной трансформации к выводу A осциллографа xsc2 мы подключили ту же фазу от генератора, а остальные выводы соединили с фазами после трансформатора со схемой треугольник звезда. В результате пропал сдвиг и синусоиды фаз вернули свои амплитуды 312 Вольт. Правда если обратите внимание синусоиды фаз после трансформации отразились зеркально по отношению к синусоидам фаз после генератора. Для того, чтобы отразить обратно, достаточно поменять местами выводы обмоток по схеме звезда.
Как видно применяя различные комбинации «звезды» и «треугольника» с одинаковыми индуктивностями первичных и вторичных обмоток можно от одного напряжения переходить к другому. А для того, чтобы все это наглядно увидеть, достаточно воспользоваться программой для моделирования цифровых и аналоговых электронных схем. В нашем случае моделирование производилось в среде программы Multisim.
Видео:Трехфазные электрические цепи. Соединение треугольникомСкачать

Подключение двигателя звездой или треугольником
После рассмотрения схем соединения обмоток трансформатора, важно не запутаться с напряжениями и токами применительно к асинхронным трехфазным двигателям, подключенным звездой или треугольником. Поэтому лучше сразу абстрагироваться от предыдущих схем.
Начать рассмотрения особенностей подключения асинхронного двигателя нужно с его паспортных данных:
| Номинальная мощность | Pном, кВт |
| Номинальное напряжение (треугольник/звезда) | Uном, В |
| Номинальная частота тока | f, Гц |
| Номинальная частота вращения | nном, об/мин |
| Номинальный КПД | ηном, % |
| Номинальный коэффициент мощности | cosφном, д.е. |
| Кратность максимального момента | Ммакс/Мном |
| Кратность пускового момента | Мпуск/Мном |
И здесь нас интересует номинальное напряжение трехфазного источника электроэнергии, к которому подключается асинхронный двигатель при разном способе соединения фаз обмотки статора.
Если обратить внимание на приведенную выше табличку на корпусе двигателя, то 220/380 В означает, что при соединении фаз обмотки способом «звезда» двигатель подключается к трехфазному источнику напряжением 380 В, а при соединении «треугольником» — 220 В. И здесь главное не запутаться и все правильно понять. 220 Вольт указанные на табличке — это линейное напряжение, а не фазное из розетки. Поэтому такой двигатель нельзя соединять треугольником к трем фазам с линейным напряжением 380 Вольт, которое имеется повсеместно. Необходимо именно линейное напряжение 220 Вольт, которому соответствует фазное напряжение 127 Вольт. При этом, если имеется линейное напряжение 220 Вольт, то рассмотренный выше двигатель можно подключить по схеме звезда, но его мощность упадет в три раза. И дальше мы этот факт подробно разберем.
При соединении обмоток двигателя в звезду линейные токи I и фазные токи Iф равны, а между фазными и линейными напряжениями существует соотношение U = √3 × Uф, откуда Uф = U / √3. Соответственно получим следующие формулы определения мощности:
- Полная S = 3 × Sф = 3 × (U / √3) × I = √3 × U × I.
- Активная P = √3 × U × I × cos φ;
- Реактивная Q = √3 × U × I × sin φ.
При соединении обмоток двигателя в треугольник линейные напряжения U и фазные напряжения Uф равны, а между фазными и линейными токами существует соотношение I = √3 × Iф, откуда Iф = I / √3. Соответственно получим следующие формулы определения мощности:
- Полная S = 3 × Sф = 3 × U × (I / √3) = √3 × U × I.
- Активная P = √3 × U × I × cos φ.
- Реактивная Q = √3 × U × I × sin φ.
Как видно формулы определения мощности при разных способах соединения обмоток одинаковые. И может показаться, что никакой разницы в мощности между звездой и треугольником нет. Так откуда взялось упоминавшееся выше падение мощности в три раза. Весь секрет кроется в соотношениях напряжения и силы тока. И для наглядности просчитаем мощности для уже рассмотренного асинхронного двигателя с маркировкой на табличке треугольник/звезда (220/380 В, 8,3/4,8 А).
Сначала нам нужно подключить обмотки двигателя по схеме треугольник. Для этого потребуется линейное напряжение 220 Вольт. Рассчитаем полную мощность:
Sтреугольник = √3 × U × I = √3 × 220 × 8,3 = 3163 В×А.
Теперь подключим обмотки по схеме звезда. Линейное напряжение остается прежним 220 Вольт. И здесь важно понимать, что по сравнению с указанными на табличке 380 Вольтами для звезды, при линейном напряжении 220 Вольт на каждую фазную обмотку придется в 1,73 (√3) раза более низкое напряжение. Более низкое напряжение приведет к тому, что ток в обмотках уменьшится в 1,73 раза. Соответственно при расчете силу тока 4,8 А нужно будет разделить на √3. Теперь рассчитаем полную мощность:
Sзвезда = √3 × U × I/√3 = √3 × 220 × 4,8/√3 = 1056 В×А.
Как видно из примера, при пересоединении электродвигателя с треугольника в звезду и питании его от той же электросети мощность, развиваемая электродвигателем, снижается в 3 раза. И наоборот, если электродвигатель переключить со звезды в треугольник, мощность резко возрастает, но при этом электродвигатель, если он не предназначен для работы при данном напряжении и соединении в треугольник, быстро выйдет из строя. Для того чтобы добиться одинаковой мощности, линейное напряжение при подключении звездой должно быть в √3 раз больше линейного напряжения, рассчитанного для треугольника, что и указывается в паспортных данных электродвигателя.
🎥 Видео
Звезда,треугольник соединение сопротивленийСкачать
Трехфазные электрические цепи │Теория ч. 1Скачать

Мощность трехфазного напряжении при подключении нагрузки звездой и треугольникомСкачать

Соединение звезда и треугольник. Различие между нимиСкачать
Расчет Трехфазной цепи Без комплексных чисел. Соединение треугольникомСкачать

Схемы и группы соединений обмоток силовых трансформаторовСкачать

Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Лекция 25. Преобразование звезды в треугольник.Скачать

Урок 11. ВСЕ Способы соединения резисторовСкачать

Что такое звезда и треугольник в трансформаторе?Скачать

Последовательное соединение - как это работает?Скачать