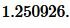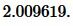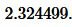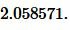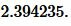Боковые стороны равнобедренного треугольника равны 30, основание равно 36. Найдите радиус описанной окружности этого треугольника.
Найдем площадь треугольника по формуле Герона:
Далее по формуле имеем:
Приведем решение Александры Саяпиной.
Пусть AB — основание равнобедренного треугольника. По теореме косинусов найдем косинус угла A:
следовательно, Тогда по теореме синусов
откуда
- Основания равнобедренного треугольника равно 36 вписанная окружность
- Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?
- Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
- Основание равнобедренного треугольника равно16см, боковая сторона17см?
- В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см?
- В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности?
- Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности?
- Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см?
- Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
- Основание равнобедренного треугольника равно 18 см?
- Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
- Угол при основании равнобедренного треугольника равен a?
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- 1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- 2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- 3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- 4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- 5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
- Основания равнобедренного треугольника равно 36 вписанная окружность
- Источник задания: Решение 3951. ЕГЭ 2016 Математика, И.В. Ященко. 36 вариантов. Ответ.
- Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?
- Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
- Основание равнобедренного треугольника равно16см, боковая сторона17см?
- В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см?
- В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности?
- Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности?
- Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см?
- Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
- Основание равнобедренного треугольника равно 18 см?
- Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
- Угол при основании равнобедренного треугольника равен a?
Видео:№158. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой сторонеСкачать

Основания равнобедренного треугольника равно 36 вписанная окружность
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?
Геометрия | 5 — 9 классы
Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности.
Найдём высоту равнобедренного треугольника, она является медианой, поэтому делит основание пополам 36 : 2 = 18.
Пифагора h = корень из30 ^ 2 — 18 ^ 2 = корень из576 = 24, найдём площадь этого треугольника S = 1 / 2 * 36 * 24 = 432см ^ 2, эту же площадь можно вычислить через радиус описанной окружности S = abc : (4R) отсюда R = abc : (4S) = 30 * 30 * 36 : (4 * 432) = 18.
75 эту же площадь можно вычислить через радиус вписанной окружности S = 1 / 2Pr поэтому
r = 2S : P = 2 * 432 : (30 + 30 + 36) = 9
ответ 9см и 18, 75см.
Видео:Геометрия Найдите боковую сторону равнобедренного треугольника площадь которого равна 36 см2 а уголСкачать

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.
Найти радиус вписанной и описанной окружности.
Видео:2044 сторона правильного треугольника равна 36 корней из 3Скачать

Основание равнобедренного треугольника равно16см, боковая сторона17см?
Основание равнобедренного треугольника равно16см, боковая сторона17см.
Найти радиус вписанной и описанной окружности.
Видео:Периметр равнобедренного треугольника равен 35 см, а его основание больше боковой стороны в 1,5 разаСкачать

В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см?
В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см.
Найти радиус вписанной и описанной окружности.
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности?
В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности.
Видео:№ 108 - Геометрия 7-9 класс АтанасянСкачать

Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности?
Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности.
Видео:Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см?
Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см.
Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Видео:Геометрия Длина основания треугольника равна 36 см. Прямая, параллельная основанию, делит площадьСкачать

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.
Найти радиус вписанной и описанной окружности.
Видео:Сможешь найти основание? Задача про медиану равнобедренного треугольникаСкачать
Основание равнобедренного треугольника равно 18 см?
Основание равнобедренного треугольника равно 18 см.
Боковая сторона равна 15 см.
Найти радиусы вписанной треугольник и описанной около треугольника окружности.
Видео:Найдите площадь треугольника на рисунке, если площадь четырёхугольника равна 36 ★ Как решать?Скачать
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.
Найти радиус вписанной и радиус описанной окружности.
Видео:Задача 6 №27589 ЕГЭ по математике. Урок 57Скачать

Угол при основании равнобедренного треугольника равен a?
Угол при основании равнобедренного треугольника равен a.
Радиус вписанной окружности равен r.
Найти стороны треугольника и радиус описанной окружности.
Вопрос Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Диагонали прямоугольника равны, при пересечении делятся пополам и со сторонами образуют равнобедренные треугольники. Углы при основании равнобедренного треугольника равны. ∠СОD = ∠АОВ = 50° — вертикальные. Сумма углов треугольника 180°. Углы при ..
По т. Пифагора боковая сторона равняется 10 = √(6² + 8²) = √100. S = 0. 5 * 12 * 8 = 48 ; площадь через боковую сторону S = 10 * h * 0. 5 = 5h. 48 = 5h ; h = 48 / 5 = 9. 6.
34вот ответ и все я тоже такую задачу решал.
Ну я так думаю , Т. К. радиус равен 25, значит диаметр 25 * 2 = 50 это будет сторона АВ Мы знаем что АВ = 50 , ВС = 48 , найти АС , По теореме Пифагора АВ ^ 2 = АС ^ 2 + CВ ^ 2 50 ^ 2 = АС ^ 2 + 48 ^ 2 2500 = АС ^ 2 + 2304 АС ^ 2 = 2500 — 2304 АС ^ ..
Делай через уравнение : 1)x + x + 20 = 180 (смежные) 2)2x = 160 3)x = 80 4)x + 20 = 80 + 20 = 100.
Коэффициент пропорциональности = frac отношение площадей : frac = frac S (2) = 8 / (4 / 25) = 2 * 25 = 50 см ^ 2.
Еорема 1. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.
Скажи какой учебник какой номер вопроса, автора.
Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:36 ГРАДУСОВ + ЛЮБОВЬ СОФЬИ КОВАЛЕВСКОЙ!Скачать

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
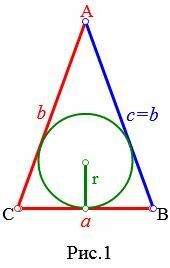 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
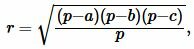 | (1) |
где полупериметр p вычисляется из формулы:
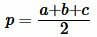 . . | (2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac ) ( small =frac , ) | (3) |
| ( small p-a=frac -a ) ( small =frac , ) | (4) |
| ( small p-b=p-c=frac -b ) ( small =frac . ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
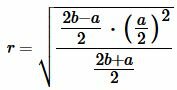 , , |
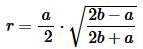 . . | (6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
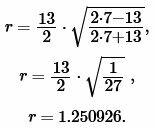 |
Ответ:
Видео:Геометрия Основание равнобедренного треугольника равно a а противолежащий ему угол равен α НайдитеСкачать

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
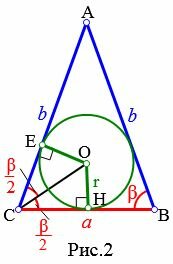 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac . ) Для прямоугольного треугольника OCH можно записать:
| ( small frac =frac >=mathrm frac .) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac cdot mathrm frac .) | (8) |
| ( small r=frac cdot frac .) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
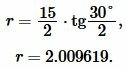 |
Ответ:
Видео:№240. Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см,Скачать
3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
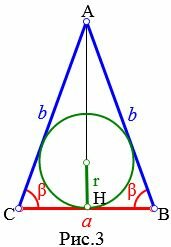 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| ( small frac =frac > = cos beta .) |
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=frac cdot mathrm frac =frac cdot mathrm frac ) ( small =b cos beta cdot mathrm frac ) |
| ( small r=b cdot cos beta cdot mathrm frac ) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac ) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
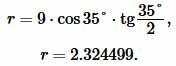 |
Ответ:
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
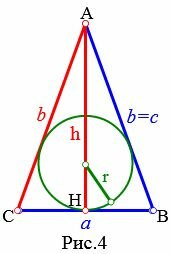
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
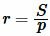 , , | (13) |
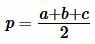 | (14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| ( small left( frac right)^2=b^2-h^2 ) |
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac ) ( small =frac ) ( small =frac +b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac ) ( small =frac > > ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
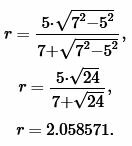 |
Ответ:
Видео:2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
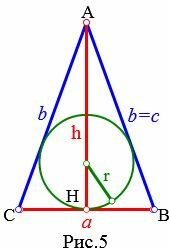
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
 |
Из формулы (15) найдем b:
| ( small b^2-h^2=left( frac right)^2 ) |
| ( small b^2= frac +h^2 ) |
| ( small b= frac cdot sqrt ) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=frac > >) ( small =frac +h^2-h^2>> cdot sqrt + sqrt +h^2-h^2>>) ( small = large frac > cdot sqrt +frac >) |
| ( small r=large frac >) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
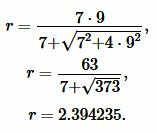 |
Ответ:
Видео:№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

Основания равнобедренного треугольника равно 36 вписанная окружность
Видео:Найти основание равнобедренного треугольника Д353Скачать

Источник задания: Решение 3951. ЕГЭ 2016 Математика, И.В. Ященко. 36 вариантов. Ответ.
Задание 16. Основание и боковая сторона равнобедренного треугольника равны 34 и 49 соответственно.
а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.
б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.
а) Пусть О — центр окружности, вписанной в треугольник ABC со сторонами АВ = АС = 49, ВС = 34, АН — высота треугольника, точки М и N — середины сторон АВ и АС соответственно, K — точка пересечения АН и MN, p — полупериметр треугольника ABC. Поскольку MN — средняя линия равнобедренного треугольника, точка K — общая середина MN и АН.
Из прямоугольного треугольника АВН находим, что

значит, 
Пусть r — радиус вписанной окружности треугольника ABC. Тогда

а диаметр вписанной окружности равен 


Следовательно, вписанная окружность пересекает среднюю линию MN треугольника.
б) Пусть вписанная окружность касается сторон АВ и АС в точках D и Е соответственно, а средняя линия MN пересекает эту окружность в точках Р и Q (Р между М и Q). Тогда
По теореме о касательной и секущей 
то 
Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?
Геометрия | 5 — 9 классы
Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности.
Найдём высоту равнобедренного треугольника, она является медианой, поэтому делит основание пополам 36 : 2 = 18.
Пифагора h = корень из30 ^ 2 — 18 ^ 2 = корень из576 = 24, найдём площадь этого треугольника S = 1 / 2 * 36 * 24 = 432см ^ 2, эту же площадь можно вычислить через радиус описанной окружности S = abc : (4R) отсюда R = abc : (4S) = 30 * 30 * 36 : (4 * 432) = 18.
75 эту же площадь можно вычислить через радиус вписанной окружности S = 1 / 2Pr поэтому
r = 2S : P = 2 * 432 : (30 + 30 + 36) = 9
ответ 9см и 18, 75см.
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.
Найти радиус вписанной и описанной окружности.
Основание равнобедренного треугольника равно16см, боковая сторона17см?
Основание равнобедренного треугольника равно16см, боковая сторона17см.
Найти радиус вписанной и описанной окружности.
В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см?
В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см.
Найти радиус вписанной и описанной окружности.
В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности?
В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности.
Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности?
Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности.
Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см?
Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см.
Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.
Найти радиус вписанной и описанной окружности.
Основание равнобедренного треугольника равно 18 см?
Основание равнобедренного треугольника равно 18 см.
Боковая сторона равна 15 см.
Найти радиусы вписанной треугольник и описанной около треугольника окружности.
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?
Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.
Найти радиус вписанной и радиус описанной окружности.
Угол при основании равнобедренного треугольника равен a?
Угол при основании равнобедренного треугольника равен a.
Радиус вписанной окружности равен r.
Найти стороны треугольника и радиус описанной окружности.
Вопрос Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
1) 6 : 2 = 3 см — середина АВ и середина СD , так как они равны. 6 см + 3 см + 3 см = 12 см Ответ : 12 см 2) Не знаю как решать , извини. 3) Возьмем АВ за х AM = MB = x 2 Тогда MN = BN = MB 2 = x 4 AM : MN = x 2 : x 4 = 2 : 1 BN : AM = x ..
SΔ = (a * ha) / 2 SΔ = (14 * 6) / 2 = 42 см².
По твоему чертежу, но без окружности : А 0 — центр окружности I А0 — радиус I 0В — радиус I 0С — радиус I0___________C ∠А0С = ∠В0С = 90° I Соедини· А и· С I Получим равнобедренныйΔ А0С I А0 = 0С (это радиусы) I В равнобедренномΔ углы при основании B ..
1)х + х + 160 = 180 2х = 20 х = 10 2)160 + 10 = 170.
Так как треугольник авс равнобедренный ав = вс то и ам = ск тогда треугольник вмк равнобедренный.
Дано : угол АВ, угол АD = 80градусов, угол ВD, угол AC = углуCB (это равенствопоказывает то, что С — биссектриса АВ), уголAD = углуDC. Найти : уголBD Решение : 1) уголAD× 2 = углуAC уголAC = углуCB 80× 2 = 160 — угол CB 2) уголDC + уголCB = углуBD 8..
АС = 50 + 16 = 66 М = АВ / 2 = 50 / 2 = 25 см К = ВС / 2 = 16 / 2 = 8 МК = 66 — 33 = 33 см.
1) а не параллельно b, т. К. угол4 = 180 — 60 = 120градусов (т. К. угол3 и угол4 смежные)угол4 и угол 1 являются накрест лежащими, но они не равны, значит а не параллельна b. 2) угол3 + угол4 = 180градусов, т. К. они односторонние. Пусть угол3 =..
СМ = CN = R. АК + КВ = с, АК = AN, ВК = ВМ. Пусть АК = AN = х, ВК = ВМ = 15 — х. АВ² = АС² + ВС², 15² = (х + 3)² + (15 — х + 3)², 225 = х² + 6х + 9 + 324 — 36х + х², 2х² — 30х + 108 = 0, х² — 15х + 54 = 0, корни квадратного уравнения : х1 = 6 и х2..
Через точку, которая лежит на прямой, можно провести, через неё лишь одну прямую.