Основание равнобедренного треугольника 36

Боковые стороны равнобедренного треугольника равны 30, основание равно 36. Найдите радиус описанной окружности этого треугольника.

Найдем площадь треугольника по формуле Герона:

Далее по формуле имеем:

Приведем решение Александры Саяпиной.

Пусть AB — основание равнобедренного треугольника. По теореме косинусов найдем косинус угла A:

следовательно, Тогда по теореме синусов откуда

Видео:№158. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой сторонеСкачать

Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?

Геометрия | 5 — 9 классы

Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности.

Найдём высоту равнобедренного треугольника, она является медианой, поэтому делит основание пополам 36 : 2 = 18.

Пифагора h = корень из30 ^ 2 — 18 ^ 2 = корень из576 = 24, найдём площадь этого треугольника S = 1 / 2 * 36 * 24 = 432см ^ 2, эту же площадь можно вычислить через радиус описанной окружности S = abc : (4R) отсюда R = abc : (4S) = 30 * 30 * 36 : (4 * 432) = 18.

75 эту же площадь можно вычислить через радиус вписанной окружности S = 1 / 2Pr поэтому

r = 2S : P = 2 * 432 : (30 + 30 + 36) = 9

ответ 9см и 18, 75см.

Видео:Геометрия Найдите боковую сторону равнобедренного треугольника площадь которого равна 36 см2 а уголСкачать

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.

Найти радиус вписанной и описанной окружности.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Основание равнобедренного треугольника равно16см, боковая сторона17см?

Основание равнобедренного треугольника равно16см, боковая сторона17см.

Найти радиус вписанной и описанной окружности.

Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см?

В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см.

Найти радиус вписанной и описанной окружности.

Видео:№ 108 - Геометрия 7-9 класс АтанасянСкачать

В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности?

В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности.

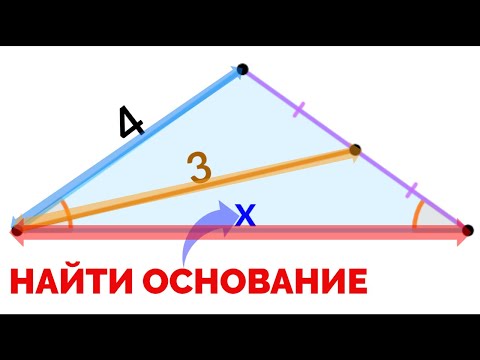
Видео:Сможешь найти основание? Задача про медиану равнобедренного треугольникаСкачать

Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности?

Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности.

Видео:№108. Периметр равнобедренного треугольника ABC с основанием ВС равен 40 см, а периметрСкачать

Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см?

Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см.

Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.

Видео:7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.

Найти радиус вписанной и описанной окружности.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Основание равнобедренного треугольника равно 18 см?

Основание равнобедренного треугольника равно 18 см.

Боковая сторона равна 15 см.

Найти радиусы вписанной треугольник и описанной около треугольника окружности.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.

Найти радиус вписанной и радиус описанной окружности.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Угол при основании равнобедренного треугольника равен a?

Угол при основании равнобедренного треугольника равен a.

Радиус вписанной окружности равен r.

Найти стороны треугольника и радиус описанной окружности.

Вопрос Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Task / 24843118 — — — . — — — . — — — . — — — . — — — 7. ΔBDC

ΔCDA CD / AD = BD / CD⇒CD = x = √(AD * BD) = √(18 * 32) = √(9 * 2 * 2 * 16) = 2 * 3 * 4 = 24. ΔADC

ΔACB AC / AB = AD / AC⇒AC = y = √(AB * AD) = √(18 + 32) * 32) = √(5² * 2² * 4²) = 4..

По правилу треугольки третья сторона треугольника ВС = АС — АВ, а так как АС = а, АВ = b, то ВС = а — b. Если AD — медиана, то ВD = ВС⇒или(а — b) = a — b. По правилу сложения векторов в треугольнике AD = b + 1 / 2a — 1 / 2b = 1 / 2a + 1 / 2b. А ес..

Угол АВС = 80°(по свойству углов)(Противоположные углы ромба равны, соответственно угол ВDС = углу АВС = 80°) Дальше можно составить уравнение : За х, х возьмём углы ВАD И BCD. 80 + 80 + х + х = 360(т. К. сумма всех углов равна 360°) х = 100. Отве..

Вот решение понятно.

А1. 3) А2. 2) А3. 1) А4. 2) В1) ВD = (12 — 10) + 5 = 7 cм.

Я точно не уверен кто я , но я точно знаю что я хочу стать (кем ты хочеше стать? ) например пожарным. Я буду спасать жизни людей).

Соединим середину хорды АВ (точку D) с серединой хорды АС (точка Е). Отрезок DF перпендикулярен АС (расстояние от середины хорды АВ до хорды АС), тогда AF = 3(так как DA = 5см, а DF = 4см), EF = 3см (6 — 3 = 3) а DЕ = 5см. DЕ — средняя линия треуго..

Вписанный угол, опирающийся на диаметр, прямой. BC — диаметр окружности, описанной около треугольника BCC1. BC — диаметр окружности, описанной около треугольника BCB1. Точки B, C, B1, C1 лежат на одной окружности. Угол BCC1 опирается на дугу BC1.

Отрезок это прямая у которой есть начало и есть конец. То есть есть и точка в начале и точка в конце. Она НЕ бесконечная.

Видео:Геометрия 7 класс 36 неделя Повторение Свойства равнобедренного треугольникаСкачать

Основание равнобедренного треугольника равно 36 вписанная окружность касается боковых

Видео:Периметр равнобедренного треугольника равен 35 см, а его основание больше боковой стороны в 1,5 разаСкачать

Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?

Геометрия | 5 — 9 классы

Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности.

Найдём высоту равнобедренного треугольника, она является медианой, поэтому делит основание пополам 36 : 2 = 18.

Пифагора h = корень из30 ^ 2 — 18 ^ 2 = корень из576 = 24, найдём площадь этого треугольника S = 1 / 2 * 36 * 24 = 432см ^ 2, эту же площадь можно вычислить через радиус описанной окружности S = abc : (4R) отсюда R = abc : (4S) = 30 * 30 * 36 : (4 * 432) = 18.

75 эту же площадь можно вычислить через радиус вписанной окружности S = 1 / 2Pr поэтому

r = 2S : P = 2 * 432 : (30 + 30 + 36) = 9

ответ 9см и 18, 75см.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.

Найти радиус вписанной и описанной окружности.

Видео:Второй признак равенства треугольников. 7 класс.Скачать

Основание равнобедренного треугольника равно16см, боковая сторона17см?

Основание равнобедренного треугольника равно16см, боковая сторона17см.

Найти радиус вписанной и описанной окружности.

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см?

В равнобедренном треугольнике основание 16 см, а боковое ребро 10 см.

Найти радиус вписанной и описанной окружности.

Видео:Найдите площадь треугольника на рисунке, если площадь четырёхугольника равна 36 ★ Как решать?Скачать

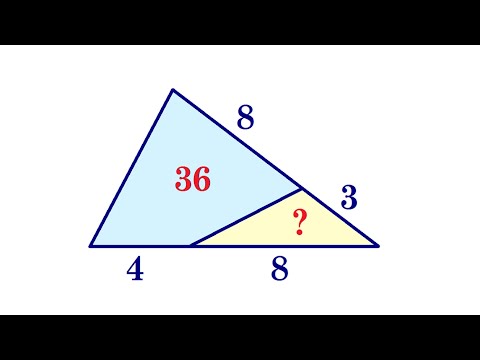
В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности?

В равнобедренном треугольнике с основанием 24 и боковой стороной 15 найти произведение радиусов описанной и вписанной окружности.

Видео:№ 107 - Геометрия 7-9 класс АтанасянСкачать

Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности?

Основание равнобедренного треугольника равно 16см, а боковые стороны 17см, найти радиус вписанной окружности.

Видео:№ 109 - Геометрия 7-9 класс АтанасянСкачать

Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см?

Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см.

Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.

Видео:36 ГРАДУСОВ + ЛЮБОВЬ СОФЬИ КОВАЛЕВСКОЙ!Скачать

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.

Найти радиус вписанной и описанной окружности.

Основание равнобедренного треугольника равно 18 см?

Основание равнобедренного треугольника равно 18 см.

Боковая сторона равна 15 см.

Найти радиусы вписанной треугольник и описанной около треугольника окружности.

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см?

Основание равнобедренного треугольника 18 см, а боковая сторона 15 см.

Найти радиус вписанной и радиус описанной окружности.

Угол при основании равнобедренного треугольника равен a?

Угол при основании равнобедренного треугольника равен a.

Радиус вписанной окружности равен r.

Найти стороны треугольника и радиус описанной окружности.

Вопрос Основание равнобедренного треугольника 36 см боковая сторона 30 см найти радиусы вписанной и описанной окружности?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Противоположные стороны прямоугольника равны. Периметр прямоугольника находят по формуле Р = 2(а + b), где a и b — стороны прямоугольника, Р — его периметр. Пусть меньшая сторона прямоугольника х см, тогда большая сторона прямоугольника равна (2х) ..

Ответ 28, 28 Сторону берем за Х. И по теореме пифагора находим эту сторону. Так как у на сквадрат то получаем Х ^ 2 + X ^ 2 = 10 ^ 2. 2X ^ 2 = 100. X ^ 2 = 50. Х = корню из 50. Х = 5 корней из 2. Ну а дальше все просто.

Окружность, вписанная в равнобедренный треугольник $ABC$, касается боковой сторон…

Окружность, вписанная в равнобедренный треугольник $ABC$, касается боковой стороны в точке $K$ (см. рис.). Найдите длину отрезка $CK$, если известно, что периметр треугольника равен $36$ и основание $AB$ равно 10.

Объект авторского права ООО «Легион»

Вместе с этой задачей также решают:

Два угла треугольника равны $48^°$ и $64^°$ (см. рис.). Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.

В параллелограмме $ABCD$ $AB = 6, AD = 9, sinA = / $. Найдите большую высоту параллелограмма.

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^°$. Боковая сторона треугольника равна $12$. Найдите площадь этого треугольника.

В параллелограмме $ABCD$ $AB = 12, AD = 16, sinA = / $. Найдите меньшую высоту параллелограмма.

Решение №655 Основание AC равнобедренного треугольника ABC равно 12.

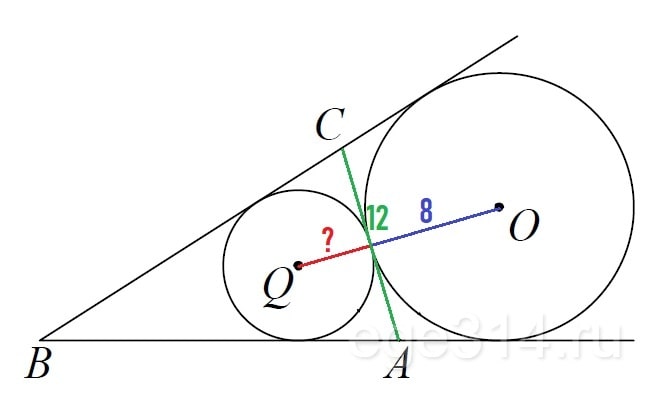
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.

О – центр не вписанной окружности, Q – центр вписанной окружности, по условию получаем рисунок:

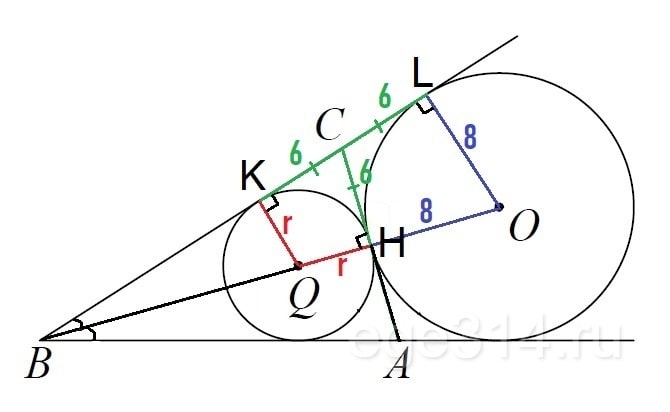
Достроим ОВ, которая является биссектрисой равнобедренного ΔАВС, а значит и медианой ⇒ CH = AH = 12/2 = 6. Достроим радиусы QK и OL к касательной DC. Радиус и касательная всегда пересекаются под прямым углом.

По свойству отрезков касательных к окружности проведённых из одной точки CH = CK = CL = 6.
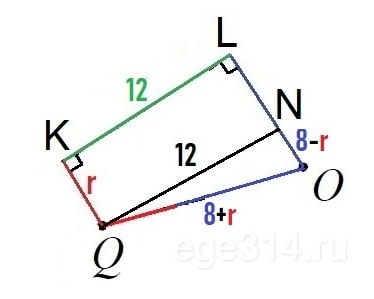
Обозначим радиус вписанной окружности – r. LOQK – прямоугольная трапеция, проведём в ней высоту и рассмотрим ΔNQO.

Сторона ON = KL = 12, как противоположные стороны прямоугольника. OQ = 8 + r, это сумма радиусов. NO = 8 – r. Треугольник прямоугольный, через теорему Пифагора найдём r:

QN 2 + ON 2 = OQ 2
12 2 + (8 – r) 2 = (8 + r) 2
144 + 64 – 16r + r 2 = 64 + 16r +r 2
– 16r + r 2 – 16r – r 2 = 64 – 144 – 64
– 32r = – 144
r = – 144/( – 32) = 4,5