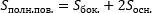- Призма
- Формулы вычисления объема и площади поверхности призмы:
- В основании лежит треугольник.
- В основании лежит четырехугольник
- 1. Прямоугольник
- 2. Ромб
- 3. Трапеция
- Рассмотрим площади правильных многоугольников:
- Подобие треугольников
- Прямоугольный треугольник и его свойства:
- Теорема Пифагора
- Теорема синусов
- Теорема косинусов
- Основание призмы прямоугольный треугольник
- Треугольная призма все формулы и примеры задач
- Определение
- Элементы треугольной призмы
- Виды треугольных призм
- Прямая треугольная призма
- Наклонная треугольная призма
- Основные формулы для расчета треугольной призмы
- Объем треугольной призмы
- Площадь боковой поверхности призмы
- Площадь полной поверхности призмы
- Пример призмы
- Задачи на расчет треугольной призмы
- 🌟 Видео
Видео:№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Призма
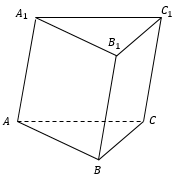
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$P_$ — периметр основания;
$S_$ — площадь основания;
$S_$ — площадь боковой поверхности;
$S_$ — площадь полной поверхности;
$h$ — высота призмы.
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/$, где $h_a$ — высота, проведенная к стороне $а$
- $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√
$, где $р$ — это полупериметр $p=/$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S=/$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
1. Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб
$S=/$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция
$S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S=/$, где $а$ — длина стороны.
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
Цилиндр — это та же призма, в основании которой лежит круг.
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $/$ | $/$ | $/$ |
| $cosα$ | $/$ | $/$ | $/$ |
| $tgα$ | $/$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $/$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Видео:№234. Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузыСкачать

Основание призмы прямоугольный треугольник
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 13 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 7 и 24, высота призмы равна 15. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4, высота призмы равна 8. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 12, высота призмы равна 14. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 8. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4, высота призмы равна 7. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 12, высота призмы равна 13. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 12, высота призмы равна 8. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 14. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 5. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 15. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 12, высота призмы равна 12. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Полная площадь поверхности:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 15 и 20, высота призмы равна 21. Найдите площадь ее поверхности.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Третья сторона треугольника в основании равна 10 и его площадь Площадь боковой поверхности призмы с периметром основания P равна
Видео:№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

Треугольная призма все формулы и примеры задач
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Видео:Геометрия Основание прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12Скачать

Определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
Видео:🔴 В основании прямой призмы лежит ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Элементы треугольной призмы
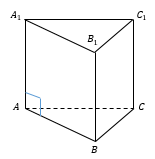
Треугольники ABC и A1B1C1 являются основаниями призмы .
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы .
Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.
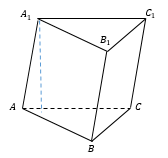
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
Видео:№235. Основанием прямой призмы является прямоугольный треугольник с острым углом φ. ЧерезСкачать
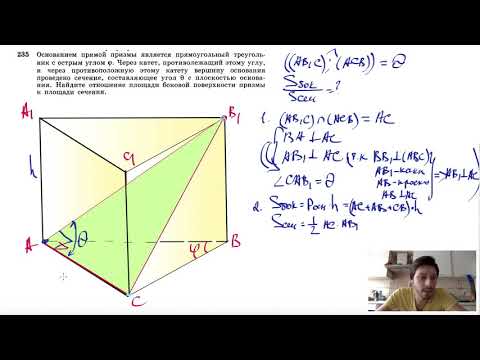
Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
Прямая треугольная призма
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Видео:🔴 В основании прямой призмы лежит прямоугольный ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
так как Sбок=Pосн . h, то получим:
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы :
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см 2 , то высота должна быть выражена в сантиметрах, а объем — в см 3 . Если площадь основания в мм 2 , то высота должна быть выражена в мм, а объем в мм 3 и т. д.
Видео:Геометрия Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 смСкачать

Пример призмы
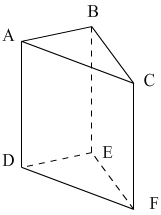
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Видео:№251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать

Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
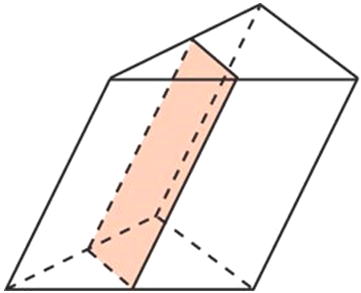
Задача 2.
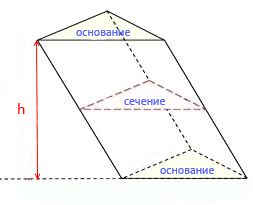
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k 2 = S12 2 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
🌟 Видео
В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые ребра призмы...Скачать

Основанием прямой треугольной призмы служит прямоугольный треугольник 8 ЗАДАНИЕ ЕГЭ МАТЕМАТИКА ПРОФИСкачать

Геометрия Основанием прямой призмы ABCA1B1C1 является прямоугольный треугольник ABC, угол C = 90Скачать

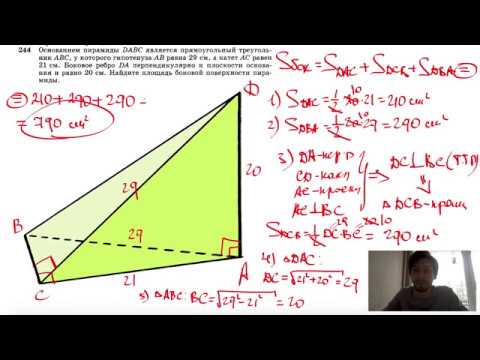
№244. Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенузаСкачать
Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Геометрия Основание прямой призмы служит прямоугольный треугольник с острым углом 15. НаибольшаяСкачать

Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Найдите объем треугольной призмыСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Г: Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 40 боковоеСкачать

Геометрия В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребраСкачать