Осевое сечение конуса правильный треугольник

Условие

Осевое сечение конуса- правильный треугольник. В конус вписана сфера. Найти ее площадь, если образующая равна 3 см

Решение

В конус вписана сфера — значит в осевое сечение вписана окружность, осевое сечение конуса– правильный треугольник

Планиметрическая задача. Найти радиус окружности , вписанной в правильный треугольник.

r=a/(2sqrt(3))=a*sqrt(3)/6=3sqrt(3)/6=sqrt(3)/2 ( cм. скрин 2)

S_(сферы)=4π*r^2=4*π(sqrt(3)/2)^2=[b]3π[/b]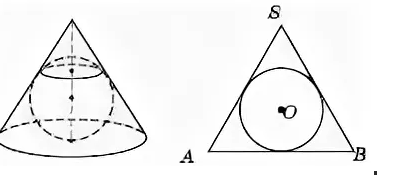

Видео:№550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, еслиСкачать

Осевое сечение конуса — правильный треугольник, длина стороны которого равна 8 см. Через две образующие, угол между которыми 30°, проведено сечение. Вычислите

Видео:№551. Осевое сечение конуса — правильный треугольник со стороной 2г. Найдите площадь сечения,Скачать

Ваш ответ

Видео:Конус. 11 класс.Скачать

решение вопроса

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Похожие вопросы

• Все категории
• экономические 43,283
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,073
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:сечение конусаСкачать

Что такое сечение конуса? Как найти площадь осевого сечения конуса

Одной из фигур, которая встречается при решении геометрических задач в пространстве, является конус. Он, в отличие от многогранников, относится к классу фигур вращения. Рассмотрим в статье, что понимают под ним в геометрии, и исследуем характеристики различных сечений конуса.

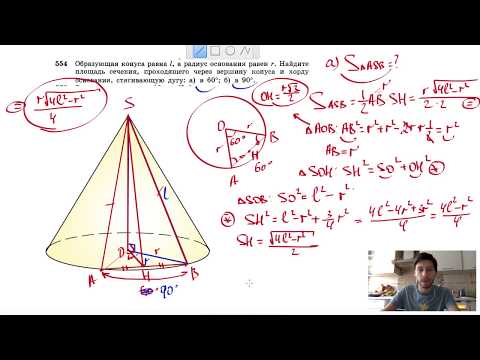
Видео:№554. Образующая конуса равна l, а радиус основания равен r. Найдите площадь сечения, проходящегоСкачать

Конус в геометрии

Предположим, что имеется некоторая кривая на плоскости. Это может быть парабола, окружность, эллипс и так далее. Возьмем точку, которая указанной плоскости не принадлежит, и соединим с ней все точки кривой. Образованная поверхность называется конической или просто конусом.

Вам будет интересно: Что такое конус: определение. Основание, вершина, высота конуса

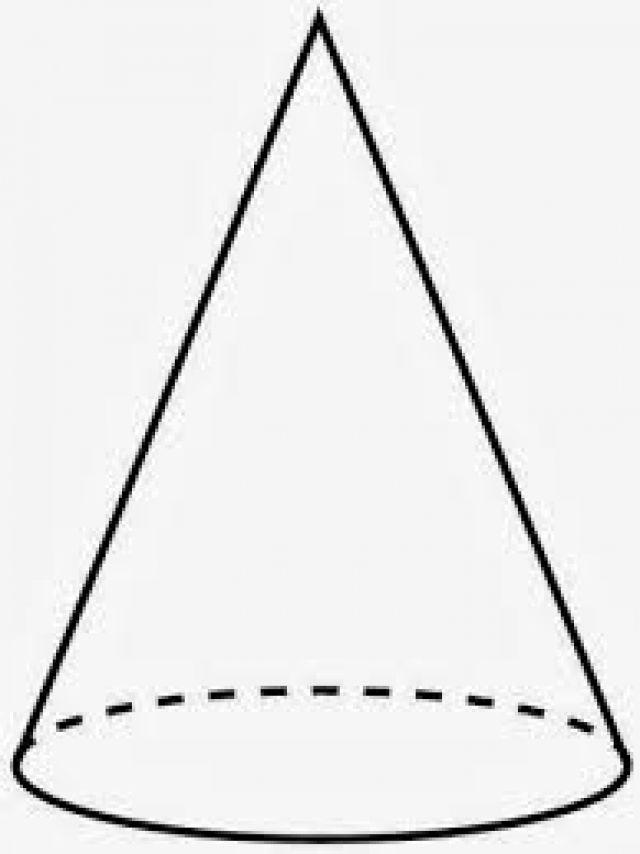
Если исходная кривая является замкнутой, тогда коническую поверхность можно заполнить веществом. Полученная таким образом фигура является объемным телом. Она также называется конусом. Несколько конусов, изготовленных из бумаги, показаны ниже на рисунке.

Коническая поверхность встречается в обычной жизни. Например, этой формой обладает мороженое-рожок или дорожный полосатый конус, который призван привлечь внимание водителей и пешеходов.

Видео:Решение задач на конусСкачать

Виды конусов

Вам будет интересно: Подберем рифму к слову «капля»

Как можно догадаться, рассматриваемые фигуры друг от друга отличаются типом кривой, на которой они образованы. Например, существует круглый конус или эллиптический. Данная кривая называется основанием фигуры. Однако форма основания — это не единственная особенность, позволяющая классифицировать конусы.

Второй важной их характеристикой является положение высоты относительно основания. Высотой конуса называется прямой отрезок, который опущен из вершины фигуры к плоскости основания и перпендикулярен этой плоскости. Если высота пересекает в геометрическом центре основание (например, в центре круга), то конус будет прямым, если перпендикулярный отрезок падает в любую другую точку основания или за его пределы, то фигура будет наклонной.

Далее в статье будем рассматривать только круглый прямой конус как яркий представитель рассматриваемого класса фигур.

Видео:Геометрия Осевым сечением конуса является прямоугольный треугольник с гипотенузой равной аСкачать

Геометрические названия элементов конуса

Выше было сказано, что конус имеет основание. Оно ограничено окружностью, которая называется направляющей конуса. Отрезки, соединяющие направляющую с точкой, не лежащей в плоскости основания, называются образующими. Совокупность всех точек образующих называется конической или боковой поверхностью фигуры. Для круглого прямого конуса все образующие имеют одинаковую длину.

Вам будет интересно: Абашевская культура бронзового века: локализация, археологические находки

Точка, где образующие пересекаются, называется вершиной фигуры. В отличие от многогранников, конус имеет единственную вершину и не имеет ни одной грани.

Прямая линия, проходящая через вершину фигуры и центр круга, называется осью. Ось содержит в себе высоту прямого конуса, поэтому она с плоскостью основания образует прямой угол. Эта информация важна при вычислении площади осевого сечения конуса.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Круглый прямой конус — фигура вращения

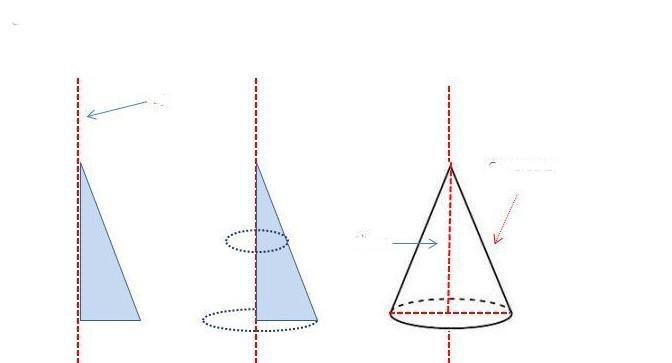
Рассматриваемый конус является достаточно симметричной фигурой, которую можно получить в результате вращения треугольника. Предположим, что имеется треугольник с прямым углом. Чтобы получить конус, достаточно вращать этот треугольник вокруг одного из катетов так, как показано на рисунке ниже.

Видно, что ось вращения является осью конуса. Один из катетов будет равен высоте фигуры, а второй катет станет радиусом основания. Гипотенуза треугольника в результате вращения опишет коническую поверхность. Она будет образующей конуса.

Указанный способ получения круглого прямого конуса удобно использовать для изучения математической связи между линейными параметрами фигуры: высоты h, радиуса круглого основания r и направляющей g. Соответствующая формула следует из свойств прямоугольного треугольника. Она приведена ниже:

Поскольку мы имеем одно уравнение и три переменных, то это означает, что для однозначного задания параметров круглого конуса необходимо знать две любые величины.

Видео:Усеченный конус. 11 класс.Скачать

Сечения конуса плоскостью, которая не содержит вершину фигуры

Вопрос построения сечений фигуры не является тривиальным. Дело в том, что форма сечения конуса поверхностью зависит от взаимного расположения фигуры и секущей.

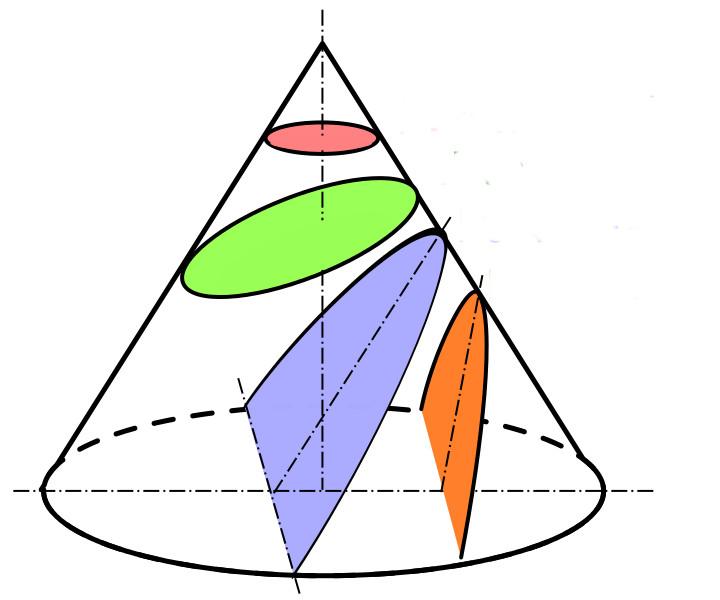
Предположим, что мы пересекаем конус плоскостью. Какое сечение получится в результате этой геометрической операции? Варианты формы сечения показаны на рисунке ниже.

Розовое сечение является кругом. Оно образовано в результате пересечения фигуры плоскостью, которая параллельна основанию конуса. Это сечения перпендикулярно оси фигуры. Образованная выше секущей плоскости фигура представляет собой конус, подобный исходному, но имеющий круг меньшего размера в основании.

Зеленое сечение — это эллипс. Он получается, если секущая плоскость не параллельна основанию, однако она пересекает только боковую поверхность конуса. Отсеченная выше плоскости фигура называется эллиптическим наклонным конусом.

Синее и оранжевое сечения имеют форму параболы и гиперболы, соответственно. Как видно из рисунка, они получаются, если секущая плоскость одновременно пересекает боковую поверхность и основание фигуры.

Для определения площадей сечений конуса, которые были рассмотрены, необходимо использовать формулы для соответствующей фигуры на плоскости. Например, для круга это умноженное на квадрат радиуса число Пи, а для эллипса — это произведение Пи на длину малой и большой полуосей:

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Сечения, содержащие вершину конуса

Теперь рассмотрим варианты сечений, которые возникают, если секущая плоскость будет проходить через вершину конуса. Возможны три случая:

Осевое сечение. Оно образуется, когда плоскость содержит не только вершину фигуры, но и всю ее ось. При этом плоскость будет перпендикулярна круглому основанию и разделит конус на две равные части.

Очевидно, что площади первых двух видов сечений равны нулю. Что касается площади сечения конуса для 3-го вида, то этот вопрос подробнее рассматривается в следующем пункте.

Видео:Тела вращения (задание 5). Что нужно знать для ЕГЭ? | Математика ЕГЭ 2022 | УмскулСкачать

Осевое сечение

Выше отмечалось, что осевым сечением конуса называется фигура, образованная при пересечении конуса плоскостью, проходящей через его ось. Несложно догадаться, что это сечение будет представлять фигуру, показанную на рисунке ниже.

Это равнобедренный треугольник. Вершина осевого сечения конуса — это вершина этого треугольника, образованная пересечением одинаковых сторон. Последние равны длине образующей конуса. Основание треугольника — это диаметр основания конуса.

Вычисление площади осевого сечения конуса сводится к нахождению площади полученного треугольника. Если изначально известны радиус основания r и высота h конуса, тогда площадь S рассматриваемого сечения будет равна:

Это выражение является следствием применения стандартной формулы для площади треугольника (половина произведения высоты на основание).

Отметим, что если образующая конуса будет равна диаметру его круглого основания, то осевое сечение конуса — треугольник равносторонний.

Треугольное сечение образуется тогда, когда секущая плоскость перпендикулярна основанию конуса и проходит через его ось. Любая другая плоскость, параллельная названной, даст в сечении гиперболу. Однако если плоскость содержит вершину конуса и пересекает его основание не через диаметр, то полученное сечение тоже будет равнобедренным треугольником.

Видео:Геометрия 11 класс (Урок№7 - Конус.)Скачать

Задача на определение линейных параметров конуса

Покажем, как пользоваться записанной для площади осевого сечения формулой для решения геометрической задачи.

Известно, что площадь осевого сечения конуса равна 100 см2. Полученный в сечение треугольник является равносторонним. Чему равны высота конуса и радиус его основания?

Поскольку треугольник равносторонний, то его высота h связана с длиной стороны a следующим соотношением:

Учитывая, что сторона треугольника в два раза больше радиуса основания конуса, и подставляя это выражение в формулу для площади сечения, получаем:

Тогда высота конуса равна:

Остается подставить значение площади из условия задачи и получить ответ:

r = √(100/√3) ≈ 7,60 см;

h = √(√3*100) ≈ 13,16 см.

Видео:№557. Две секущие плоскости перпендикулярны к оси конуса. Докажите, что площади сечений конусаСкачать

В каких областях важно знать параметры рассмотренных сечений?

Изучение различных типов сечений конуса представляет не только теоретический интерес, но также имеет практическое приложение.

Во-первых, следует отметить область аэродинамики, где с помощью конических сечений удается создавать идеальные гладкие формы твердых тел.

Во-вторых, конические сечения являются траекториями, по которым движутся космические объекты в гравитационных полях. Какой конкретно вид сечения представляет траектория движения космических тел системы, определяется соотношением их масс, абсолютных скоростей и расстояний между ними.

💡 Видео

№560. Найдите угол при вершине осевого сечения конуса, если разверткой его боковойСкачать

Сечение конусаСкачать

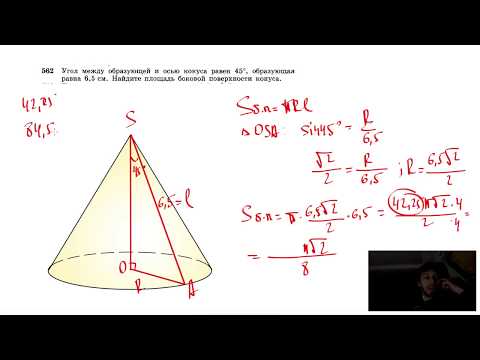
№562. Угол между образующей и осью конуса равен 45°, образующая равна 6,5 см. НайдитеСкачать

2 6 1 сечение конуса плоскостьюСкачать

№555. Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конусаСкачать