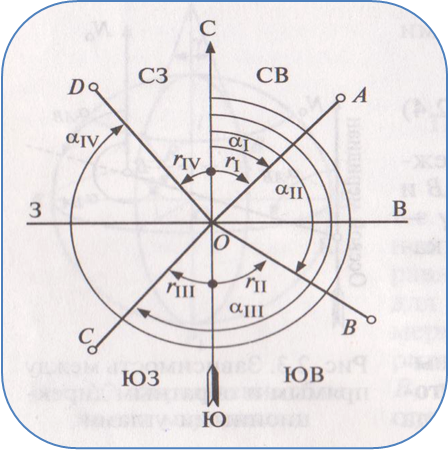
Положение линий относительно исходных направлений определяются ориентирующими углами.
Ориентирующими углами на местности служат горизонтальные углы: азимуты, дирекционные углы и румбы.
Азимутом А называется угол, отсчитываемый по ходу часовой стрелки от северного направления меридиана до данной линии. Изменяется в пределах от 0 ᵒ до 360 ◦ .
В зависимости от начала отсчёта, азимуты бывают истинными и магнитными.
Истинным азимутом Аи называется угол, отсчитываемый по ходу часовой стрелки от северного направления истинного меридиана до данной линии.
Магнитным азимутом Ам называется угол, отсчитываемый по ходу часовой стрелки от северного направления магнитного меридиана до данной линии.
Дирекционным углом α называется угол, отсчитываемый по ходу часовой стрелки от северного направления осевого меридиана зоны до данной линии.
Все углы изменяются в пределах от 0 ◦ до 360 ᵒ (рис.18).
Рис. 18 Азимуты и дирекционные углы
В отличие от азимутов дирекционные углы прямой линии постоянны на всём её протяжении, что делает применение этих углов удобными. Введение понятия дирекционного угла позволяет связать ориентирующие углы на поверхности Земли с ориентирующими углами на плоскости в проекции Гаусса – Крюгера. Из рисунков 17,18 можно записа
Аи = α + γ;
Аи = Ам + δ; отсюда
α + γ = Ам + δ;
α = Ам + δ – γ
Величина склонения магнитной стрелки в различных точках земной поверхности неодинакова. Наличие склонения магнитной стрелки обусловливается несовпадением магнитных полюсов Земли с географическими, а также наличием местных магнитных аномалий..Величина склонения меняется во времени. Поэтому ориентирование линий по магнитному меридиану выполняется с малой точностью и допускается при съёмках небольших площадей. При составлении карт ориентирование выполняют по истинному меридиану.
Азимуты и дирекционные углы бывают прямые и обратные (рис. 19).
Рис. 19 Прямые и обратные дирекционные углы
αВА = αАВ + 180 ᵒ ; АВА = ААВ + 180 ᵒ – γ ;
Иногда для ориентирования линий на местности вместо азимутов пользуются румбами. В зависимости от исходного направления румбы могут быть истинными, магнитными или дирекционными углами. Числовые значения румбов называют табличными углами. Все тригонометрические таблицы и таблицы приращений координат составлены для углов в пределах от 0 до 90°.
Румбом r называется острый угол между ближайшим северным или южным направлением меридиана и ориентируемой линией.
Румб изменяется в пределах от 0 ᵒ до 90 ᵒ .
Для ориентирования линий кроме числового значения румба необходимо указать четверть, в которой он находится. Зависимость между азимутами ( дирекционными углами) и румбами показана на рисунке 20 и в табл.1.
| Четверть | Дирекционный угол – α | Румб – r |
| І четв. СВ | α = r | r = α |
| ІІ четв. ЮВ | α = 180 ᵒ – r | r = 180 ᵒ – α |
| ІІІ четв. ЮЗ | α = 180 ᵒ + r | r = α – 180 ᵒ |
| ІV четв. СЗ | α = 360 ᵒ – r | r = 360 ᵒ – α |
Рис. 20 Зависимость между дирекционными углами и румбами
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Углы, связанные с окружностью
 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:Углы, вписанные в окружность. 9 класс.Скачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Вписанные углы в окружностиСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:Ориентированные углы. Олимпиадная математика. Be Student SchoolСкачать  Ориентированные углы в окружностиВ этом кратком справочнике поясняются понятия и теоремы, упоминаемые в книгах и задачах, опубликованных на нашем сайте. Справочник ни в кой мере претендует на полноту — это лишь необходимый комментарий к нашим задачам. Справочник формируется в соответствии с запросами наших читателей. Если Вас интересует, что означает данный термин, или что утверждает данная теорема, заполните форму, и мы ответим на Ваш вопрос. Знаком «*» помечены факты, относящиеся к данному понятию, знаком «-» помечены варианты формулировки определений. Статьи на букву ‘У’: Угол Углом называется фигура, которая состоит из точки — вершины угла — и двух различных лучей (полупрямых), исходящих из этой точки, — сторон угла. Говорят, что точка M лежит внутри угла AOB , если луч OM проходит между сторонами этого угла. —>* Каждый угол имеет определённую градусную меру , большую нуля. Развёрнутый угол равен 180 o . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. —>* От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 o , и только один.
вертикальный Два угла называются вертикальными , если стороны одного угла являются дополнительными полупрямыми сторон другого. —>* Вертикальные углы равны. внешний многоугольника Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный с углом многоугольника при этой вершине. —>* Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним (см. «теорему о внешнем угле треугольника»). —>* Сумма внешних углов (по одному при каждой вершине) выпуклого многоугольника равна 360 o . вписанный Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в данную окружность. Если BAC — угол, вписанный в окружность с центром O , то центральный угол BOC , не содержащий точку A , называется центральным углом, соответствующим данному вписанному углу . * Угол вписанный в окружность, равен половине соответствующего центрального угла. (См. задачу 52339.) * Вписанные углы, стороны которых проходят через точки A и B окружности, а вершины лежат по одну сторону от прямой AB , равны. между касательной и хордой Если прямая, проходящая через точку A , касается окружности в точке M , отличной от A , то углом между касательной AM и хордой MB называется угол AMB . * Градусная мера угла между касательной и хордой равна половине градусной меры дуги, заключенной внутри этого угла (теорема об угле между касательной и хордой). (См. задачу 52425.) * Если точки M и B лежат на окружности, а точка A — вне окружности и при этом градусная мера угла AMB равна половине градусной меры дуги MB , заключенной внутри этого угла, то прямая AM — касательная к данной окружности.
ориентированный Величиной ориентированного угла между прямыми AB и CD (обозначение: 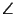 ( AB , CD )) называют величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD . При этом углы, отличающиеся на n . 180 o ( n — целое число), считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме 180 o или, что по нашему соглашению то же самое, 0 o ). ( AB , CD )) называют величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD . При этом углы, отличающиеся на n . 180 o ( n — целое число), считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме 180 o или, что по нашему соглашению то же самое, 0 o ).Ориентированные углы обладает следующими свойствами: а) б) в) точки A , B , C , D , не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда
смежный Два угла называются смежными , если одна сторона у них общая, а две другие стороны этих углов являются дополнительными полупрямыми. —>* Сумма смежных углов равна 180 o .
Проект осуществляется при поддержке и . 📺 ВидеоВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать  ОГЭ I Углы в окружности I Задание 16Скачать  Углы, вписанные в окружность. Практическая часть. 9 класс.Скачать  Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать  Вписанные и центральные углыСкачать  ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать  Центральный угол в окружностиСкачать  Вписанный угол в окружность ❤️ #геометрияСкачать  Углы, вписанные в окружность. Практическая часть. 9 класс.Скачать  Длина дуги окружности. 9 класс.Скачать  Как понять центральные и вписанные углыСкачать  8 класс, 34 урок, Теорема о вписанном углеСкачать  Углы, связанные с окружностьюСкачать  Углы, вписанные в окружность. Практическая часть. 9 класс.Скачать  |



































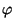 =
= 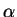 , где
, где