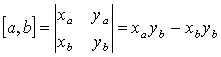Ориентированная площадь треугольника это (6 видео)

Ориентированная площадь треугольника это

Ориентированной площадью треугольника ABC называется величина (ABC), равная его площади, взятой со знаком плюс, если обход треугольника в порядке A–B–C–A совершается против часовой стрелки и со знаком минус, если по часовой стрелке (рис. 1). Таким образом, строго говоря, ориентированная площадь (ABC) определена не для треугольника как такового, а для «ориентированного треугольника», т.е. треугольника с заданным порядком вершин, причем (ABC) = (CAB) = (BCA) = –(ACB) = –(BAC) = –(CBA).

С помощью ориентированной площади во многих ситуациях можно избавиться от необходимости рассматривать разные расположения точек. Например, если точка D лежит внутри треугольника ABC (рис. 2), то справедливо равенство:

(которое, в частности, используется при выводе формулы площади треугольника через радиус вписанной окружности); если D лежит вне треугольника, но внутри угла ABC, то S_ABC = S_DAB + S_DBC – S_DCA, для других расположений получатся другие наборы знаков в левой части. Равенство для ориентированных площадей
(ABC) = (DAB) + (DBC) + (DCA) (1)
справедливо при любом расположении точек A, B, C, D на плоскости. Также имеет место векторное равенство
,
из которого следует, что барицентрические координаты точки D относительно треугольника ABC пропорциональны ориентированным площадям треугольников DBC, DCA, DAB.

Если координаты точек A и B равны (x_A;y_A) и (x_B; y_B), то ориентированная площадь треугольника OAB, где O – начало координат, равна
(OAB) =( x_A y_B – y_A x_B)
(при этом треугольник с вершинами (0; 0), (1; 0), (0; 1) считается положительно ориентированным). Эта формула позволяет написать выражение для площади произвольного треугольника ABC через координаты его вершин: для этого надо записать в координатах правую часть формулы (1), взяв в ней D = O). Приведем обобщение этой формулы для произвольного n-угольника A₁A₂. A_n:

(A₁A₂. A_n) = ((x₁y₂–y₁x₂) + (x₂y₃–y₂x₃) + . + (x_{n – 1}y_n – y_{n – 1}x_n) + (x_ny₁ – y_nx₁)), (2)

где (x_i; y_i) – координаты точки A_i. Можно показать, что модуль этой величины равен (обычной) площади n-угольника, а знак определяется направлением обхода вершин в порядке A₁ – A₂ – … – A_n – A₁, как и в случае треугольника. При этом правая часть (2) не зависит от того, с какой вершины начинать обход – существенна только последовательность вершин. Если же поменять порядок на обратный – A_nA _{n – 1}. A₁, то и знак правой части равенства (2) изменится на обратный (а модуль не изменится).

«Направление против часовой стрелки» не является математически строгим понятием, поэтому и данное в начале определение нестрогое. Формализовать наглядное представление о «направлении обхода», или «ориентации», многоугольника довольно сложно. Наиболее простой путь – непосредственно использовать формулу (2) как определение ориентированной площади; тогда многоугольник можно считать положительно или отрицательно ориентированным в зависимости от знака его ориентированной площади. Нетрудно проверить, что при этом будут выполняться интуитивно понятные утверждения об ориентации, например: два треугольника в общей стороной – ABC и ABD будут одинаково ориентированы тогда и только тогда, когда вершины C и D лежат по одну сторону от AB, при осевой симметрии ориентация многоугольника меняется на противоположную и др.

Содержание

Знаковая площадь треугольника и предикат «По часовой стрелке»
Определение
Вычисление
Реализация
Площадь многоугольника
📽️ Видео

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Знаковая площадь треугольника и предикат «По часовой стрелке»

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

Определение

Пусть даны три точки , , . Найдём значение знаковой площади треугольника , т.е. площади этого треугольника, взятой со знаком плюс или минус в зависимости от типа поворота, образуемого точками , , : против часовой стрелки или по ней соответственно.

Понятно, что, если мы научимся вычислять такую знаковую («ориентированную») площадь, то сможем и находить обычную площадь любого треугольника, а также сможем проверять, по часовой стрелке или против направлена какая-либо тройка точек.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Вычисление

Воспользуемся понятием косого (псевдоскалярного) произведения векторов. Оно как раз равно удвоенной знаковой площади треугольника:

где угол берётся ориентированным, т.е. это угол вращения между этими векторами против часовой стрелки.

(Модуль косого произведения двух векторов равен модулю векторного произведения их.)

Косое произведение вычисляется как величина определителя, составленного из координат точек:

Раскрывая определитель, можно получить такую формулу:

Можно сгруппировать третье слагаемое с первыми двумя, избавившись от одного умножения:

Последнюю формулу удобно записывать и запоминать в матричном виде, как следующий определитель:

Видео:Хаттуша. 1 часть. Параметры отверстий блоков Нижнего города. Организатор @antik_ruinsСкачать

Реализация

Функция, вычисляющая удвоенную знаковую площадь треугольника:

Функция, возвращающая обычную площадь треугольника:

Функция, проверяющая, образует ли указанная тройка точек поворот по часовой стрелке:

Функция, проверяющая, образует ли указанная тройка точек поворот против часовой стрелки:

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Площадь многоугольника

Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами AB и AC . То есть ее знак зависит от порядка перечисления вершин.

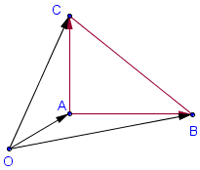
Рисунок №1

На рис. 1 треугольник АВС – прямоугольный. Его ориентированная площадь равна S=| OB || OC |/2(она больше нуля, так как пара OB , OC ориентирована положительно). Эту же величину можно вычислить другим способом.

Пусть О – произвольная точка плоскости. На рисунке площадь треугольника ABC получится, если из площади треугольника OBC вычесть площади OAB и OCA. Таким образом, нужно просто сложить ориентированные площади треугольников OAB, OBC и OCA. Это правило работает при любом выборе точки О.

Точно так же для вычисления площади любого многоугольника A₁A₂. A_n нужно сложить ориентированные площади треугольников OA₁A₂,OA₂A₃. OA_nA₁

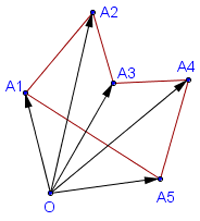
Рисунок №2

В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной A₁A₂. A_n многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).

Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Теперь необходимо выразить ее в координатах.

Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах.

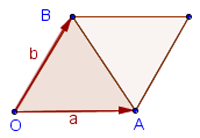
Рисунок №3

Векторное произведение, выраженное через координаты векторов:

В качестве точки О удобно взять начало координат, тогда координаты векторов, на основании которых вычисляются ориентированные площади, совпадут с координатами точек.

Пусть (х₁, y₁), (x₂, у₂), . (х_n,у_n) —координаты вершин заданного многоугольника в порядке обхода по или против часовой стрелки. Тогда его ориентированная площадь S будет равна:

Это и есть рабочая формула.

Если координаты вершин были заданы в порядке обхода против часовой стрелки, то число S, вычисленное по этой формуле, получится положительным. В противном случае оно будет отрицательным, и для получения обычной геометрической площади необходимо взять его абсолютное значение.