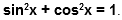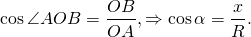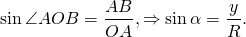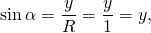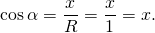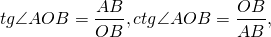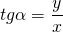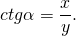Введем основные тригонометрические функции.
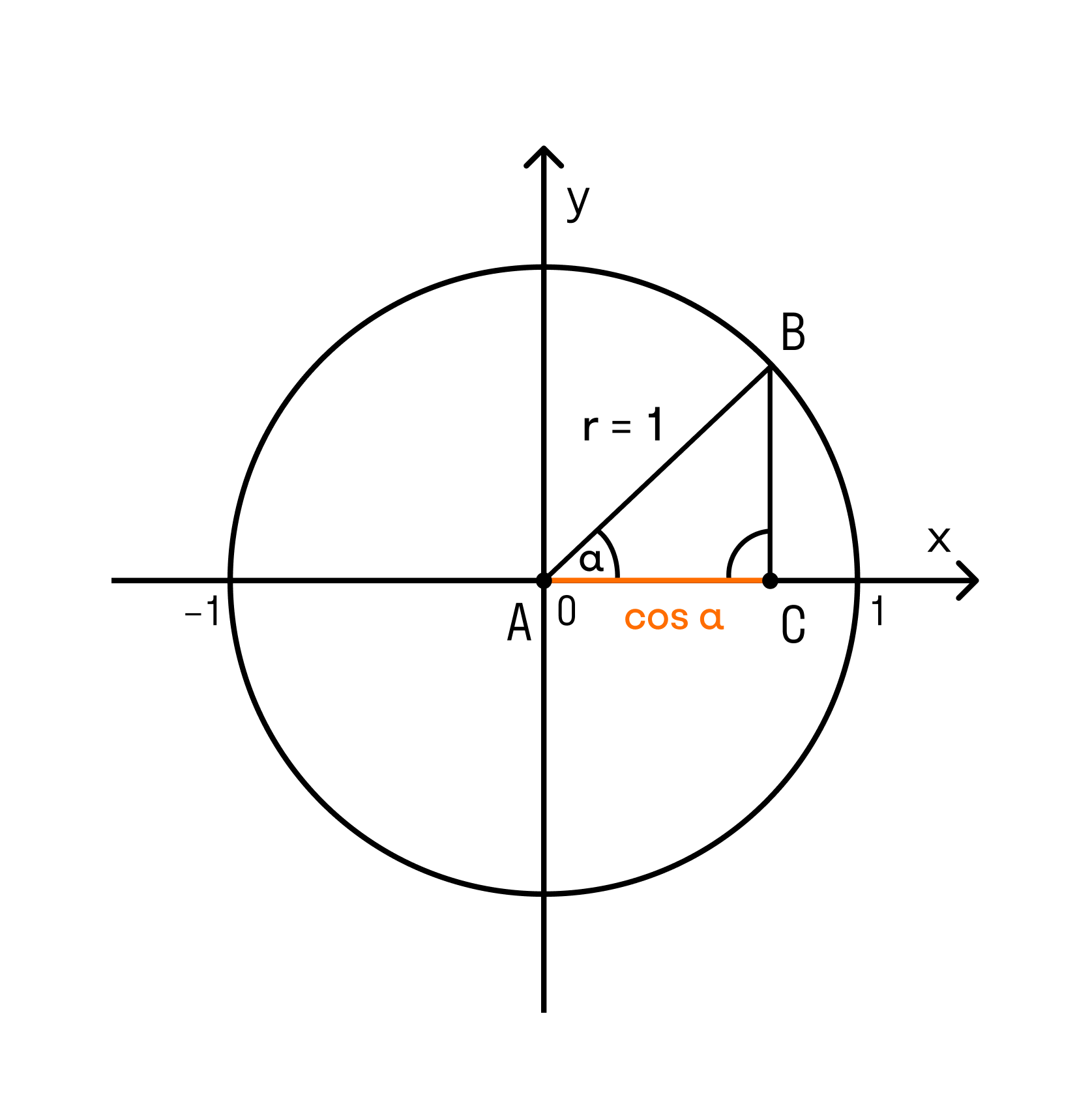
Пусть радиус-вектор $vec = bar$ точки $M$ образует угол $alpha$ с осью $Ox$ (рис.), причем $x$ и $y$ соответственно абсцисса и ордината конца $M$ вектора, $r$ — его модуль, а величина угла $alpha$ измеряется в градусах или в радианах.
1. Синусом угла $alpha$ (обозначение: $sin alpha$) называется отношение ординаты $y$ (см. рис.) к длине $r$ радиуса-вектора $bar $:
2. Косинусом угла $alpha$ (обозначение: $cos alpha$) называется отношение абсциссы $x$ к длине $r$ радиуса-вектора $bar $:
3. Тангенсом угла $alpha$ (обозначение: $tg alpha$) называется отношение синуса угла $alpha$ к косинусу этого угла:
4. Котангенсом угла $alpha$ (обозначение: $ctg alpha$) называется отношение косинуса угла $alpha$ к синусу этого угла:
5. Секансом угла $alpha$ (обозначение: $sec alpha$) называется величина, обратная $cos alpha$:
6. Косекансом угла $alpha$ (обозначение: $cosec alpha$) называется величина, обратная $sin alpha$:
Замечание 1. Тригонометрические функции (1) — (6) действительно являются функциями только угла $alpha$, т. е. не зависят от длины подвижного радиуса-вектора. Для того чтобы в этом убедиться, достаточно доказать, что если подвижный радиус-вектор $vec$ образует с осью абсцисс данный угол $alpha$, то отношения $frac$ и $frac$ не зависят от длины радиуса-вектора.
Замечание 2. Из определения $tg alpha$ и $ctg alpha$ следует, что
$tg alpha = frac$, (7)
$ctg alpha = frac$. (8)
Соотношения (7) и (8) можно было бы принять в качестве определений для $tg alpha$ и $ctg alpha$.
Замечание 3. Аналогично получаем
$sec alpha = frac$,(9)
$cosec alpha = frac$ (10).
Соотношения (9) и (10) можно было бы также принять в качестве определений для $sec alpha$ и $cosec alpha$.
Замечание 4. Во всех определениях (1) — (6) предполагаем, что соответствующие отношения существуют (имеют смысл). Например, $tg alpha$ имеет смысл, если $cos alpha neq 0, ctg alpha$ имеет смысл, если $sin alpha neq 0$, и т.д. Поскольку (замечание 1) тригонометрические функции (1) — (6) угла $alpha$ не зависят от длины подвижного радиуса-вектора, то в качестве радиуса-вектора можно брать вектор с длиной, равной единице $(| vec| = r = 1)$. Такой вектор называют единичным радиусом-вектором. В случае единичного радиуса-вектора формулы для основных тригонометрических функций запишутся так (рис.):
$begin sin alpha = y, cos alpha = x \ tg alpha = frac, ctg alpha = frac \ sec alpha = frac, cosec alpha = frac end$. (11)
Формулы для $tg alpha$ и $ctg alpha$ остались прежними (см. (7) и (8)), а формулы для остальных основных тригонометрических функций приняли более простой вид (см. (1), (2), (9) и (10)). Следовательно, синус и косинус угла а равны соответственно ординате и абсциссе конца подвижного единичного радиуса-вектора. Конец этого единичного радиуса-вектора при изменении угла а от $0^$ до $360^$ опишет окружность, называемую единичной окружностью (рис.). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов. Осью тангенсов называется перпендикуляр, восставленный в точке $A$ к неподвижному радиусу-вектору $bar$. Положительное и отрицательное направления на оси тангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси ординат (рис.). Рассмотрим угол $alpha = angle AOM$ и введем понятие соответствующей точки оси тангенсов.
а) Если точка $M$ единичной окружности лежит справа от оси ординат, то соответствующей ей точкой оси тангенсов назовем точку $M_$ (точку пересечения продолжения $MO$ с осью тангенсов, рис а.
б) Если точка $M$ единичной окружности лежит слева от оси ординат, то соответствующей ей точкой сси тангенсов назовем точку $M_$ (точку пересечения продолжения $MO$ с ссыо тангенсов, рис. б.
Заметим, что тангенс угла а численно равен ординате $y_$ (рис.) соответствующей точки сси тангенсов, т. е. всегда $tg alpha — y_$. Докажем это для углов первых двух четвертей:
1) $0^ leq alpha < 90^$ (рис. a), $tg alpha = frac<y_> = y_ geq 0$, где $y_$ — ордината точки $M_$.
2) $90^ < alpha leq 180^$ (рис. б). $tg alpha = frac<y_><x_> leq 0$, где $x_$ и $y_$ — абсцисса и ордината точки $M$. Из подобия прямоугольных треугольников $OMM_$ и $OM_A$ имеем
Следовательно, $tg alpha = frac<y_><x_> = y_ leq 0$.
Заметим еще следующее:
а) если точка $M$ лежит на оси ординат (например, $alpha = 270^$), то соответствующей ей точки сси тангенсов не существует, но при этом и $tg alpha$ также не существует;
б) в рассмотренных случаях 1)-2) мы брали угол $alpha$ в пределах от $0^$ до $360^$, но в наших рассуждениях ничего не изменится, если мы будем предполагать угол $alpha$ любым.
Осью котангенсов называется перпендикуляр, восставленный в точке В (конец радиуса-вектора $bar $, образующего с осью $Ox$ угол, равный $90^$) к оси ординат. Положительное и отрицательное направления на оси котангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси абсцисс (рис.). Введем понятие соответствующей точки оси котангенсов.
а) Если точка $M$ единичной окружности лежит над осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку $M_$ (точку пересечения продолжения $OM$ с осью котангенсов, рис. а).
б) Если точка $M$ единичной окружности лежит под осью абсцисс, то соответствующей ей точкой сси котангенсов назовем точку (точку пересечения продолжения $MO$ с осью котангенсов, рис. б).
Аналогично предыдущему можно получить, что котангенс угла $alpha$ равен абсциссе $x_$ соответствующей точки оси котангенсов, т. е. $ctg alpha = x_$. Если точка $M$ лежит на оси абсцисс (например, $alpha — 180^$), то соответствующей ей точки оси котангенсов не существует, но при этом и $ctg alpha$ также не существует.
Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Тригонометрические функции
Определения тригонометрическим функциям даются с помощью тригонометрической окружности, под которой понимается окружность единичного радиуса с центром в начале координат.
Рассмотрим два радиуса этой окружности: неподвижный (где точка ) и подвижный (где точка ). Пусть подвижный радиус образует с неподвижным угол .
Число, равное ординате конца единичного радиуса, образующего угол с неподвижным радиусом , называется синусом угла : .
Число, равное абсциссе конца единичного радиуса, образующего угол с неподвижным радиусом , называется косинусом угла : .
Таким образом, точка , являющаяся концом подвижного радиуса, образующего угол , имеет координаты .
Тангенсом угла называется отношение синуса этого угла к его косинусу: , , .
Котангенсом угла называется отношение косинуса этого угла к его синусу: , , .
Геометрический смысл тригонометрических функций
Геометрический смысл синуса и косинуса на тригонометрической окружности понятен из определения: это абсцисса и ординат точки пересечения подвижного радиуса, составляющего угол с неподвижным радиусом, и тригонометрической окружности. То есть , .
Рассмотрим теперь геометрический смысл тангенса и котангенса. Треугольники подобен по трем углам (, ), тогда имеет место отношение . С другой стороны, в , следовательно .


Также подобен по трем углам (, ), тогда имеет место отношение . С другой стороны, в , следовательно .
С учетом геометрического смысла тангенса и котангенса вводят понятие оси тангенсов и оси котангенсов.
Осями тангенсов называются оси, одна из которых касается тригонометрической окружности в точке и направлена вверх, вторая касается окружности в точке и направлена вниз.
Осями котангенсов называются оси, одна из которых касается тригонометрической окружности в точке и направлена вправо, вторая касается окружности в точке и направлена влево.
Свойства тригонометрических функций
Рассмотрим некоторые основные свойства тригонометрических функций. Остальные свойства будут рассмотрены в разделе, посвященном графикам тригонометрических функций.
Область определения и область значений
Как уже было сказано ранее, синус и косинус существуют для любых углов, т.е. областью определения этих функций является множество действительных чисел. По определению тангенс не существует для углов , , а котангенс для углов , .
Поскольку синус и косинус являются ординатой и абсциссой точки на тригонометрической окружности, их значения лежат в промежутке . Областью значения тангенса и котангенса является множество действительных чисел (в этом нетрудно убедиться, глядя на оси тангенсов и котангенсов).
Рассмотрим тригонометрические функции двух углов (который соответствует подвижному радиусу ) и (который соответствует подвижному радиусу ). Поскольку , значит точка имеет координаты . Поэтому , т.е. синус — функция нечетная; , т.е. косинус — функция четная; , т.е. тангенс нечетен; , т.е. котангенс также нечетен.
Знаки тригонометрических функций для различных координатных четвертей следуют из определения этих функций. Следует отметить, что поскольку тангенс и котангенс являются отношениями синуса и косинуса, они положительны, когда синус и косинус угла имеют одинаковые знаки и отрицательны когда разные.
Периодичность синуса и косинуса основана на том факте, что углы, отличающиеся на целое количество полных оборотов, соответствуют одному и тому же взаимному расположению подвижного и неподвижного лучей. Соответственно и координаты точки пересечения подвижного луча и тригонометрической окружности будут одинаковы для углов, отличающихся на целое количество полных оборотов. Таким образом, периодом синуса и косинуса является и , , где .
Очевидно, что также является периодом для тангенса и котангенса. Но существует ли меньший период для этих функций? Докажем, что наименьшим периодом для тангенса и котангенса является .



Рассмотрим два угла и . Оп геометрическому смыслу тангенса и котангенса , , , . По стороне и прилежащим к ней углам равны треугольники и , значит равны и их стороны, значит и . Аналогичным образом можно доказать, то , , где . Таким образом, периодом тангенса и котангенса является .
Тригонометрические функции основных углов
Для успешного решения тригонометрических задач необходимо владеть многочисленными тригонометрическими формулами. Тем не менее, нет необходимости заучивать все формулы. Знать наизусть нужно лишь самые основные, а остальные формулы нужно уметь при необходимости вывести.
Основное тригонометрическое тождество и следствия из него
Все тригонометрические функции произвольного угла связаны между собой, т.е. зная одну функции всегда можно найти остальные. Эту связь дают формулы, рассматриваемые в данном разделе.
Теорема 1 (Основное тригонометрическое тождество). Для любого справедливо тождество
Доказательство состоит в применении теоремы Пифагора для прямоугольного треугольника с катетами , и гипотенузой .
Справедлива и более общая теорема.
Теорема 2. Для того, чтобы два числа можно было принять за косинус и синус одного и того же вещественного угла , необходимо и достаточно, чтобы сумма их квадратов была равна единице:
Рассмотрим следствия из основного тригонометрического тождества.
Выразим синус через косинус и косинус через синус:
В данный формулах знак плюс или минус перед корнем выбирается в зависимости от четверти, в которой лежит угол.
Подставляя полученные выше формулы в формулы, определяющие тангенс и котангенс, получаем:
Разделив основное тригонометрическое тождество почленно на или получим соотвественно:
Эти соотношения можно переписать в виде:

Следующие формулы дают связь между тангенсом и котангенсом. Поскольку при , а при , то имеет место равенство:

Формулы приведения
С помощью формул приведения можно выразить значения тригонометрических функций произвольных углов через значения функций острого угла. Все формулы приведения могут быть обобщены с помощью следующего правила.
Любая тригонометрическая функция угла , по абсолютной величине равна той же функции угла , если число — четное, и ко-функции угла , если число — нечетное. При этом если функция угла , положительна, когда — острый положительный угол, то знаки обеих функций одинаковы, если отрицательна, то различны.
Формулы суммы и разность углов
Теорема 3. Для любых вещественных и справедливы следующие формулы:
Доказательство остальных формул основано на формулах приведения и четности/нечетности тригонометрических функций.

Что и требовалось доказать.
Теорема 4. Для любых вещественных и , таких, что
1. , , , , справедливы следующие формулы
2. , , , , справедливы следующие формулы


Доказательство. По определению тангенса
Последнее преобразование получено делением числителя и знаменателя этой дроби на .
Аналогично для котангенса (числитель и знаменатель в этом случае делятся на ):
Что и требовалось доказать.
Следует обратить внимание на тот факт, что правые и левые части последних равенств имеют разные области допустимых значений. Поэтому применение этих формул без ограничений на возможные значения углов может привести к неверным результатам.
Формулы двойного и половинного угла
Формулы двойного угла позволяют выразить тригонометрические функции произвольного угла через функции угла в два раза меньше исходного. Эти формулы являются следствиями формул суммы двух углов, если положить в них углы равными друг другу.
Последнюю формулу можно преобразовать с помощью основного тригонометрического тождества:
Таким образом, для косинуса двойного угла существует три формулы:
Следует отметить, что данная формула справедлива только при
Последняя формула справедлива при , .
Аналогично функциям двойного угла могут быть получены функции тройного угла. Здесь данные формулы приводятся без доказательства:
Формулы половинного угла являются следствиями формул двойного угла и позволяют выразить тригонометрические функции некоторого угла через функции угла в два раза больше исходного.
Произведем следующие преобразования:
и выразим через :
Аналогичные преобразования произведем для :
Последние две формулы носят названия формул понижения степени.
Выведем формулу для :
Универсальная тригонометрическая подстановка
Эта группа формул позволяет выражать значения всех тригонометрических функций через тангенс половинного угла. Данные формулы часто используются при решении уравнений и произведении преобразований.
Для того, чтобы выразить через воспользуемся ранее выведенной формулой:

Далее используя формулу и только что выведенное соотношение для косинуса получим зависимость между и :
последняя формула также имеет смысл при , .
Формулы для тангенса и котангенса получаются при помощи формул двойного угла:
Формулы произведения тригонометрических функций
Данная группа формул является следствием формул суммы и разности двух углов.
Теорема 5. Для любых вещественных и справедливы следующие соотношения:
Доказательство. Запишем формулы косинуса и синуса суммы и разности для углов и :

Произведем следующие преобразования:
Что и требовалось доказать.
Формулы суммы и разности тригонометрических функций
Эти формулы также являются следствием формул суммы и разности двух углов.
Для получения формул суммы и разности функций заметим, что любые углы и можно представить следующим образом:
Найдем сумму синусов двух произвольных углов и :
Найдем разность синусов двух произвольных углов и :
Найдем сумму косинусов двух произвольных углов и :
Найдем разность косинусов двух произвольных углов и :
Найдем сумму и разность тангенсов двух углов и , таких что
Найдем сумму и разность котангенсов двух углов и , таких что , , :
Видео:Алгебра 10 класс (Урок№30 - Определение синуса, косинуса и тангенса угла.)Скачать

Ордината точки лежащая на единичной окружности
Видео:Определение синуса косинуса тангенса котангенса на единичной окружности. Шпаргалка по тригонометрииСкачать

Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Алгебра 10 класс (Урок№29 - Радианная мера угла.)Скачать

Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Определение синуса и косинуса на единичной окружности | Алгебра 10 класс #11 | ИнфоурокСкачать

Ордината точки лежащая на единичной окружности
Введем основные тригонометрические функции.
Пусть радиус-вектор $vec = bar $ точки $M$ образует угол $alpha$ с осью $Ox$ (рис.), причем $x$ и $y$ соответственно абсцисса и ордината конца $M$ вектора, $r$ — его модуль, а величина угла $alpha$ измеряется в градусах или в радианах.
1. Синусом угла $alpha$ (обозначение: $sin alpha$) называется отношение ординаты $y$ (см. рис.) к длине $r$ радиуса-вектора $bar $:
2. Косинусом угла $alpha$ (обозначение: $cos alpha$) называется отношение абсциссы $x$ к длине $r$ радиуса-вектора $bar $:
3. Тангенсом угла $alpha$ (обозначение: $tg alpha$) называется отношение синуса угла $alpha$ к косинусу этого угла:
4. Котангенсом угла $alpha$ (обозначение: $ctg alpha$) называется отношение косинуса угла $alpha$ к синусу этого угла:
5. Секансом угла $alpha$ (обозначение: $sec alpha$) называется величина, обратная $cos alpha$:
6. Косекансом угла $alpha$ (обозначение: $cosec alpha$) называется величина, обратная $sin alpha$:
Замечание 1. Тригонометрические функции (1) — (6) действительно являются функциями только угла $alpha$, т. е. не зависят от длины подвижного радиуса-вектора. Для того чтобы в этом убедиться, достаточно доказать, что если подвижный радиус-вектор $vec $ образует с осью абсцисс данный угол $alpha$, то отношения $frac $ и $frac $ не зависят от длины радиуса-вектора.
Замечание 2. Из определения $tg alpha$ и $ctg alpha$ следует, что
$tg alpha = frac $, (7)
$ctg alpha = frac $. (8)
Соотношения (7) и (8) можно было бы принять в качестве определений для $tg alpha$ и $ctg alpha$.
Замечание 3. Аналогично получаем
$sec alpha = frac $,(9)
$cosec alpha = frac $ (10).
Соотношения (9) и (10) можно было бы также принять в качестве определений для $sec alpha$ и $cosec alpha$.
Замечание 4. Во всех определениях (1) — (6) предполагаем, что соответствующие отношения существуют (имеют смысл). Например, $tg alpha$ имеет смысл, если $cos alpha neq 0, ctg alpha$ имеет смысл, если $sin alpha neq 0$, и т.д. Поскольку (замечание 1) тригонометрические функции (1) — (6) угла $alpha$ не зависят от длины подвижного радиуса-вектора, то в качестве радиуса-вектора можно брать вектор с длиной, равной единице $(| vec | = r = 1)$. Такой вектор называют единичным радиусом-вектором. В случае единичного радиуса-вектора формулы для основных тригонометрических функций запишутся так (рис.):
$begin sin alpha = y, cos alpha = x \ tg alpha = frac , ctg alpha = frac \ sec alpha = frac , cosec alpha = frac end $. (11)
Формулы для $tg alpha$ и $ctg alpha$ остались прежними (см. (7) и (8)), а формулы для остальных основных тригонометрических функций приняли более простой вид (см. (1), (2), (9) и (10)). Следовательно, синус и косинус угла а равны соответственно ординате и абсциссе конца подвижного единичного радиуса-вектора. Конец этого единичного радиуса-вектора при изменении угла а от $0^ $ до $360^ $ опишет окружность, называемую единичной окружностью (рис.). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов. Осью тангенсов называется перпендикуляр, восставленный в точке $A$ к неподвижному радиусу-вектору $bar $. Положительное и отрицательное направления на оси тангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси ординат (рис.). Рассмотрим угол $alpha = angle AOM$ и введем понятие соответствующей точки оси тангенсов.
а) Если точка $M$ единичной окружности лежит справа от оси ординат, то соответствующей ей точкой оси тангенсов назовем точку $M_ $ (точку пересечения продолжения $MO$ с осью тангенсов, рис а.
б) Если точка $M$ единичной окружности лежит слева от оси ординат, то соответствующей ей точкой сси тангенсов назовем точку $M_ $ (точку пересечения продолжения $MO$ с ссыо тангенсов, рис. б.
Заметим, что тангенс угла а численно равен ординате $y_ $ (рис.) соответствующей точки сси тангенсов, т. е. всегда $tg alpha — y_ $. Докажем это для углов первых двух четвертей:
1) $0^ leq alpha $ (рис. a), $tg alpha = frac > = y_ geq 0$, где $y_ $ — ордината точки $M_ $.
2) $90^ $ (рис. б). $tg alpha = frac > > leq 0$, где $x_ $ и $y_ $ — абсцисса и ордината точки $M$. Из подобия прямоугольных треугольников $OMM_ $ и $OM_ A$ имеем
Следовательно, $tg alpha = frac > > = y_ leq 0$.
Заметим еще следующее:
а) если точка $M$ лежит на оси ординат (например, $alpha = 270^ $), то соответствующей ей точки сси тангенсов не существует, но при этом и $tg alpha$ также не существует;
б) в рассмотренных случаях 1)-2) мы брали угол $alpha$ в пределах от $0^ $ до $360^ $, но в наших рассуждениях ничего не изменится, если мы будем предполагать угол $alpha$ любым.
Осью котангенсов называется перпендикуляр, восставленный в точке В (конец радиуса-вектора $bar $, образующего с осью $Ox$ угол, равный $90^ $) к оси ординат. Положительное и отрицательное направления на оси котангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси абсцисс (рис.). Введем понятие соответствующей точки оси котангенсов.
а) Если точка $M$ единичной окружности лежит над осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку $M_ $ (точку пересечения продолжения $OM$ с осью котангенсов, рис. а).
б) Если точка $M$ единичной окружности лежит под осью абсцисс, то соответствующей ей точкой сси котангенсов назовем точку (точку пересечения продолжения $MO$ с осью котангенсов, рис. б).
Аналогично предыдущему можно получить, что котангенс угла $alpha$ равен абсциссе $x_ $ соответствующей точки оси котангенсов, т. е. $ctg alpha = x_ $. Если точка $M$ лежит на оси абсцисс (например, $alpha — 180^ $), то соответствующей ей точки оси котангенсов не существует, но при этом и $ctg alpha$ также не существует.
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Единичная окружность
Что такое единичная окружность и как с ее помощью вводятся определения синуса, косинуса, тангенса и котангенса?
Рассмотрим в прямоугольной декартовой системе координат окружность с центром в начале координат — точке O.
Отметим на окружности точку P, лежащую на оси абсцисс справа от точки O.
Осуществим поворот радиуса OP около точки O на угол α в верхнюю полуплоскость.
При этом радиус OP займет положение OA. Говорят, что при повороте на угол альфа радиус OP переходит в радиус OA, а точка P переходит в точку точку A(x;y).
Опустив перпендикуляр AB из точки A на ось Оx, получим прямоугольный треугольник OAB, в котором гипотенуза OA равна радиусу окружности, катеты AB и OB — ординате и абсциссе точки A: OA=R, AB=y, OB=x.
Катет AB — противолежащий углу AOB, равному α, катет OB — прилежащий.
По определению косинуса острого угла в прямоугольном треугольнике,
Таким образом, на окружности косинус угла α — это отношение абсциссы точки A окружности к радиусу этой окружности.
Аналогично, по определению синуса острого угла в прямоугольном треугольнике,
Значит, синус угла α — это отношение ординаты точки A окружности к радиусу этой окружности.
Для окружности любого радиуса отношения x/R и y/R не зависят от величины радиуса, а зависят только от угла альфа. Поэтому удобно взять R=1. Для окружности единичного радиуса определение синуса и косинуса упрощаются:
Окружность с центром в начале координат и радиусом, равным единице, называется единичной окружностью.
Отсюда получаем определения синуса и косинуса на единичной окружности.
Синусом угла α называется ордината точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.
Косинусом угла α называется абсцисса точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.
Применив определения тангенса и котангенса острого угла в прямоугольном треугольнике в ∆AOB, получаем:
Приходим к определению тангенса и котангенса на единичной окружности.
Тангенсом угла α называется отношение ординаты точки A единичной окружности к абсциссе этой точки.
Котангенсом угла α называется отношение абсциссы точки A единичной окружности к ординате этой точки.
Видео:Изобразить на единичной окружности точку.Скачать

One Comment
Искала везде. Нигде нет такого подробного и понятного объяснения. Огромное Вам спасибо!
💥 Видео
ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Тема 1. Единичная окружность. Градусная и радианная мера произвольного угла. Определение синуса и тдСкачать

ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ: любого аргумента, угла α, единичная и числовая окружностьСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать

Синус, косинус, тангенс, котангенс. Тригонометрия #3Скачать

Синус и косинус на единичной окружности. ПримерСкачать

Урок 29 (осн). Задачи по теме "Плотность" - 1Скачать

№1018. Угол между лучом ОА, пересекающим единичную полуокружность, и положительной полуосью ОхСкачать
Период синуса и косинуса в градусах. В какой четверти находится угол поворота. 8-11 класс.Скачать

ПОСТРОЕНИЕ УГЛА ПО ДАННОМУ ЗНАЧЕНИЮ ЕГО ТРИГОНОМЕТРИЧЕСКОЙ ФУНКЦИИСкачать