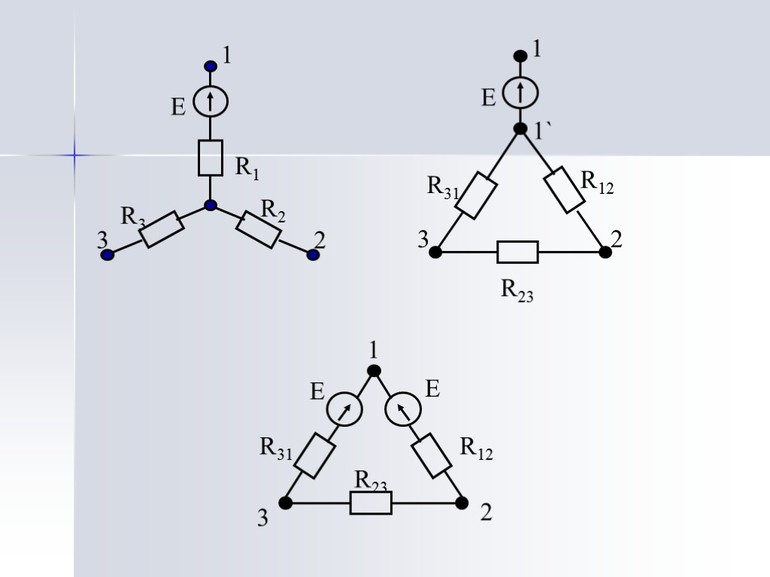
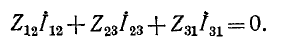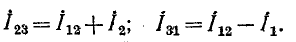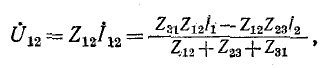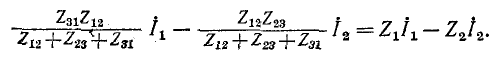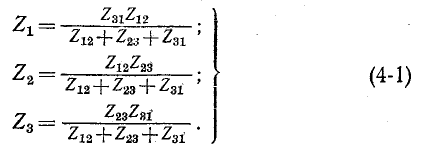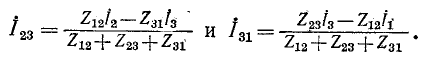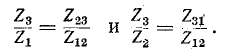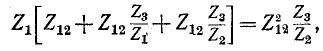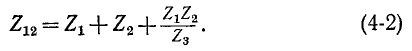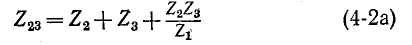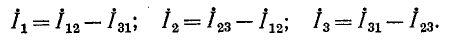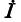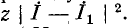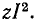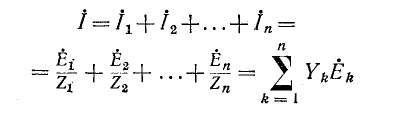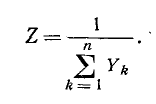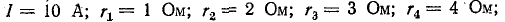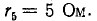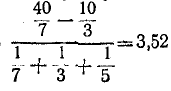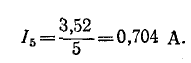Пусть требуется рассчитать цепь, показанную на рис. 7.1, а.
Рис. 7.1 — Преобразования электрической цепи
Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.
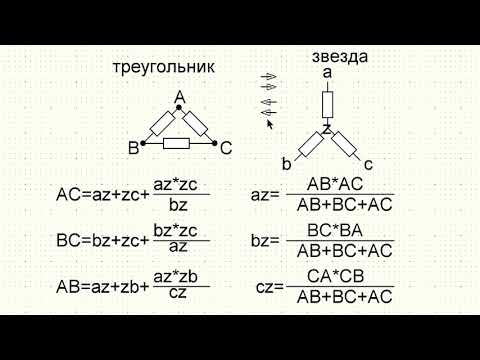
Треугольник и звезда сопротивлений имеют вид, показанный на рис. 7.2.
Рис. 7.2 — Треугольник и звезда сопротивлений
Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.
Можно показать, что условием эквивалентности являются следующие уравнения:
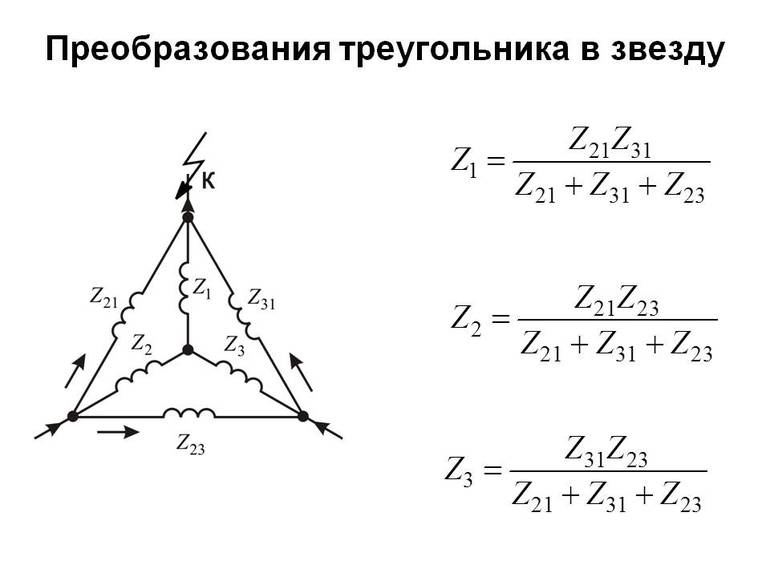
а) при преобразовании треугольника в звезду:
б) при преобразовании звузды в треугольник:
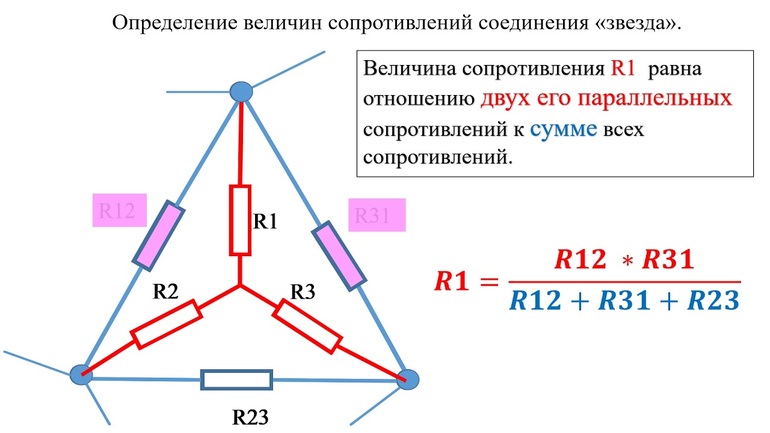
Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.
При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R3.
Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.
а) Решение преобразованием треугольника в звезду.
Теперь общее сопротивление цепи легко находится:
Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен:
Токи в паралельных ветвях:
Возвращаемся к исходной схеме (рис. 7.1, а):
Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A. Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.
б) Решение преобразованием звезды в треугольник.
Преобразуем звезду, образуемую в схеме на рис. 7.1, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 7.1, в).
Определяем сопротивления треугольника:
Теперь рассчитываем преобразованную цепь. Сначала находим эквивалентные сопротивления участков ac и cd:
Затем определяем общее сопротивление и токи:
Возвращаемся к исходной схеме:
Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.
- Преобразование треугольника в звезду — методы, формулы и примеры
- Общие сведения
- Переход треугольник — звезда
- Обратное преобразование
- Решение примера
- Преобразование схем электрических цепей
- Последовательное соединение
- Параллельное соединение
- Смешанное соединение
- Эквивалентные участки цепи с последовательным и параллельным соединениями
- Преобразование треугольника в эквивалентную звезду
- Преобразование звезды в эквивалентный треугольник
- Эквивалентные источники э. д. с. и тока
- Преобразование схем с двумя узлами
- Перенос источников в схеме
- Преобразование симметричных схем
- 🔥 Видео
Видео:Задача на расчет эквивалентного сопротивления цепиСкачать

Преобразование треугольника в звезду — методы, формулы и примеры
Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Общие сведения
Электрическая цепь предназначена для обеспечения протекания по ней токов определённой величины. Она содержит источники и приёмники энергии, которые соединены проводниками. При изображении радиоэлементов используют их графические обозначения. Электрические же соединения обозначают прямыми линиями. Замкнутые проводники образовывают контуры. В их состав входят узлы (точки контакта трёх и более линий) и ветви (соединители).
Существует 2 способа обеспечения контакта между элементами:
- параллельный — при таком включении в цепи не будет ни одного узла;
- последовательный — входящие в цепь эквиваленты присоединены к одной точке, связанной или не имеющей контакта с другой.
В основе преобразований лежит приведение схемы к упрощённому виду без изменения величины тока или напряжения. Для этого выделяют один контур и заменяют его эквивалентным сопротивлением. При последовательном соединении импеданс просто складывают, а вот при параллельном используют формулу: 1/R = 1/R1 + 1/R2 +…1/Rn.
Таким образом, путем замены пары элементов одним, схема последовательно упрощается до тех пор, пока в ней не окажется один резистор. А уже по его величине и рассчитывают ток цепи. Но в некоторых случаях существуют соединения, которые не поддаются методу упрощения. Если внимательно посмотреть на такую цепь, можно увидеть подключение, похожее на треугольник. В таком случае невозможно определить, какие элементы параллельные, а какие последовательные.
Чтобы найти эквивалентное сопротивление таких сложных соединений, используют преобразование треугольника в равнозначную звезду. По сути, при треугольном подключении 3 элемента образуют замкнутый контур. При этом между каждой парой резисторов имеется узел. Связь же звездой образуется при получении трёх лучевого соединения, в котором каждый элемент цепи подсоединён одним концом к общему узлу, а другой стороной контакта к остальной части схемы.
Преобразование в физике выполняют по строго установленным формулам.
Если его выполнить правильно, значения потенциалов в одноимённых точках треугольника и звёзды, а также подводящиеся к этим узлам токи, останутся одинаковыми. Это значит, что вся оставшаяся часть схемы «не заметит» выполненной замены.
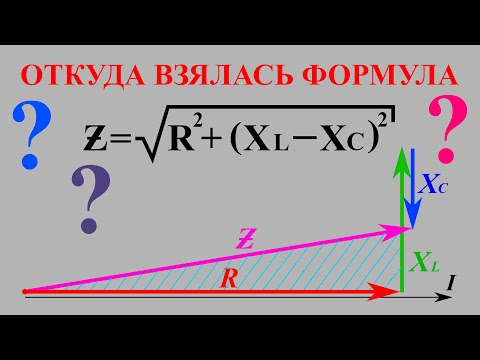
Видео:Откуда взялась формула полного сопротивления цепи? Треугольник напряжений, треугольник сопротивленийСкачать
Переход треугольник — звезда
Чтобы преобразовать треугольник в звезду, нужно применять особый подход. Закон Ома для такого случая применить невозможно, поэтому упрощения выполняют, руководствуясь правилами Киргофа. Их 2. Первое гласит, что в узле токи компенсируют друг друга, то есть их алгебраическая сумма равняется нулю. Второе же сообщает, что если сложить электродвижущую силу в любом замкнутом контуре цепи, она будет равна алгебраической сумме падений потенциала на импедансе этой части схемы.
В соответствии с этими законами, можно утверждать, что в узлах электрического заряда нет. Он не расходуется и не собирается. В количественном виде первое утверждение записывают так: I1 = I2 + I3, где с левой стороны стоит значение тока втекающего, а справа вытекающих. Второй закон описывается выражением: E1 — Е2 = -UR1 — UR2 или E1 = Е2 — UR1 — UR2.
Опираясь на эти правила, можно выполнить перевод схемы.
Сделать это удобно, руководствуясь следующим алгоритмом:
- Пусть имеется контур, образованный из резисторов Ra1, Rb1, Rc1, соединённых треугольником.
- Сумму всех сопротивлений можно обозначить символом RΔ. Её можно будет найти, сложив все импедансы: RΔ = Ra1 + Rb1 + Rc1.
- Для получения равенства с неизвестными нужно сделать перестановку в соотношении. Выражение примет вид: Ra2 + (RΔs)Rb2 + (RΔs)Rc2 = Ra1 * Rb1 + Rb1 * Rc1.
- Из эквивалентных уравнений можно вывести ещё 2 формулы, описывающие оставшиеся пары контактов. Беря во внимание симметрию, можно получить: Ra2 + (0)Rb2 + (RΔs)Rc2 = Ra1 * Rс1 + Rb1 * Rc1 и Ra2 + (RΔs)Rb2 + (0)Rc2 = Ra1 * Rc1 + Ra1 * Rb1.
- Нужно выполнить сложение последних двух уравнений, а после, отняв первое, получить равенство: 2 (RΔs) * Ra2 = 2 * Ra1 * Rc1. Отсюда: Ra2 = Ra1 * Rc1 / RΔs.
- По аналогии можно найти и оставшиеся эквиваленты: Rb2 = Ra1 * Rb1 / RΔs и Rc2 = Rc1 * Rb1 / RΔs.
Конечно же, при решении задачи о переводе из одного вида подключения в другое никто не расписывает промежуточные вычисления, а используют сразу конечную формулу: Rk = Rk1 * Rk2 / RΔs, где: Rk — сопротивление, подключённое к контакту в уже трансформированной схеме, а Rk1 и Rk2 — резисторы, стоящие в контуре типа треугольник.
Таким образом, сопротивление, соединённое с каждым узлом при переходе, можно найти из перемножения сопротивлений, подключённых к соответствующей точке в цепи, подключённой треугольником, и дальнейшему их делению на сумму всех резисторов в неизменном контуре.
Видео:Физика - Электричество. Найти общее сопротивление цепи 1Скачать

Обратное преобразование
Чтобы получить нужную формулу, следует вести ряд обозначений. Токи, подходящие к узлам, можно обозначить как I1, I2, I3. Преобразование должно выполняться таким образом, чтобы при замене контура величины других токов и потенциалов не изменялись. Для этого следует выразить упорядоченное движение зарядов через напряжение точек и проводимость.
В соответствии с первым правилом Кирхгофа, можно записать: I1 + I2 + I3 = 0. Равенство можно изменить так: (f1 — f0) * p1 + (f2 — f0) * p1 + (f2 — f0) * p1 = 0, где: f — потенциал в точке. В выражении легко выполнить простые преобразования и найти f0. Оно будет равно: f0 = (f1p1 + f2p2 + f3p3) / (p1 + p2 + p3). Полученную формулу возможно использовать для вывода тока. Для I1 будет верным уравнение: I1 = (f1 — f0) * p1 = (f1 * (p2 + p3) — f2 * p2 — f3p3) * p / (p1 + p2 + p3).
Движение заряда удобно обозначать не буквами, а цифрами. Например, число 12 будет показывать, что рассматривается связь первого и второго узла. Таким образом, в треугольнике I1 = I12 — I31 = (f1 — f2) * p12 — (f3 — f1) * p13 = f1* (p12 + p13) — f3p13 -f 2p12.
Учитывая, что ток I1 в схеме треугольник и звезда одинаков, при этом величины потенциалов не влияют на его значение, коэффициенты, стоящие возле f в правой и левой части, будут равны. Тогда можно записать следующие равенства: p12 = p1 * p2 / (p1 + p2 + p3); p13 = p1 * p3 / (p1 + p2 + p3); p23 = p2 * p2 / (p1 + p2 + p3). Как раз по этим формулам и возможно рассчитать проводимость треугольника через звезду.
Зная проводимость, можно определить импеданс, так как это величина обратна сопротивлению. Вывод формулы будет иметь следующий вид: R12 = (1/r1 + 1/r2 + 1/r3) / 1/r1 * r2. Для дальнейших расчётов многочлен (1/r1 + 1/r2 + 1/r3) удобно заменить одной буквой, например, s. Тогда: R12 = s / r3; R23 = s / r1; R13 = s / r2. Подставив последние выражения в формулу для нахождения s, можно будет получить отношение: m = (r12 * r23 * r31) / (r12 + r23 + r31).
Формулы для нахождения эквивалента при переходе примут вид:
- R1 = (r12 * r31) / y;
- R2 = (r23 * r12) / y;
- R3 = (r13 * r23) / y.
Где: y = r12 + r23 + r31. Полезность преобразования в треугольник позволяет привести схему к набору простых последовательных соединений. Подключение двигателей по этой схеме позволяет добиться наибольшей отдачи мощности, например, при модернизации промышленных электросетей.
Видео:Как легко рассчитать сопротивление цепейСкачать

Решение примера
При знании формул решение задач на преобразование треугольника в звезду или обратно обычно не доставляет проблем. Нужно просто внимательно следить за подставляемыми величинами. Но перед тем как приступить непосредственно к расчёту эквивалентной схемы, следует оценить необходимость выполнения такого действия. Некоторые элементы могут быть соединены последовательно или параллельно, поэтому нужно будет начать с простых преобразований, а уже позже переходить к звезде или треугольнику.
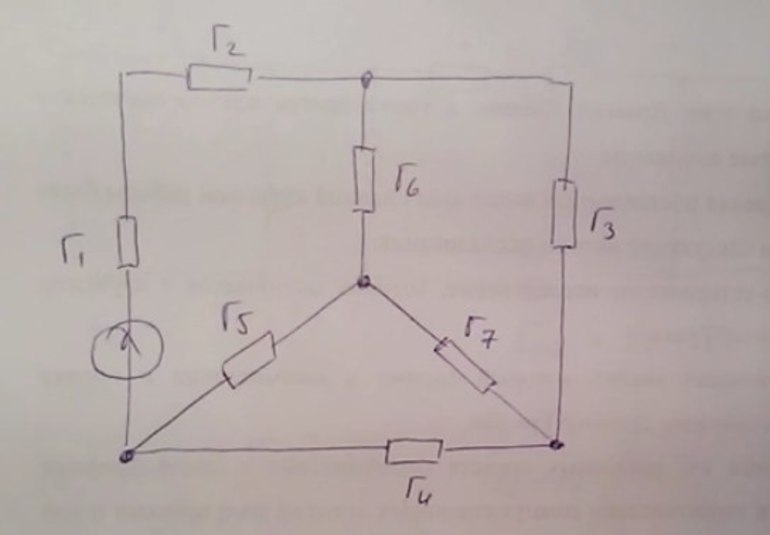
Вот пример задания. Имеется трёхфазная цепь. Посчитать её эквивалентное сопротивление. Известно, что схема подключена к источнику напряжения 220 вольт, сопротивление: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 50 Ом, R6 = 60 Ом, R7 = 70 Ом.
В этой схеме сопротивления R1 и R2 соединены последовательно. Что же касается остальных элементов, сказать, какой тип подключения у них по отношению друг к другу, нельзя. Но зато видно, что контур, состоящий из R5, R7, R4, является треугольником, то есть задача состоит в превращении его в эквивалентную трёхлучевую звезду.
Новые элементы можно обозначить как R57, R45, R47. Чтобы найти номиналы новых сопротивлений, нужно воспользоваться эквивалентными формулами. R57 = (R5 * R7) / R5 + R4 + R7 = 50 * 70 / 50 + 40 + 70 = 3500 / 160 = 21,8 Ом; R45 = (R4 * R5) / R5 + R4 + R7 = 40 * 50 / 50 + 40 + 70 = 2000 / 160 = 12,5 Ом; R47 = (R4 * R7) / R5 + R4 + R7 = 40 * 70 / 50 + 40 + 70 = 2800 / 160 = 17,5 Ом.
Теперь эквивалентный контур можно подставить в схему вместо треугольника. В результате цепь будет состоять из трёх последовательно соединённых резисторов R1, R2 и R45. Общий импеданс для них будет равен: Rx = R1 + R2 + R45 = 10 + 20 + 17,5 = 47,5 Ом. Аналогично можно вычислить параметр и для второго контура: Ry = R6 + R57 = 60 + 21,8 = 81,8 Ом. Останется найти сопротивление ветви, включающую R3 и R47, Rz = R3 + R47 = 30 + 17,5 = 47,5 Ом.
Теперь схема принимает довольно простой вид. Контур состоит из трёх включённых параллельно относительно друг друга резисторов Rx, Ry, Rz. Если использовать формулу нахождения эквивалента для такого типа включения, результирующее первое сопротивление будет равно: Rоб = Ry * Rz / (Ry + Rz) = 81,8 * 47,5 / (81,8 + 47,5) = 3885,5 / 129,3 = 30,05 Ом. Теперь схема уже стала одноконтурной и содержит соединение, которое будет называться последовательным.
Таким образом, эквивалентное сопротивление для схемы будет составлять: Rx + R об = 30,05 + 47,5 = 77,55 Ом. Задача решена.
Видео:Найти общее сопротивление цепи со смешанным соединением резисторовСкачать

Преобразование схем электрических цепей
Содержание:
Преобразование схем электрических цепей:
При расчете электрических цепей часто возникает целесообразность преобразования схем этих цепей в более простые и удобные для расчета. Так, при одном или нескольких источниках электрической энергии в ряде случаев удается преобразовать электрическую схему в одноконтурную или в схему с двумя узлами, что весьма упрощает последующий расчет.
Описываемые ниже приемы преобразования схем электрических цепей применимы для цепей постоянного и переменного тока-, ради общности изложения они приводятся в комплексной записи.
Одним из основных видов преобразования электрических схем, часто применяемых на практике, является преобразование схемы со смешанным соединением элементов. Смешанное соединение элементов представляет собой сочетание более простых соединений — последовательного и параллельного, рассмотрению которых и посвящен данный параграф.
Видео:урок 3 - Нахождение эквивалентного сопротивления сложной схемыСкачать

Последовательное соединение
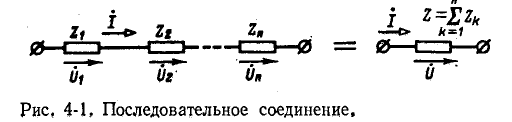
На рис. 4-1 изображена ветвь электрической цепи, в которой последовательно включены комплексные сопротивления
Напряжения на отдельных участках цепи обозначены через
По второму закону Кирхгофа
Сумма комплексных сопротивлений всех последовательно соединенных участков цепи
называется эквивалентным комплексным сопротивлением.
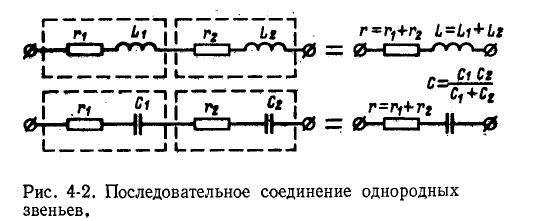
Если мнимые части комплексов
представляют собой сопротивления одинакового характера— индуктивного или емкостного (рис. 4-2), то эквивалентное комплексное сопротивление Z находится в результате
арифметического сложения в отдельности сопротивлений 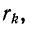
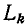
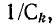
где 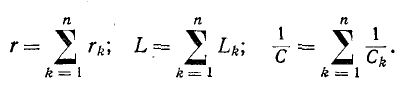
Ток в цепи равен:
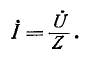
Напряжения на участках цепи, соединенных последовательно, относятся как комплексные сопротивления этих участков: напряжение на k-м участке равно произведению суммарного напряжения 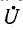
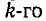
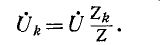
Приведенные выше формулы справедливы при любых значениях
Видео:R, L, C в цепи переменного тока/Треугольник сопротивлений/Сдвиг по фазеСкачать

Параллельное соединение
На рис. 4-3 изображена схема электрической цепи с двумя узлами. Между этими узлами параллельно соединены ветви с комплексными проводимостями 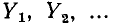
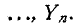
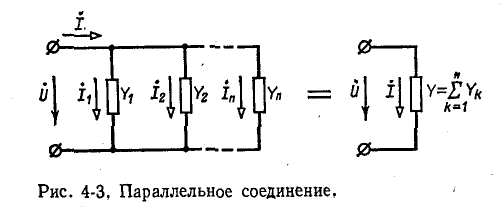
Токи в ветвях обозначены через
По первому закону Кирхгофа
Сумма комплексных проводимостей всех ветвей, соединенных параллельно,
называется эквивалентной комплексной проводимостью.
Если мнимые части комплексов 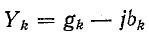
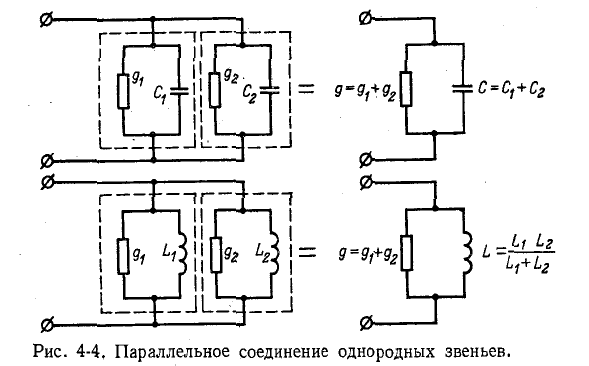
комплексная проводимость Y находится в результате арифметического сложения отдельных активных проводимостей 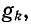
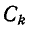
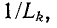
Суммарный ток в цепи равен:
Токи в ветвях относятся, как их комплексные проводимости: ток в 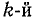
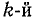
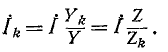
Данным выражением особенно удобно пользоваться при n > 2. При этом значения 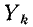
В случае параллельного соединения двух ветвей (n = 2) обычно пользуются выражениями, в которые входят сопротивления 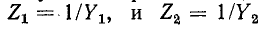
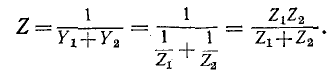
Токи в параллельных ветвях:
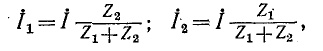
t. e. ток одной из двух параллельных ветвей равен суммарному току, умноженному на сопротивление другой ветви и деленному на сумму сопротивлений обеих ветвей.
Видео:8 класс, 20 урок, Смешанное соединение проводниковСкачать

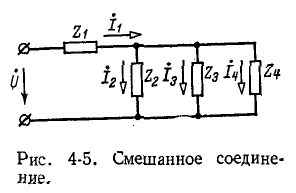
Смешанное соединение
Электрические схемы, имеющие смешанное соединение, могут быть преобразованы в более простую электрическую схему путем замены параллельных ветвей одной ветвью и соответственно последовательно соединенных участков цепи — одним участком.
На рис. 4-5 показан пример электрической цепи со смешанным соединением. Эта схема легко приводится к одноконтурной. Первоначально вычисляется эквивалентная комплексная проводимость параллельных ветвей; затем находится величина, обратная проводимости, т. е. общее комплексное сопротивление параллельных ветвей; найденное комплексное сопротивление суммируется с комплексным сопротивлением последовательно включенного участка. Полученное суммарное
комплексное сопротивление эквивалентно сопротивлению исходной цепи со смешанным соединением.
Расчетные выражения для рассматриваемого случая будут следующие:
Суммарное комплексное сопротивление всей цепи равно:
а суммарный ток 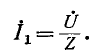
Токи в ветвях относятся, как комплексные проводимости ветвей:
Таким юбразом, многоконтурная электрическая схема со смешанным соединением приводится к одноконтурной, 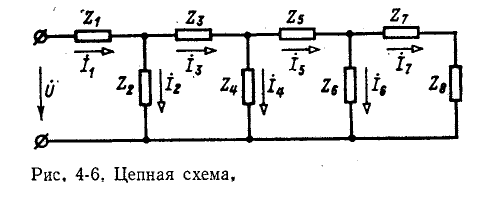
имеющей суммарное комплексное сопротивление Z или соответственно суммарную комплексную проводимость Y. Распределение токов и напряжений в смешанной цепи подчиняется правилам, указанным в предыдущем параграфе.
Описанный выше порядок преобразования схемы и нахождения распределения токов принципиально применим и для так называемой цепной схемы, показанной на рис. 4-6. Просуммировав комплексные сопротивления 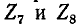
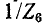
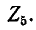
таким образом дальше, получим в итоге результирующее комплексное сопротивление цепи и соответственно суммарный ток 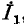
Однако такой способ расчета цепной схемы является достаточно трудоемким и утомительным. Более целесообразно в этом случае воспользоваться другим методом, который известен под названием метода подобия или единичного тока.
Задавшись током в последней ветви, равным единице 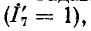
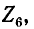
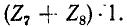
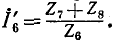
Прибавив к напряжению на 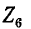
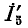
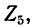
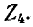
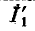
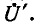
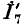
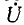
Видео:как решать задачи со сложными схемамиСкачать

Эквивалентные участки цепи с последовательным и параллельным соединениями
Обозначим комплексное сопротивление участка цепи, состоящего из двух последовательно соединенных элементов, через 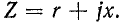
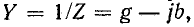
Если два элемента с проводимостями g и b, вычисленными по этим формулам, соединить параллельно, то суммарная комплексная проводимость будет равна Y и соответственно комплексное сопротивление будет равно Z,
Такие две цепи с последовательным и параллельным соединениями, имеющие одинаковые сопротивления на выводах, называются эквивалентными.
Ввиду того что реактивное сопротивление х, входящее в расчетные формулы, в общем случае зависит от частоты, условие эквивалентности этих цепей выполняется только при той частоте, для которой вычислено х.
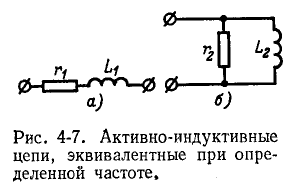
Пусть, например, задана схема с последовательным соединением сопротивления 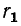
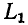
Активная и реактивная проводимости исходной цепи:
Из условия эквивалентности цепей следует, что параметры новой цепи будут:
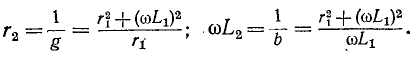
Вычислив по этим формулам 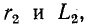
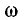
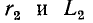
При 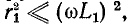
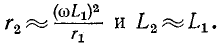
Если исходной является схема рис. 4-7, б и заданными параметрами являются 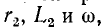
Из полученных выражений видно, что числовые значения 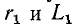
Условия эквивалентности для цепей с последовательным и параллельным соединением сопротивления и емкости имеют вид: 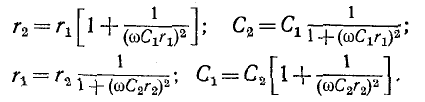
При достаточно высокой частоте 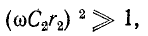
Видео:Лекция 24. Преобразование треугольника в звезду.Скачать

Преобразование треугольника в эквивалентную звезду
Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи
сохраняются неизменными. Иначе говоря, эквивалентность треугольника и звезды понимается в том смысле, что при одинаковых напряжениях между одноименными выводами токи, входящие в одноименные выводы, одинаковы. Это равносильно тому, что мощности в этих цепях одинаковы.
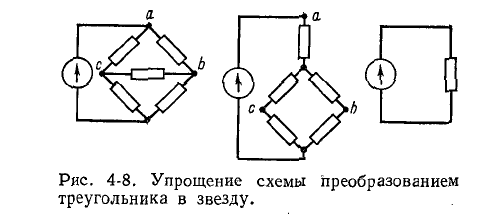
На рис. 4-8 показан случай, когда преобразование треугольника в эквивалентную звезду дает возможность преобразовать многоконтурную схему в одноконтурную.
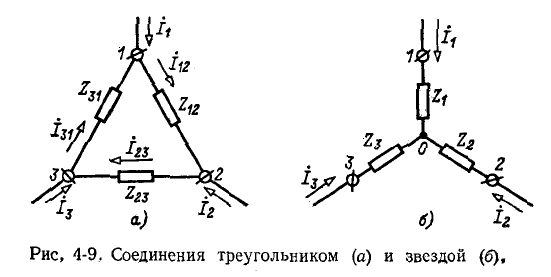
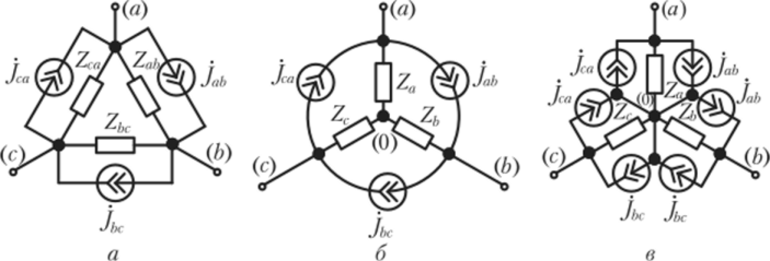
Для вывода расчетных выражений, служащих для преобразования треугольника в эквивалентную звезду, ниже приняты следующие обозначения (рис. 4-9):
— сопротивления сторон треугольника;
— сопротивления лучей звезды;
— токи, подходящие к выводам 1, 2, 3
— Токи в ветвях треугольника.
Выразим токи в ветвях треугольника через приходящие токи.
По второму закону Кирхгофа сумма напряжений в контуре треугольника равна нулю:
По первому закону Кирхгофа для узлов 2 и 1
Решение этих уравнений относительно 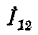
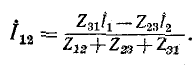
Напряжение между выводами 1 и 2 схемы рис. 4-9, а будет:
a в схеме рис. 4-9, б оно равно: 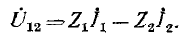
Для эквивалентности необходимо равенство напряжений 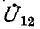
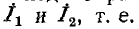
Это возможно при условии:
Третье выражение получается в результате круговой замены индексов.
Итак, комплексное сопротивление луча звезды равно произведению комплексных сопротивлений прилегающих сторон треугольника, деленному на сумму комплексных сопротивлений трех сторон треугольника.
Выше было получено выражение для тока в стороне 1—2 треугольника в зависимости от токов 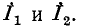
Видео:Соединение обмоток треугольникомСкачать

Преобразование звезды в эквивалентный треугольник
В расчетах также возникает необходимость замены звезды эквивалентным треугольником. На рис. 4-10 показан, например, случай, когда такая замена позволяет
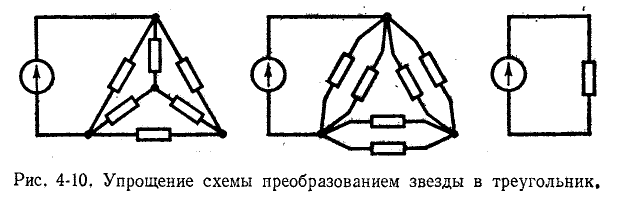
преобразовать сложную электрическую схему в одноконтурную.
При переходе от звезды к треугольнику заданными являются сопротивления звезды 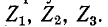
Деление третьего уравнения на первое, а затем на второе дает:
Выражая отсюда 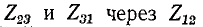
Аналогично круговой заменой индексов получим:
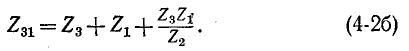
Отедовательно, комплексное сопротивление стороны треугольника равно сумме комплексных сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.
Токи в лучах звезды легко выражаются через токи в сторонах треугольника. С учетом положительных направлений на рис. 4-9 имеем:
Видео:Метод эквивалентных преобразований. Как находить токи и напряжения в цепиСкачать
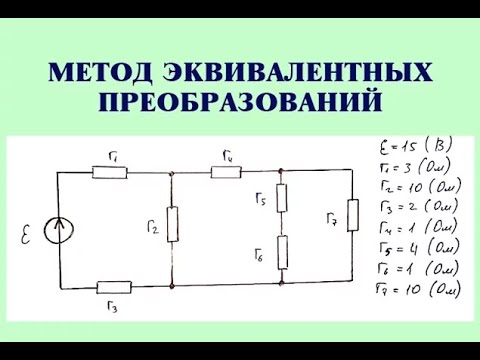
Эквивалентные источники э. д. с. и тока
Два разнородных источника электрической энергии — источник э. д. с. и источник тока — считаются эквивалентными,, если при замене одного источника другим токи и напряжения во внешней электрической цепи, с которой эти источники соединяются, остаются неизменными. На рис. 4-11 изображены эквивалентные источники тока, посылающие во внешнюю цепь ток 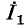
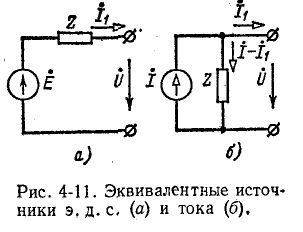
Условием эквивалентности источников, именуемым в дальнейшем правилом об эквивалентных источниках э.д.с. и тока, служит следующее соотношение между э. д. с. Ё источника э. д. с. и током
где Z — внутреннее комплексное сопротивление как источника э. д. с., так и источника тока.
Действительно, напряжение 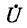
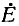
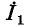
Соответственно напряжение 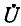
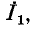
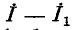
В обоих случаях напряжения на выводах обоих источников одинаковы:
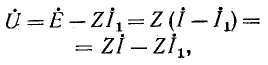
т. е. получается условие (4-3), не зависящее от тока 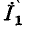
При отсоединении эквивалентных источников э. д. с.
и тока от внешней цепи 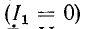
Следует заметить, что мощности, расходуемые во внутренних сопротивлениях эквивалентных источников э. д. с. и тока, неодинаковы. В первом случае полная мощность, расходуемая в источнике, равна 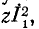
Например, при отсоединении источников от внешней цепи в первом случае мощность в источнике не расходуется, а во втором случае она составляет
Поэтому эквивалентность источников следует понимать только в смысле неизменности токов, напряжений и мощностей во внешней электрической цепи, присоединенной к источникам.
Если внутреннее сопротивление источника э. д. с. равно нулю, то непосредственное применение формулы (4-3) для нахождения эквивалентного источника тока по, заданной э. д. с. источника не представляется возможным. В таких случаях сопротивление внешней цепи, включенной последовательно с э. д. с., можно рассматривать в качестве внутреннего сопротивления источника, что позволит применить формулу (4-3).
В случае сложной электрической цепи замена источника э. д. с. эквивалентным источником тока или обратно может иногда упростить расчет.
Целесообразность такой замены проиллюстрирована, в частности, в следующем параграфе.
Видео:8 класс, 21 урок, Расчет электрических цепейСкачать

Преобразование схем с двумя узлами
Применим правило об эквивалентных источниках э. д. с. и тока к преобразованию схемы с параллельным соединением n ветвей, содержащих источники э. д. с. (рис. 4-12, а).
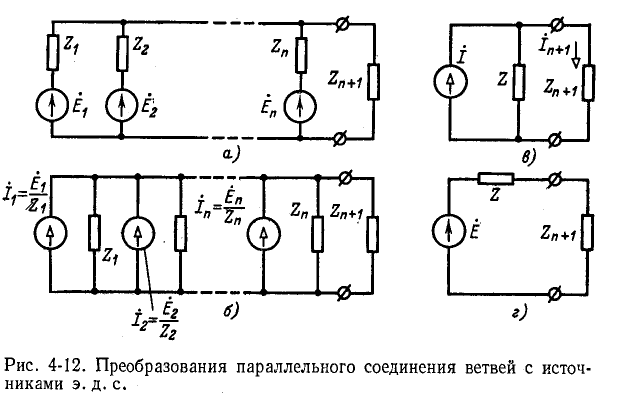
Заменяя заданные источники э. д. с. источниками тока, получаем схему рис. 4-12, б. Источники тока в совокупности образуют эквивалентный источник тока 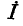
Пользуясь этим соотношением, можно в конечном итоге перейти от схемы рис. 4-12, в к схеме рис. 4-12, s, являющейся эквивалентом исходной схемы рис. 4-21, а. Здесь 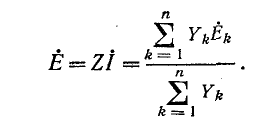
Таким образом, n параллельных ветвей с источниками э. д. с. между двумя узлами могут быть заменены одним источником тока (рис. 4-12, в) или источником э. д. с. (рис. 4-12, s).
Ток во внешней цепи (в ветви с сопротивлением 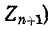
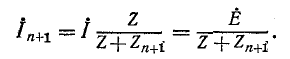
Напряжение между двумя узлами находится по формуле
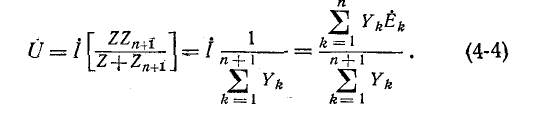
Выведенные здесь выражения широко используются для расчета электрических цепей с двумя узлами, а также более сложных цепей, приводящихся к двум узлам.
Видео:урок 2 Преобразование треугольника сопротивлений в звездуСкачать

Перенос источников в схеме
Расчет электрической цепи облегчается в ряде случаев в результате переноса в схеме источников э. д. с. или тока. Как это видно из уравнений Кирхгофа, токи в схеме определяются заданными величинами суммарных э. д. с. в контурах независимо от того, из каких отдельных слагающих они состоят. Поэтому изменение расположения в схеме источников э. д. с., при котором суммарные э. д. с. во всех контурах сохраняются неизменными, не влияет на токи в ветвях. Аналогично напряжения на ветвях определяются заданными суммарными токами источников тока в узлах, и поэтому изменение расположения в схеме источников тока, при котором их суммарные токи во всех узлах сохраняются неизменными, не влияет на напряжения в схеме.
Если, например, требуется исключить источник э. д. с. из какой-либо ветви, то в данную ветвь вводится компенсирующая э. д. с., причем точно такая же э. д. с. вводится одновременно во все остальные ветви, сходящиеся
в одном из узлов данной ветви. Компенсирующая и дополнительные э. д. с. имеют одинаковое направление по отношению к рассматриваемому узлу. В результате этого источник э. д. с. из ветви исключается и появляются источники э. д. с. в других ветвях схемы. Суммарные э. д. с. во всех контурах и соответственно токи в ветвях остаются прежними.
Итак, источник э. д. с. может быть перенесен из какой-либо ветви схемы во все другие ветви, присоединенные к узлу данной ветви, без изменения токов в схеме.
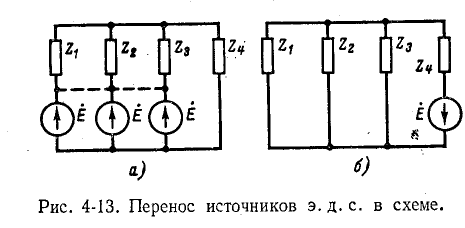
Справедливо и обратное положение: если во всех ветвях, кроме одной, сходящихся в узле, имеются одинаковые источники э. д. с. (рис. 4-13, а), направленные все к одному узлу или все от узла, то они могут быть заменены одним источником э. д. с. в ветви, в которой источник отсутствовал (рис. 4-13, б).
Это положение подтверждается тем, что суммарные э. д. с. в контурах схем на рис. 4-13, а и б одинаковы.
Имеется и другое доказательство данного положения: ввиду равенства э. д. с. всех источников вторые выводы
их могут быть объединены, как имеющие одинаковый потенциал. В результате такого объединения, показанного на рис. 4-13, а пунктиром, получается схема рис. 4-13, б.
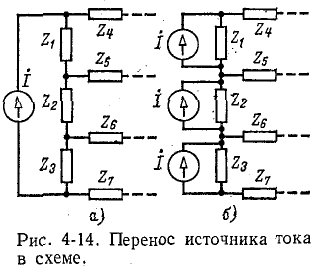
В случае переноса источников тока они присоединяются к узлам схемы так, чтобы оставались неизменными их суммарные токи в узлах.
Так, например, несмотря на то, что источники тока размещены в схемах рис.
4-14, а и б различно, суммарные токи источников в узлах обеих схем одинаковы. Поэтому и напряжения между узлами не изменились.
Итак, источник тока может быть заменен источниками тока, подключенными. параллельно всем
ветвям, которые составляли контур с рассматриваемым источником.
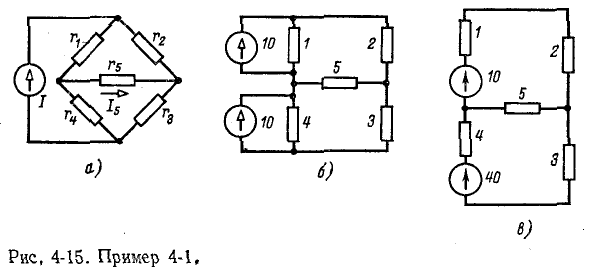
• Перенос источников в схеме успешно сочетается на практике с различными методами преобразований и расчетов (см. пример 4-1).
Пример 4-1.
Вычислить ток в диагональной ветви 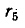
Дано:
Заданный источник тока может быть заменен двумя источниками, подключенными параллельно сопротивлениям 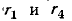
Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Преобразование симметричных схем
Схема электрической цепи, в которой имеется ось симметрии, называется симметричной. Например, схема рис. 4-16, а симметрична относительно вертикальной оси. В симметричных схемах легко выявляются точки или узлы с одинаковым потенциалом. В ветвях, присоединенных к таким узлам, токи равны нулю. Поэтому эти ветви
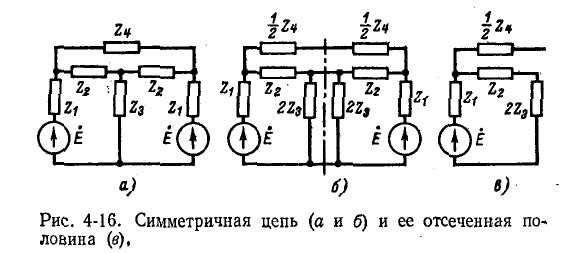
можно разрезать, не нарушая распределения токов и напряжений в схеме. Точки, имеющие одинаковый потенциал, могут быть объединены. Рассечение ветвей, по которым не проходит ток, и объединение точек равного потенциала упрощают схему и облегчают расчет.
Так, в симметричной схеме рис. 4-16, б токи в соединениях, пересекающих ось симметрии, отсутствуют. Разрезав схему по оси симметрии, получим с обеих сторон одноконтурную схему рис. 4-16, в, которая легко рассчитывается.
Допустим теперь, что полярность источников в симметричной схеме неодинакова (рис. 4-17, а). В этом случае (равенство э. д. с. источников и различие их полярности) токи в симметричных ветвях (например, 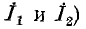
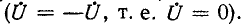
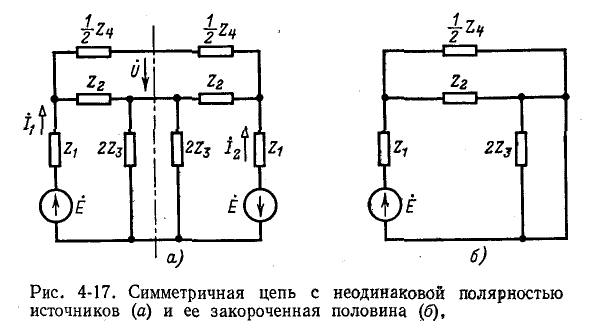
Таким образом, расчет сложных симметричных схем приводится к расчету более простых схем.
На рис. 4-18, а и б показана симметричная мостовая схема, имеющая две оси симметрии — вертикальную и
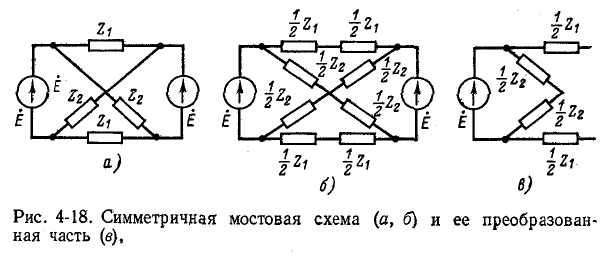
горизонтальную. В продольных ветвях ток отсутствует; потенциалы средних точек поперечных (перекрещенных) ветвей одинаковы.
Поэтому продольные ветви могут быть рассечены, а средние точки поперечных ветвей — объединены. В результате с обеих сторон получится одноконтурная схема (рис. 4-18, в), расчет которой крайне прост.
Если изменить полярность одного из источников (рис. 4-19, а), то роли продольных и поперечных ветвей поменяются и преобразованная часть схемы примет вид, показанный на рис. 4-19, б.
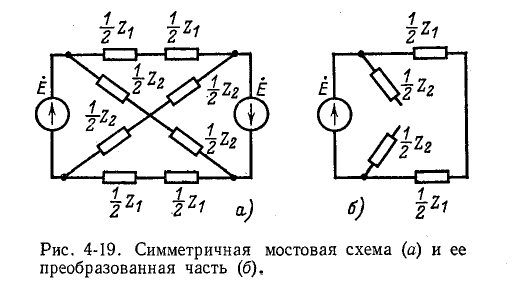
В разобранных выше примерах э. д. с. источников были равны. В случае неравенства э. д. с. источников преобразование симметричной схемы удобно сочетается с методом наложения (см. пример 7-5).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Установившиеся процессы в линейных электрических цепях
- Методы расчета простых электрических цепей
- Метод сигнальных графов
- Электрическая ёмкость и ее расчет
- Топологии электрических цепей
- Уравнения электрического равновесия цепей
- Линейные цепи при гармоническом воздействии
- Нелинейные резистивные цепи
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔥 Видео
Звезда,треугольник соединение сопротивленийСкачать
8 класс. Смешанное соединение проводников. II вариант.Скачать

Мощность трехфазного напряжении при подключении нагрузки звездой и треугольникомСкачать

Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать














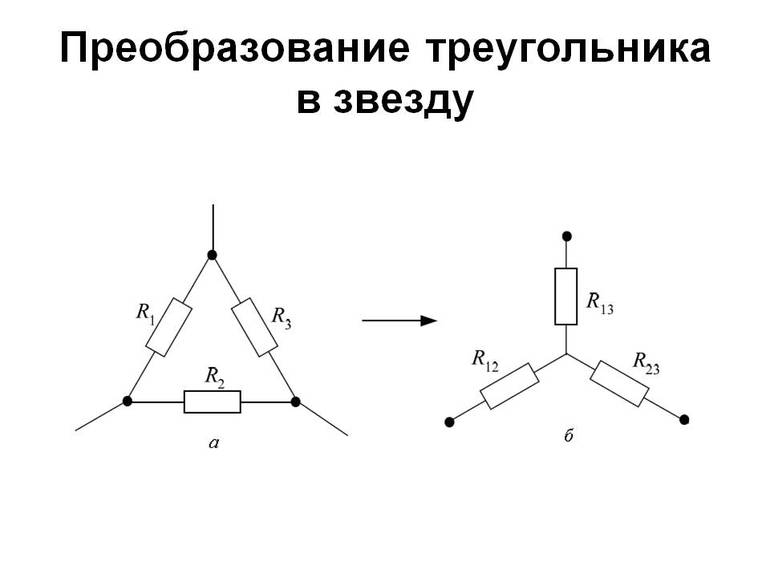

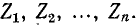
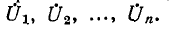
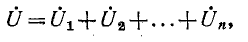
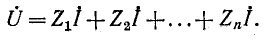
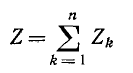
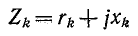
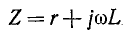
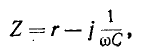
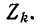
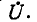
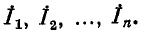
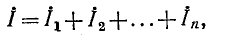
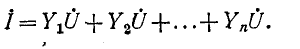
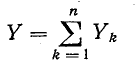
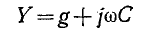
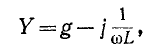
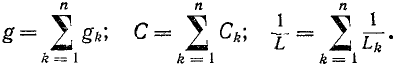
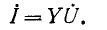
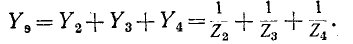
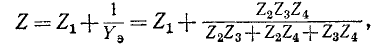
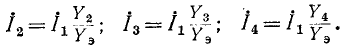
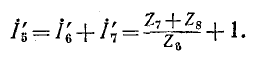
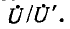
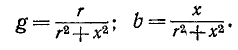
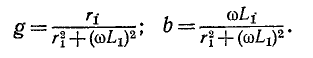
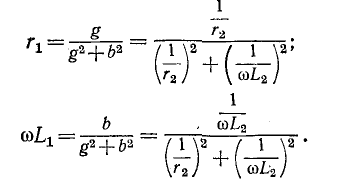
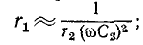
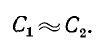
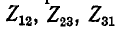 — сопротивления сторон треугольника;
— сопротивления сторон треугольника;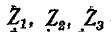 — сопротивления лучей звезды;
— сопротивления лучей звезды;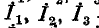 — токи, подходящие к выводам 1, 2, 3
— токи, подходящие к выводам 1, 2, 3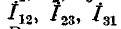 — Токи в ветвях треугольника.
— Токи в ветвях треугольника.