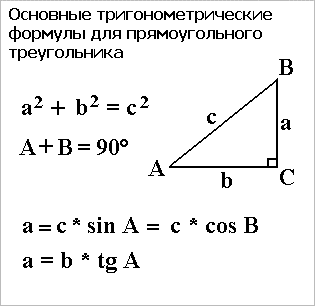Оценка расстояния до объекта важна в повседневной жизни, походах и ситуациях выживания. Это помогает рассчитать расстояние и оценить время в пути.
Оценка расстояния с помощью пальца основана на известном факте об анатомии человека: длина руки человека примерно в десять раз больше расстояния между его глазами. Помните о золотом сечении Фибоначчи?
- Условия задачи и исходные данные
- Определение расстояния по деревьям
- Определение по шагам человека
- Как это работает
- Как определить расстояние по звуку и глазомером
- Простые способы измерения расстояний и высот на местности
- Прямые методы определения линейных расстояний
- Определение расстояний по угловой величине известных предметов
- Определение высоты столба с помощью вращающейся планки
- Высокоточные измерения расстояний
- 🌟 Видео
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Условия задачи и исходные данные
Расстояние между зрачками примерно шесть сантиметров, если человек смотрит прямо вперед и не страдает косоглазием. Расстояние от каждого глаза к поднятому вверх большому пальцу вытянутой руки примерно 60 сантиметров.
Знание этих параметров и оставшихся в памяти сведений из школьного курса геометрии вполне достаточно для определения расстояния до требуемого объекта.
Для определения расстояния до дороги, по которой в это время идет человек, можно воспользоваться двумя способами: по расстоянию между деревьями, которые вдоль дорог высаживают на расстоянии от 3,5 до 5 метров друг от друга, и средней скорости движения человека.
Видео:Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Определение расстояния по деревьям
Чтобы определить расстояние по этому способу, нужно:
- Вытянуть правую руку, пальцы сжать в кулак, большой палец поднять вертикально вверх. Левый глаз закрыть.
- Совместить большой палец с объектом, в данном случае с левым деревом (точка А на чертеже).
- Не двигаясь, открыть левый и закрыть правый глаз. Создается впечатление, что палец переместился в другую точку. Это точка Б на чертеже.
- Оценить расстояние смещения АБ по расстоянию между деревьями на верхнем рисунке. Будем считать, что расстояние между деревьями 3,5 м. Если рассматривать верхний рисунок, где пунктиром обозначены направления взгляда, то надо просто 3,5 м умножить на 10. Расстояние до дороги около 35 метров.
Видео:Определить расстояние от точки С до прямой АВ. Метод прямоугольного треугольника.Скачать

Определение по шагам человека
Для определения расстояния по скорости движения человека начальные действия такие же. Но, закрыв правый и открыв левый глаз, надо считать, сколько шагов пройдет человек, пока его силуэт не совпадет с большим пальцем наблюдателя.
Ширина шага взрослого человека в среднем составляет 75 сантиметров. Умножив количество шагов на 0,75, определяем расстояние АБ на схеме. Расстояние до дороги больше в десять раз.
Подобный метод определения расстояния до какого-то объекта можно использовать в любом случае. Но необходимо иметь какой-то объект для масштабирования смещения.
Опытные туристы знают высоту домов в сельской местности, по которой собираются путешествовать. В среднем высота стен составляет три метра. Высоту дома с крышей определяют по их соотношению: если высота стены и крыши примерно одинакова, то для расчетов расстояния используют высоту дома шесть метров. Если же крыша заметно ниже, можно или отсчитывать расстояние, исходя из высоты стен, или определять примерную высоту дома по пропорциям.
Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Как это работает
Кажущееся смещение объекта относительно неподвижного большого пальца при рассматривании его сначала одним, а потом другим открытым глазом, называется параллаксом.
Параллакс – это угол удаленного объекта между направлениями его обзора с двух концов базовой линии.
В данном примере базовая линия – расстояние между глазами наблюдателя. А все остальное – это элементарная задачка из курса геометрии на подобие треугольников. Известно основание первого треугольника, известна его высота. Известно основание второго подобного треугольника. Надо найти его высоту.
Два глаза у человека, как и у других животных, позволяют мозгу получать объемное изображение и оценивать расстояния.
У птиц глаза расположены по бокам, и их зрение монокулярное (кроме сов и филинов, котрые, как и человек, имеют бинокулярное зрение). Их глаза расположены на «лице» птицы на определенном расстоянии друг от друга, и окружающий мир они видят объемным.
Видео:Определение расстояния от точки до плоскости треугольникаНатуральная величина расстоянияСкачать
Как определить расстояние по звуку и глазомером
| Категория: | Спецподготовка |
|---|
| Опубликовал: solstice, посмотрело: 29 261, фото: 2
В походе, особенно по неизвестной местности и с не очень подробной картой зачастую возникает потребность в ориентировании и определении дальности до каких либо предметов или объектов. И даже GPS-приемник навигатор тут не выручит, так как к нему должна еще прилагаться и карта. А с ними (на территории России) весьма туго. Привязка же координат с туристической карте весьма условная (+- километр).
Возможно, вам помогут простые советы наработанные многолетним туристическим опытом предшественников.
1. На открытой местности населенные пункты видны с 10-12 км.
2. Многоэтажные строения — 8-10 км.
3. Отдельные одноэтажные (частные) дома – 5-6 км.
4. Окна в домах различимы с 4 км.
5. Трубы печей на крышах — 3 км.
6. Отдельные деревья различимы с 2 км.
7. Люди (в виде точек) – 1,5 – 2 км.
8. Движение рук и ног человека — 700 метров.
9. Переплеты оконных рам – 500 метров.
10. Голова человека – 400 м.
11. Цвет и части одежды — 250-300 м.
12. Листья на деревьях – 200 м.
13. Черты лица и кисти рук – 100 м.
14. Глаза в виде точек – 60-80 м.
1. Горящий костер (обычных размеров) виден на расстоянии 6-8 км.
2. Свет электрического фонарика (обычного) – 1,5 – 2 км.
3. Горящая спичка — 1-1,5 км.
4. Огонь сигареты – 400-500 м.
Определение расстояние по звуку сильно зависит от плотности воздуха и в еще большей степени от его влажности. Чем выше давление и выше влажность, тем дальше разносятся звуки. Это необходимо учитывать. Для тихого места и при нормальной влажности:
1. Шум железной дороги (идущего поезда) слышен за 5-10 км.
2. Выстрел из ружья — 2-4 км.
3. Гудок автомобиля, треск пускача трактора, громкий свисток — 2-3 км.
4. Лай собак — 1-2 км.
5. Движение автомобилей по шоссе — 1-2 км.
6. Человеческий крик неразборчиво — 1 – 1,5 км.
7. Звук газующего мотора легкового автомобиля – 0,5 – 1 км.
8. Шум падающего дерева (треск) — 800 – 1000 метров.
9. Стук топора, стук по металлическим предметам — 300-500 метров.
10. Спокойный разговор людей – 200 метров.
11. Негромкая речь, кашель — 50 – 100 метров.
Психологические поправки, которые надо учитывать:
1. Чем дальше предмет, тем он кажется более низким и узким. Поэтому крупные объекты кажутся более близкими (особенно горы), чем есть на самом деле. Лежащие предметы кажутся длиннее, чем стоящие.
2. Расстояние на «гладкой» поверхности (снег, вода, ровное поле) кажется меньше действительного. Ширина реки с пологого берега больше, чем с обрыва.
3. При взгляде снизу вверх склон кажется менее крутым, а расстояние до объектов меньше действительного.
4. Ночь любой свет кажется значительно (!) ближе реального расстояния. Днем светлые предметы так же кажутся более близкими.
5. Обнаженные склоны кажутся более крутыми, чем покрытые растительностью.
6. Обратная дорога кажется более короткой. Ровная дорога кажется короче пересеченной.
Простой способ определения расстояния до предметов методом подобных треугольников.
Этот метод основан на простом математическом соотношении сторон треугольников и знании пары величин, как то: 1) Длина большого пальца человека равна примерно 6 см (60 мм) и 2) Расстояние от большого пальца до глаз человека при вытянутой руке равно примерно 60 см. (Разумеется, вы можете точно измерить свои собственные параметры и внести соответствующие поправки в формулу. Кстати, вместо большого пальца удобнее использовать обычную спичку (длина 45 мм)).
Для того, что бы достаточно точно определить расстояние до объекта, необходимо еще знать его размеры, высоту, в частности.
Например, нам нужно определить расстояние до деревни. Средняя высота стен дома – ок. 3-х метров. Столько же имеет в высоту и крыша. Т.е. высота дома – около 6 метров. Вытягиваем руку, выставив вверх большой палец и оцениваем, в какую часть пальца «укладывается» дом. Допустим, это примерно 1/3 пальца, т.е. 2 см.
В подобных треугольниках истинная высота будет так же соотноситься с истинным расстоянием, как и «проекция» высоты с расстоянием до этой проекции из точки обзора. (или наоборот).
Т.е. 6 метров высоты / Х метров (расстояние) = 2 см/60 см, или
Х метров / 6 = 60/2
Отсюда получаем Что Х = 6 х 30, т.е. до дома 180 метров.
Если знать высоту объекта и иметь при себе линейку (рулетку) то вычислять расстояния можно весьма точно (с достаточной для туристических целей точностью).
Если высота объекта неизвестна даже приблизительно, то предстоит решить немного более сложную задачку, которая позволит вычислить и расстояние до объекта и его высоту. Для этого потребуется сделать два замера проекции высоты объекта с двух разных точек. После первого замера надо приблизиться к объекту на какое то расстояние (и это расстояние запомнить, обозначим его «L», первую проекцию «h1», а вторую «h2»).
Не буду утомлять математическими выкладками, а сразу приведу формулу:
Х = (L x h1) / (h2 – h1) (h2 будет больше, если вы приближались к объекту).
Ну а теперь зная расстояние до объекта несложно вычислить и его высоту (H) :
H (м) = X x h2 / 0.6
Вот такие незамысловатые формулы позволят вам весьма точно ориентироваться на местности и определять расстояния не имея дальномера.
Автор: Константин Тимошенко.
ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ — ПОСТРОЕНИЕМ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ
При определении расстояния до недоступных предметов используют различные приемы, связанные с построением подобных треугольников.
длина рукти/расстояние до столба=величина изображения на линейке/высота столба
Таким образом — до столба 180 м.
Походные эталоны. Для измерений на маршруте с помощью построения подобных треугольников туристам полезно знать некоторые другие походные эталоны.
Длина «четверти», то есть расстояние между концами расставленых большого пальца и мизинца у взрослого человека составляет при-мерно 18—22 см. Длина указательного пальца от основания большого пальца 11—13 см, от основания среднего — 7—8 см. Наибольшее расстояние между концами большого и указательного пальцев 16—18 см, между концами указательного и среднего пальцев — 8—10 см. Расстояние от глаз до поднятого большого пальца вытянутой руки — 60— 70 см. Ширина указательного пальца около 2 см, ширина его ногтя 1 см. Ширина четырех пальцев ладони 7—8 см.
Конкретную длину этих и других эталонов каждый турист определяет самостоятельно и записывает в свою походную записную книжку.
Источники и Дополнительные Ссылки:
© 7517 Русь
© 2009 Славянский Информационный Портал.
Видео:Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

Простые способы измерения расстояний и высот на местности
Видео:Определение расстояния по угловой величинеСкачать

Прямые методы определения линейных расстояний
Точные измерения производятся с помощью мерной рулетки или стальной ленты, длиной 10 или 20 метров. Иногда, применяют длинный шнур (в виде толстого провода), на котором ставятся метки: белые – через каждые 2м и красные – через 10м, с закреплёнными, на концах, шпильками (стальными штырями или деревянными кольями). Важно, чтобы измерительные приспособления не растягивались и были точно отмерены, выверены по эталону.
При обмерах полей и промеров по извилистым контурам, на местности, до сих пор применяют полевой землемерный циркуль-измеритель «Ковылёк» ("двухметровка", старое название – «Сажень»), в виде буквы А. Это раскладывающаяся деревянная вилка, с постоянным раствором ножек, равным 2 метра.
Во время работ по топографической съёмке местности – ведут журнал измерений, составленный по стандартной форме, куда сразу заносятся номера точек стояния и результаты текущих измерений. Дополнительно, составляют, от руки – абрис (схематический чертёж снимаемой, в данный момент, местности).
Приблизительные, грубые измерения с невысокой точностью, производят шагомерно – парами своих шагов (равных, примерно, вашему росту, минус 10-20 сантиметров, в зависимости от темпа ходьбы, степени пересечённости местности и угла наклона земной поверхности). Результаты счёта – последовательно заносятся, записываются в блокнот, в виде таблицы данных для дальнейшего пересчёта пройденных дистанций и отрезков пути, в метры.
Спутниковые навигационные системы (для «гражданских» пользователей)
При измерении больших расстояний, могут помочь GPS-навигаторы (ориентировочная погрешность определения координат точки, при благоприятных условиях работы прибора – ±5–15 метров, в плане, т.е. на горизонтали). Высотомер грубоват – отметки высот определяются с ошибкой от ±10-50м до ±100-150 метров. При использовании смартфонных, мобильных приложений для навигации, погрешность измерений может быть больше, чем у специальных устройств. Максимально возможная точность достижима на многосистемных GPS-Glonass-Beidou приёмниках, при их работе на открытом пространстве, с достаточно ровным рельефом местности, если в это время нет сильных внешних помех, в виде магнитных бурь.
Дистанционные визуальные методы определения расстояний
Дистанционно-визуальные способы измерений длин – они применяются в тех случаях, когда существует непреодолимая преграда, препятствие (река, болото, озеро, глубокий овраг, горное ущелье), но сохраняется прямая видимость, достаточная для производства измерений.
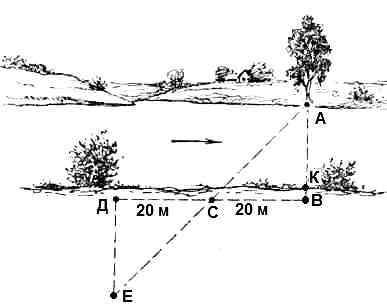
Ширину реки можно определить геометрическим глазомерным способом, путём построения вдоль её берега двух равных прямоугольных треугольников. Выбрав на противоположном берегу (в направлении, перпендикулярном руслу) какой-нибудь заметный предмет «А» (дерево, большой камень и т.п.), расположенный у самой кромки воды, вбивают напротив него колышек «В» (рисунок 1). Вдоль берега, перпендикулярно к линии АВ, отмеряют рулеткой или шагами, например 20м и вбивают колышек «С». На продолжении линии ВС в расстоянии, равном также 20 м, вбивают еще один колышек «Д». От колышка «Д» в направлении ДЕ, перпендикулярном (направления задаются при разведении рук в стороны и сведении их ладонями, прямо перед собой или с помощью крестообразного эккера) к линии ДВ, надо идти от реки до тех пор, пока колышек «С» не окажется на одной линии с предметом «А». Так как треугольники ABC и ЕДС абсолютно и полностью равны, то ширина реки будет равна расстоянию ДЕ минус ВК (интервал до уреза воды). Если плечи ДС и СВ не равны (нет возможности пройти вдоль берега; мешают густые заросли), то AB = DE*BC/CD
Рис.1
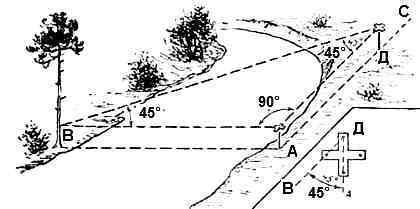
Определить ширину реки можно и не отходя от воды, построением на местности прямоугольного равнобедренного треугольника АДВ (рис. 2). Построив на точке «А» прямой угол, отходят в направлении АС до такой точки «Д», из которой предмет «В» будет засекаться под углом 45° (в этом случае, АВ=АД). Для разбивки углов применяется самодельный крестообразный эккер (в виде квадратного листа бумаги с загнутыми, кверху, уголками или, установленной на подставку, плоской деревянной крестовины с четырьмя вбитыми, по квадрату, шпильками), с помощью которого строят углы 45° и 90° от ходовой линии (основной магистрали). На точке «А», для лучшей её видимости при расстановке вешек в створе, ставится хорошо заметный «макет» (например, крепится белый лист бумаги, обращённый в сторону пункта «Д»).
Экспресс-метод, без установки эккера на штативе – две перекрещенных прямых веточки, одинаковой длины, держать горизонтально на уровне глаз так, чтобы одна ветка была параллельна течению реки и направлена на точку «А» (смотреть, прикрыв один глаз). Тогда, линия угла-сорокапятки, проходящая через концы веточек – смотрится-визируется закрыв другой глаз и слегка наклонив голову. Можно визировать и с помощью шкалы компаса, или оптического приспособления буссоли, или циферблата наручных часов (в качестве направляющей можно использовать измерительную линейку, прикладывая её ребром через центр лимба).
Имея возможность провести на местности триангуляцию (померить угломером или по лимбу компаса) и посчитать тангенс угла (в полевых условиях, это возможно проделать без калькулятора и точных математических таблиц Брадиса, при помощи транспортира, линейки и циркуля), можно визировать под любым углом, а затем – считать по формуле:
АВ = АД * tg АДВ .
Если угол равен 45 градусов, тогда tg(45°)=1 и, соответственно, АВ=АД
tg(64°) = 2 и АВ=АД*2
tg(72°) = 3 и АВ=АД*3
Рис.2
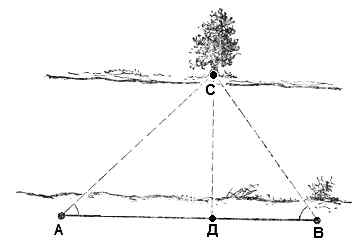
Достаточно точно ширина реки может быть установлена способом прямой засечки (рис. 3). Для этого на противоположном берегу выбирают приметный предмет «С», а вдоль берега, на котором находится исследователь, прокладывают базис АВ и измеряют длину его. Из точек «А» и «В» делают засечки на точку «С», т. е. измеряют углы CAB и ABC. Построив с помощью мерной линейки и транспортира треугольник ABC, можно получить в принятом для базиса АВ масштабе искомую ширину реки.
Тем же способом ширина реки может быть определена и без непосредственного измерения углов CAB и ABC, с помощью графических засечек на планшете. Надо отложить на бумаге длину базиса AB в выбранном масштабе, затем из концов базиса, ориентировав, стоя на угловых точках, планшетку, прочертить направления на какой-нибудь видимый предмет «С» противоположного берега. Тогда, ширину реки можно определить графически – на чертеже, пересчитав по его масштабу.
Рис.3
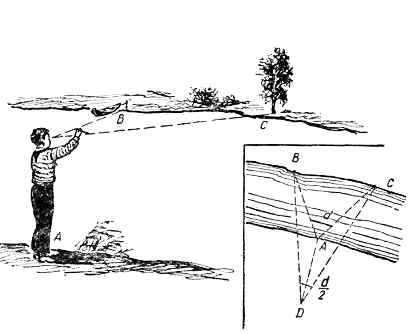
Весьма прост и удобен приближенный прием измерения ширины реки (или расстояния до недоступного объекта) при помощи травинки или нитки. Стоя на берегу реки в точке «А», замечают на противоположном ее берегу два приметных предмета (например лодку В и дерево «С»), расположенных близ уреза (рис. 4). Затем, взяв травинку (нитку) за ее концы вытянутыми перед собой руками, замечают ее длину «d», которой закрывается промежуток ВС между выбранными предметами (смотреть надо одним глазом). Затем, сложив травинку пополам, отходят от реки до тех пор (точка «D»), пока промежуток ВС не будет закрыт травинкой. Пройденное расстояние AD будет равно ширине реки.
Рис.4
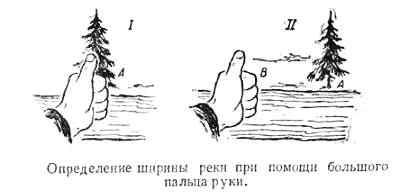
Существует и такой, самый быстрый, но весьма приближённый способ определения ширины реки – закрывают правый глаз и направляют поднятый вверх большой палец вытянутой горизонтально руки (рис. 5) в направлении приметного предмета «А» противоположного берега. Затем, поменяв открытый глаз (так появляется стереоскопический эффект в виде стереопары изображений из двух различных точек наблюдения), замечают, что палец как бы отскочил вбок от наблюдаемого предмета в точку «В». Оценив на глаз расстояние АВ, в метрах (предполагая, примерно, высоту или ширину предметов), и умножив его на 10, получают примерную ширину реки. Человек при таких измерениях – выступает как стереофотограмметрический прибор.
Рис.5
Видео:Метод большого пальцаСкачать

Определение расстояний по угловой величине известных предметов
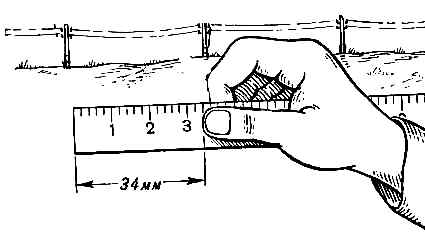
Пример (рис. 6). Расстояние между телеграфными столбами линии связи, равное 55м (у старых, деревянных, обычно — 50-60 метров интервала, с высотой 6м от земли), покрывается 34 миллиметровыми делениями линейки (3.4см), удаленной от глаз на 50 сантиметров (рука вытянута прямо перед собой). Тогда, расстояние до телеграфной линии, по уравнению соотношения сторон подобных треугольников, равно:
Д = 55м * ( 50см / 3.4см ) = 809 м.
Если столбы видны не под прямым углом, а сбоку, тогда, чтобы исключить завышение расстояния до них – надо результат счёта умножить ещё и на поправочный коэффициент:
для 45 градусов – 0.7
30° – 0.9
Например, для рассмотренного примера, при расположении линии столбов под углом 45 градусов относительно наблюдателя – реальное расстояние будет:
809 * 0.7 = 566 метров (между 2-мя измеренными столбами). При больших углах – расст-е определяется по высоте опор.
Стандартное расстояние между опорами электросети высокого напряжения (ЛЭП) – 100 метров. Высота заводских труб – 30 м
Если нет линейки, то для измерений можно использовать подручные средства, например – спичечный коробок (5 сантиметров – максимум, 2.5см – до середины).
Точность определения дистанции по угловым величинам составляет 5-10% длины измеряемого расстояния.
Рис.6
Видео:Определить расстояние от точки до плоскости (от точки D до плоскости треугольника ABC)Скачать
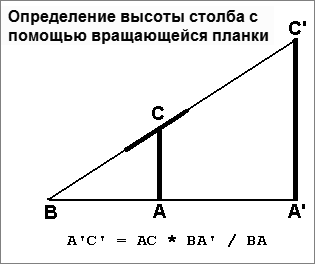
Определение высоты столба с помощью вращающейся планки
Нужно поставить на некотором расстоянии от столба А’С’ шест АС с вращающейся планкой и направить планку на верхнюю точку С’ столба (рис.7). С противоположной стороны, прицелившись по рейке – отметить на поверхности земли точку В.
Из подобия треугольников А’С’В и АСВ следует:
A’C’ = AC * BA’ / BA
то есть, чтобы определить высоту А’С’ столба, дастаточно будет знать высоту АС шеста и длину двух отрезков ВА’ и ВА
Можно померить и без дополнительных приспособлений. Один человек, лёжа на земле, смотрит на вершину объекта – по макушке головы стоящего помощника. Рост известен, горизонтальные расстояния – промеряются шагомерно. Данный способ применялся ещё во времена СССР, при проведении военно-патриотических и спортивных игр среди молодёжи (учащихся средних и старших классов общеобразовательных школ), с элементами военных учений, при участии кадровых офицеров вооруженных сил. У советских пионеров эти спортивно-массовые мероприятия назывались «Зарница», у старшеклассников – «Орлёнок». У зарубежных бой-скаутов, наверно, тоже могло быть что-то похожее.
Рис.7
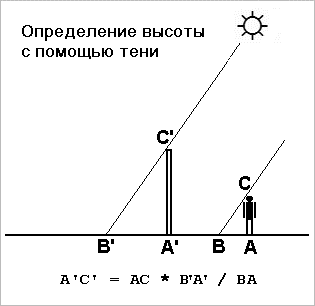
Определение высоты дерева с помощью тени
В солнечную погоду, измерить длину тени от дерева и от человека. Используя подобие треугольников, составить численную пропорцию (схема и формула показаны на рисунке 8) или построить графически, в выбранном масштабе.
В пасмурный день, когда не видно солнца на небе и лунной ночью, поставленная задача решается другими методами. Например, можно определить высоту с помощью способа, изображённого на рисунке 2 (построение прямоугольного равнобедренного треугольника), используя, дополнительно, современную лазерную указку, ориентированную по эккеру на 45° относительно земной поверхности – для визирования вершины предмета. Эккерная рамка ставится в вертикальной плоскости, а прямой угол между поверхностью земли и стороной квадрата крестовины — выставляется по отвесу.
Если произвольный угол A’B’C’ мерить при помощи угломера, тогда придётся смотреть в таблицах тангенсы угла и считать.
Рис.8
Определение высоты дерева с помощью зеркала
Если имеется зеркало, расположенное на земле горизонтально или лужа с дождевой водой, можно использовать оптическое свойство – равенство углов падения и зеркального отражения светового луча. Для этого, нужно встать на точке, из которой, в середине зеркала видна вершина предмета. Зная свой рост (на уровне глаз), расстояние до центра зеркала и от него до предмета, используя подобие треугольников, составить численную пропорцию (как на рисунке 8) или построить схему графически, в выбранном масштабе.
Определение крутизны скатов
С помощью отвеса (нить с небольшим грузиком) и транспортира (обычного измерителя или офицерской линейки). Становятся сбоку ската. Определяют, по шкале, угол между штрихом 90°, на транспортире, и вертикальной нитью.
Горизонтальным визированием и промером шагами, при крутизне подъёма до 20-25°. Располагаясь внизу ската, в точке А, визируют, горизонтально, на уровне глаз, выше по склону холма, точку В. Затем, парами шагов, промеряют расстояние АВ. Крутизна ската, при углах до 20-25°, определяется по формуле:
где А – крутизна ската, градусов; n – количество пар шагов. Точность определения – до 2-3°
Горизонтальным визированием, точным промером расстояния до намеченной точки (расположенной выше по склону горы), расчётом по формуле (катет треугольника – равен высоте до уровня глаз, гипотенуза – расстоянию) для синуса угла, и нахождением соответствующего числа по таблице.
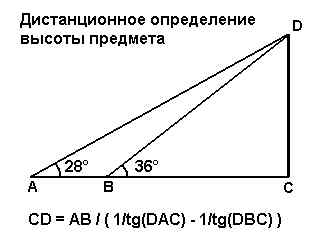
Дистанционное определение высоты предмета
Например, нужно определить высоту предмета (рис. 9), не подходя к нему (невозможно преодолеть препятствия в виде реки или глубокого оврага). Измеряются углы в точках А (DАС) и В (DВС), а так же расстояние АВ между ними. В примере на картинке:
DАС = 28°
DВС = 36°
АВ = 15 метров
тогда, высота предмета:
CD = АВ / ( 1/tg(DАС) – 1/tg(DВС) ) =
= 15 / ( 1/tg(28°) – 1/tg(36°) ) =
= 15 / ( 1/0.53 – 1/0.73 ) =
= 15 / ( 1.89 – 1.38 ) =
= 15 / 0.51 = 29 метров, с общей суммарной ошибкой измерений – до 10-20%
Рис.9
Примеры, разобранные на этой Интернет-странице, можно бесплатно скачать, сохранить на жёсткий диск своего компьютера или распечатать на принтере, чтобы удобнее было осваивать практические методы измерения расстояний и эффективнее тренироваться в реальных, полевых условиях. Правильное и точное определение ширины реки или водоёма – обязательно необходимо проводить перед форсированием водной преграды. В войсковых подразделениях, этим занимаются специалисты инженерной разведки.
Видео:Расстояние от точки до плоскостиСкачать
Высокоточные измерения расстояний
При наличии дальномера (лазерные, свето- и радиодальномеры), получается довольно высокая точность, которая требуется при проведении геодезических работ, где эти приборы и применяют профессионалы. Туристам, в их походах и путешествиях, такие миллиметровые погрешности не нужны.
ПРИЛОЖЕНИЯ
Таблица синусов, косинусов, тангенсов и котангенсов углов от 0° до 90°
Точность вычислений – до третьего знака после запятой. Расчёт был проведён в электронных таблицах Excel по формулам, вида:
TAN(A1*pi()/180)
Пример: tg(60°) = 1.732
| a | sin a | cos a | tg a | ctg a |
|---|---|---|---|---|
| 0 | 0,000 | 1,000 | 0,000 | |
| 1 | 0,017 | 1,000 | 0,017 | |
| 2 | 0,035 | 0,999 | 0,035 | |
| 3 | 0,052 | 0,999 | 0,052 | |
| 4 | 0,070 | 0,998 | 0,070 | |
| 5 | 0,087 | 0,996 | 0,087 | |
| 6 | 0,105 | 0,995 | 0,105 | |
| 7 | 0,122 | 0,993 | 0,123 | |
| 8 | 0,139 | 0,990 | 0,141 | |
| 9 | 0,156 | 0,988 | 0,158 | |
| 10 | 0,174 | 0,985 | 0,176 | 5,671 |
| 11 | 0,191 | 0,982 | 0,194 | 5,145 |
| 12 | 0,208 | 0,978 | 0,213 | 4,705 |
| 13 | 0,225 | 0,974 | 0,231 | 4,331 |
| 14 | 0,242 | 0,970 | 0,249 | 4,011 |
| 15 | 0,259 | 0,966 | 0,268 | 3,732 |
| 16 | 0,276 | 0,961 | 0,287 | 3,487 |
| 17 | 0,292 | 0,956 | 0,306 | 3,271 |
| 18 | 0,309 | 0,951 | 0,325 | 3,078 |
| 19 | 0,326 | 0,946 | 0,344 | 2,904 |
| 20 | 0,342 | 0,940 | 0,364 | 2,747 |
| 21 | 0,358 | 0,934 | 0,384 | 2,605 |
| 22 | 0,375 | 0,927 | 0,404 | 2,475 |
| 23 | 0,391 | 0,921 | 0,424 | 2,356 |
| 24 | 0,407 | 0,914 | 0,445 | 2,246 |
| 25 | 0,423 | 0,906 | 0,466 | 2,145 |
| 26 | 0,438 | 0,899 | 0,488 | 2,050 |
| 27 | 0,454 | 0,891 | 0,510 | 1,963 |
| 28 | 0,469 | 0,883 | 0,532 | 1,881 |
| 29 | 0,485 | 0,875 | 0,554 | 1,804 |
| 30 | 0,500 | 0,866 | 0,577 | 1,732 |
| 31 | 0,515 | 0,857 | 0,601 | 1,664 |
| 32 | 0,530 | 0,848 | 0,625 | 1,600 |
| 33 | 0,545 | 0,839 | 0,649 | 1,540 |
| 34 | 0,559 | 0,829 | 0,675 | 1,483 |
| 35 | 0,574 | 0,819 | 0,700 | 1,428 |
| 36 | 0,588 | 0,809 | 0,727 | 1,376 |
| 37 | 0,602 | 0,799 | 0,754 | 1,327 |
| 38 | 0,616 | 0,788 | 0,781 | 1,280 |
| 39 | 0,629 | 0,777 | 0,810 | 1,235 |
| 40 | 0,643 | 0,766 | 0,839 | 1,192 |
| 41 | 0,656 | 0,755 | 0,869 | 1,150 |
| 42 | 0,669 | 0,743 | 0,900 | 1,111 |
| 43 | 0,682 | 0,731 | 0,933 | 1,072 |
| 44 | 0,695 | 0,719 | 0,966 | 1,036 |
| 45 | 0,707 | 0,707 | 1,000 | 1,000 |
| 46 | 0,719 | 0,695 | 1,036 | 0,966 |
| 47 | 0,731 | 0,682 | 1,072 | 0,933 |
| 48 | 0,743 | 0,669 | 1,111 | 0,900 |
| 49 | 0,755 | 0,656 | 1,150 | 0,869 |
| 50 | 0,766 | 0,643 | 1,192 | 0,839 |
| 51 | 0,777 | 0,629 | 1,235 | 0,810 |
| 52 | 0,788 | 0,616 | 1,280 | 0,781 |
| 53 | 0,799 | 0,602 | 1,327 | 0,754 |
| 54 | 0,809 | 0,588 | 1,376 | 0,727 |
| 55 | 0,819 | 0,574 | 1,428 | 0,700 |
| 56 | 0,829 | 0,559 | 1,483 | 0,675 |
| 57 | 0,839 | 0,545 | 1,540 | 0,649 |
| 58 | 0,848 | 0,530 | 1,600 | 0,625 |
| 59 | 0,857 | 0,515 | 1,664 | 0,601 |
| 60 | 0,866 | 0,500 | 1,732 | 0,577 |
| 61 | 0,875 | 0,485 | 1,804 | 0,554 |
| 62 | 0,883 | 0,469 | 1,881 | 0,532 |
| 63 | 0,891 | 0,454 | 1,963 | 0,510 |
| 64 | 0,899 | 0,438 | 2,050 | 0,488 |
| 65 | 0,906 | 0,423 | 2,145 | 0,466 |
| 66 | 0,914 | 0,407 | 2,246 | 0,445 |
| 67 | 0,921 | 0,391 | 2,356 | 0,424 |
| 68 | 0,927 | 0,375 | 2,475 | 0,404 |
| 69 | 0,934 | 0,358 | 2,605 | 0,384 |
| 70 | 0,940 | 0,342 | 2,747 | 0,364 |
| 71 | 0,946 | 0,326 | 2,904 | 0,344 |
| 72 | 0,951 | 0,309 | 3,078 | 0,325 |
| 73 | 0,956 | 0,292 | 3,271 | 0,306 |
| 74 | 0,961 | 0,276 | 3,487 | 0,287 |
| 75 | 0,966 | 0,259 | 3,732 | 0,268 |
| 76 | 0,970 | 0,242 | 4,011 | 0,249 |
| 77 | 0,974 | 0,225 | 4,331 | 0,231 |
| 78 | 0,978 | 0,208 | 4,705 | 0,213 |
| 79 | 0,982 | 0,191 | 5,145 | 0,194 |
| 80 | 0,985 | 0,174 | 5,671 | 0,176 |
| 81 | 0,988 | 0,156 | 0,158 | |
| 82 | 0,990 | 0,139 | 0,141 | |
| 83 | 0,993 | 0,122 | 0,123 | |
| 84 | 0,995 | 0,105 | 0,105 | |
| 85 | 0,996 | 0,087 | 0,087 | |
| 86 | 0,998 | 0,070 | 0,070 | |
| 87 | 0,999 | 0,052 | 0,052 | |
| 88 | 0,999 | 0,035 | 0,035 | |
| 89 | 1,000 | 0,017 | 0,017 | |
| 90 | 1,000 | 0,000 | 0,000 |
При отсутствии таблиц Брадиса, инженерного калькулятора и компьютера, значения тригонометрических функций можно посчитать, с произвольно высокой точностью, и на простейшем арифмометре, с помощью арифметических операций сложения, вычитания, умножения и деления по формулам рядов:
sin x = x – x^3/1*2*3 + x^5/1*2*3*4*5 – x^7/1*2*3*4*5*6*7 + x^9/1*2*3*4*5*6*7*8*9 -.
cos x = 1 – x^2/1*2 + x^4/1*2*3*4 – x^6/1*2*3*4*5*6 + x^8/1*2*3*4*5*6*7*8 -.
tg x = x + (1/3 * x^3) + (2/15 * x^5) + (17/315 * x^7) + .
В степень – число возводится с помощью многократного перемножения.
Например, аргумент в кубе: x^3 = x*x*x На калькуляторе, после набора числа, последовательно нажимаются кнопки: * = =
Главные формулы из геометрии, использовавшиеся в разобранных примерах
Теорема Пифагора: a^2 + b^2 = c^2
В прямоугольном треугольнике ABC (рис.10) – отношение двух его сторон, например катета a к гиптенузе c, зависит от величины одного из острых углов, например A.
Основные тригонометрические функции для прямоугольного треугольника:
Синус: sin A = a / c (отношение противолежащего катета к гипотенузе)
Косинус: cos A = b / c
Тангенс: tg A = a / b
Котангенс: ctg A = b / a
A + B = 90°
B = 90° – A
a = c * sin A = c * cos B
a = b * tg A
Рис.10 Основные тригонометрические формулы для прямоугольного треугольника.
Если на карте отсутствует масштабная линейка и не указан численный масштаб
На топокарте, по вертикали (на линии север-юг) в 1 минуте, приблизительно – 1.85 километров (мало зависимо от географической широты на земном глобусе). И если имеется подписанная градусная сетка, то по ней, графически, турист может определить, сколько в одном сантиметре, для измерения расстояний в любых направлениях на карте. Когда указаны не минуты, а доли градуса, то соотношение:
0.1 градуса = 11.1 км
0.01 градуса = 1.11 км
// Международная морская миля (действует с 1929 года), применяемая в географии и в навигации, для определения расстояний, равна 1852 метра, что, примерно, соответствует одной минуте дуги земного меридиана на сороковых широтах. Это удобно для навигационных расчетов, при решении прикладных задач. В судоходстве, в качестве основной единицы скорости движения, применяется УЗЕЛ (от англ. knot «узел»; 1 kn равен 1 пройденной морской миле, за час движения). Международный КАБЕЛЬТОВ (единица длины, для измерения, в мореходной практике, сравнительно небольших расстояний, равен 1/10 морской мили.
Список использованной литературы и ссылки на Интернет-ресурсы
Андреев Н.В. Топография и картография: Факультативный курс. М., Просвещение, 1985
https:// school-kraevedenie.narod.ru/ antimonov/ – Школьные походы по изучению рек, озер и болот родного края. Москва, 1963 г.
Краткий справочник. Издание военно-инженерной Академии Красной Армии имени В.В.Куйбышева, 1941 год.
www.festival.1september.ru/ articles/418615/ – Измерительные работы на местности в курсе геометрии основной школы.
www.kakras.ru/mobile/tourism-compass-and-map.html – Карта и компас (дирекционный угол, движение по азимутам и примеры расчётов).
Контроль выбросов в атмосферу на сайте ООО «Лабораторно-исследовательский Центр».
Окружность можно нарисовать на листе бумаги – с помощью нитки и воткнутой булавки. Туристические минисправочники. Прикладная топография.
🌟 Видео
Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Определить расстояние от вершины S до плоскости основания ABCСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

расстояние от точки до плоскостиСкачать

Расстояние от точки до плоскости. Метод замены плоскостей проекцийСкачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

11. Определение расстояния от точки до плоскости методом замены плоскостей проекцийСкачать

9 класс. Определение расстояний в астрономии методом параллаксаСкачать

Построение натуральной величины треугольника методом вращенияСкачать