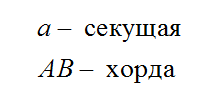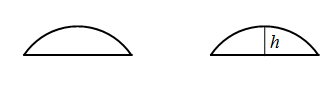Определение окружности определения диаметра хорды секущей касательной (2 видео)

Определение окружности определения диаметра хорды секущей касательной

Окружность — геометрическое место точек плоскости, равноудаленных от одной ее точки (центра).

Равные отрезки, соединяющие центр с точками окружности, называются радиусами.

Круг — часть плоскости, лежащая внутри окружности.

Содержание

Хорда, дуга, диаметр
Касательная к окружности
Определение сегмента, сектора*
Хорда, секущая, касательная
Определения
Свойства
Окружность и круг
теория по математике 📈 планиметрия
Определения
Свойство хорд
Длина окружности
Дуга, касательная, круг, сектор, сегмент
Свойства касательной
📹 Видео

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Хорда, дуга, диаметр

Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности, — хордой. Хорда, проходящая через центр О, называется диаметром. Диаметр равен двум радиусам.

Часть окружности называется дугой.

Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.

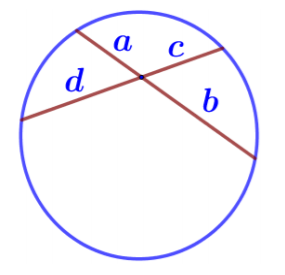
Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Касательная к окружности

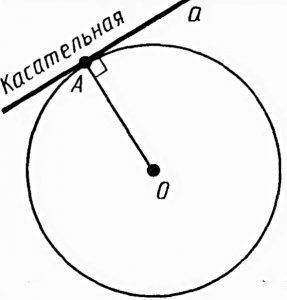
Касательная — прямая, имеющая с окружностью только одну общую точку.

Теорема. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Обратная теорема (признак касательной). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение сегмента, сектора*

Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Перпендикуляр, проведенный из середины хорды до пересечения с дугой называется стрелкой дуги. Длина стрелки называется высотой сегмента.

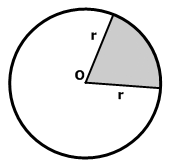
Сектором называется часть круга, ограниченная дугой и двумя радиусами, проведенными к концам дуги.

Сектор, отсекаемый радиусами, образующими угол 90 0 , называется квадрантом.

Видео:Окружность / Касательная, хорда, секущая / задача из ЕГЭ #27862Скачать

Хорда, секущая, касательная

Видео:Окружность, касательная, секущая и хорда | МатематикаСкачать

Определения

Хорда – отрезок, соединяющий две точки окружности.

В частности, хорда, проходящая через центр окружности, называется диаметром .

Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Свойства

Радиус, проведенный в точку касания, перпендикулярен касательной

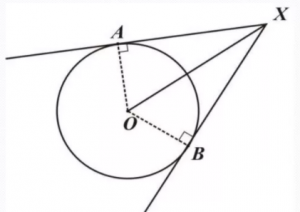
Отрезки касательных, проведенных к окружности из одной точки, равны.

Отрезки пересекающихся хорд связаны соотношением:

Произведения отрезков секущих, проведенных из одной точки, равны:

Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки:

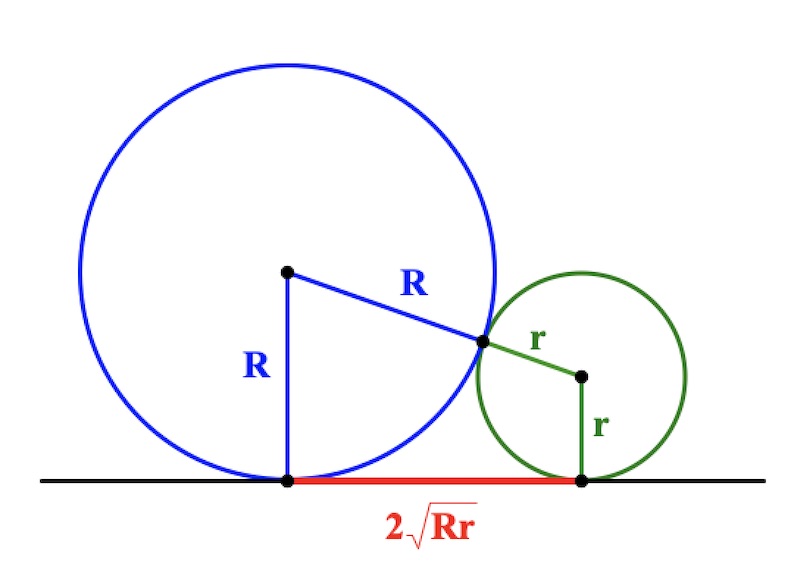
Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов Видеодоказательство

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Окружность / Касательная, хорда, секущая / задача из ЕГЭ #27858Скачать

Окружность и круг

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

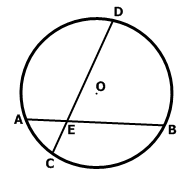
На рисунке центр окружности обозначен точкой О. 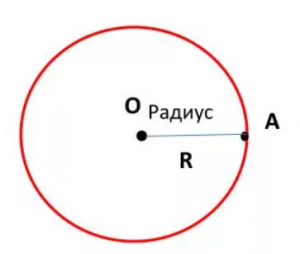Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.

Свойство хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Видео:Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Дуга, касательная, круг, сектор, сегмент

Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

Свойства касательной

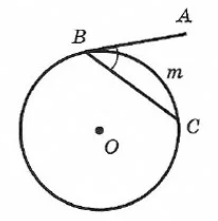
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

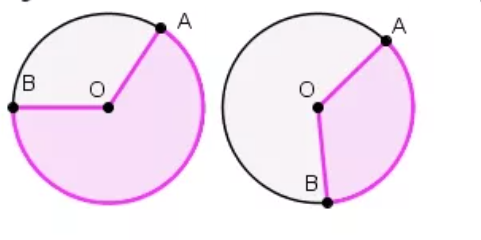
Сектор и его площадь

Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.