Описанная около треугольника окружность на клетчатой бумаге (7 видео)

Описанная около треугольника окружность на клетчатой бумаге

Содержание

Источник задания: Решение 4538. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.
Круг на клетчатой бумаге
Решение №1250 На клетчатой бумаге с размером клетки 1х1 изображён равносторонний треугольник.
📹 Видео

Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Источник задания: Решение 4538. ЕГЭ 2016 Математика, И.В. Ященко. 30 вариантов. Ответ.

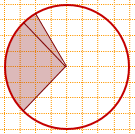
Задание 3. Найдите радиус окружности, описанной около треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в сантиметрах.

Центр радиуса описанной окружности лежит в точке пересечения серединных перпендикуляров всех сторон треугольника. Радиус описанной вокруг треугольника окружности можно найти по формуле

где — длины сторон треугольника; — его площадь.

Из рисунка видно, что основание треугольника равно 4 см, его высота также равна 4 см и треугольник равнобедренный. Найдем длину его боковой стороны из теоремы Пифагора:

Площадь треугольника определяется как произведение половины его высоты на основание:

Таким образом, радиус описанной окружности равен

см.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Круг на клетчатой бумаге

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Так как центральный угол, соответствующий данному сектору, равен 90º, то

2) На клетчатой бумаге изображён круг.

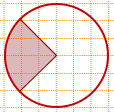
Какова площадь круга, если площадь заштрихованного сектора равна 17?

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

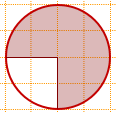
Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

5) На клетчатой бумаге изображен круг площадью 96.

Найдите площадь заштрихованного сектора.

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

Рассмотрим треугольник ABC.

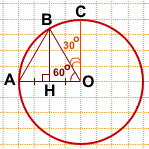
Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

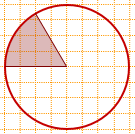
Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

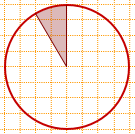
Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

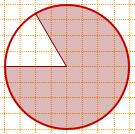
Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) Центральный угол равен 30+45=75°,

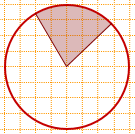
площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

10) Центральный угол равен 180-30=150°,

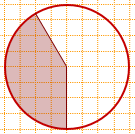
площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

11) Центральный угол равен 60-45=15°,

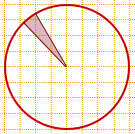
площадь заштрихованного сектора составляет 1/24 площади круга

12) Центральный угол равен 15+90=105°

Видео:Найдите радиус окружности, описанной около треугольника, изображённого на клетчатой бумагеСкачать

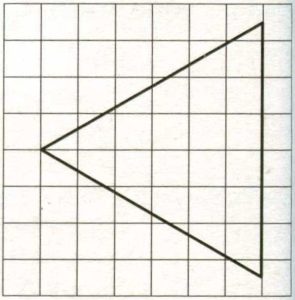
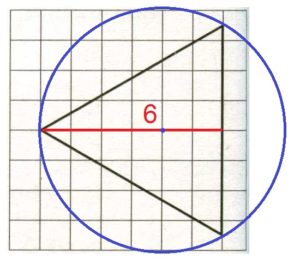
Решение №1250 На клетчатой бумаге с размером клетки 1х1 изображён равносторонний треугольник.

На клетчатой бумаге с размером клетки 1х1 изображён равносторонний треугольник. Найдите радиус описанной около него окружности.

Источник: ЕГЭ 2021 Ященко (36 вар)

Радиус окружности, описанной около равностороннего треугольника, равен frac его высоты.
Высота этого треугольника равна 6 . Радиус окружности равен:

fraccdot 6=2cdot 2=4

Ответ: 4.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.7 / 5. Количество оценок: 7

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.