Окружности радиусов 45 и 55 касаются внешним

Задание № 26 из сборника ОГЭ 10 вариантов Ященко И.В.

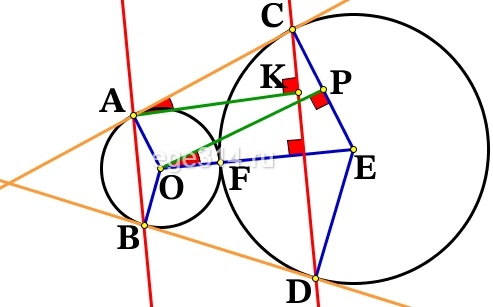
Окружности радиусов 45 и 55 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и К – на второй. При этом АС и ВК – общие касательные окружностей. Найдите расстояние между прямыми АВ и СК.

Касательная перпендикулярна радиусу, проведённому в точку касания. В прямоугольной трапеции ВКОМ: ВМ=45, МО=45+55=100, КО=55, МНКО, НО=55-45=10, cosМОН=0,1.

В прямоугольном треугольнике ЕОК: cosЕОК=0,1=ОЕ:ОК => ОЕ=5,5.

Треугольник ВМР подобен КОЕ (равны соответственные углы при параллельных прямых) с коэффициентом подобия = 911, значит РМ = 4,5.

Расстояние между прямыми АВ и СК соответствует длине отрезка РЕ = МО-ОЕ+МР=100 – 5,5 + 4,5 = 99.

1) Окружности радиусов 15 и 21 касаются внешним образом. Точки А и В лежат на первой окружности, точки C и D — на второй. При этом АС и ВD- общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.(Ответ 35)

2) Окружности радиусов 36 и 45 касаются внешним образом. Точки А и В лежат на первой окружности, точки C и D — на второй. При этом АС и ВD- общие касательные окружностей. Найдите расстояние между прямыми АВ и СD. (Ответ 80)

3) Окружности радиусов 12 и 52 касаются внешним образом. Точки А и В лежат на первой окружности, точки C и D — на второй. При этом АС и ВD- общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Расстояние между прямыми AB и CD – это FK. FK= NO+ FN-KO.

1) Рассмотрим MAB. Он равнобедренный, так как МА=МВ – касательные, проведённые к окружности из одной точки. Аналогично MCD – равнобедренный.

2) Рассмотрим MAN и MCD. Они прямоугольные, так как NА MA и ОС МС, являются радиусами и касательными. У данных треугольников угол при вершине М – общий, а углы при вершинах А и С — прямые. Данные треугольники подобны по двум углам. Составим пропорцию:

СОАN = МОМN. N0 = сумме двух радиусов. N0=12+52=64. Обозначим MN=х, тогда получим 5212 = 64+хх. Решаем уравнение х=19,2. Значит МN=19,2.

3) АF в прямоугольном МАN, является высотой, проведённой из прямого угла А. Тогда МАN подобен АFN. У подобных треугольников углы равны. FАN=АМN. Значит равны их синусы.

Синус = отношение противолежащего катета к гипотенузе. АN:МN=FN:АN. (*)

4) АFN подобен СКО из равенства соответственных углов при параллельных прямых. Составим пропорцию: АN:СО=FN:КО или FN: АN=КО:СО. Используя (*), получим равенство:

АN:МN=FN:АN=КО:СО. Или 12:19,2= FN:12=КО:52. Следовательно FN=7,5, КО=32,5.

5) Найдём FK= NO+ FN-KO, FК=64+7,5-32,5=39.

В АВС на его медиане ВМ отмечена точка К так, что ВК:КМ = 10 : 9. Прямая АК пересекает сторону ВС в точке Р. Найдите отношение площади четырёхугольника КРСМ к площади АВС.

Треугольники АКМ и СКМ – равновеликие, так как КМ является медианой. Обозначим площадь АКМ= х. Рассмотрим отношение площадей АВК и АМК: высоты, проведённые из вершины А у них равны. Площадь АВК=0,5·АН·ВК, площадь АМК=0,5·АН·МК, где АН – высота, проведённая из вершины А к прямой содержащей стороны ВК и МК. Тогда SАВК : SАМК=0,5·АН·ВК0,5·АН·МК = 109. Или SАВК = 109х.

Рассмотрим отношение площадей АВК и РВК: высоты, проведённые из вершины В у них равны. Площадь АВК=0,5·АК·ВЕ, площадь РВК=0,5·ВЕ·РК, где ВЕ – высота, проведённая из вершины В к прямой содержащей стороны АК и РК. Тогда SАВК : SВРК=0,5·АК·ВЕ0,5·ВЕ·РК = АКРК.

Рассмотрим отношение площадей АКС и СРК: высоты, проведённые из вершины С у них равны. Площадь СРК=0,5·РК·СО, площадь АКС=0,5·АК·СО, где СО – высота, проведённая из вершины С к прямой содержащей стороны АК и РК. Тогда SАКС : SСРК=0,5·АК·СО0,5·СО·РК = АКРК.

Значит SАВК : SВРК = SАКС : SСРК, SАКС = 2·SАКМ = 2х. Получаем 109х : SВРК = 2х : SСРК или

SВРК = 59 SСРК. Пусть SСРК = у, тогда SВРК = 59у.

Треугольники АВМ и СВМ – равновеликие, так как ВМ является медианой. Площадь АВМ равна сумме площадей АВК и АКМ. SАВМ = 109х + х = 199 х.

Площадь СВМ равна сумме площадей РВК, СКР и СКМ. SСВМ = 59у + у + х = 149 у + х.

SАВМ = SСВМ, тогда 199 х = 149 у + х, или 109 х = 149 у. у = 57 х.

SКРСМ = SСРК + SСМК = 57 х + х = 127 х, SАВС = 2·SАВМ =2· 199 х = 389 х.

Получаем, SКРСМ : SАВС = 127 х : 389 х = 54:133.

Аналогичная задача В треугольнике АВС на его медиане ВМ отмечена точка К так, что ВК:КМ=7:3. Прямая АК пересекает сторону ВС в точке Р. Найдите отношение площади треугольника ВКР к площади четырехугольника КРСМ.

Пусть площадь треугольника . Выразим площади треугольника и четырехугольника через . Для решения задачи нам понадобится следующий факт: Пусть дан треугольник АВС и точка М на стороне АС, которая делит сторону АС в отношении . Тогда

1. — так как ВМ — медиана, следовательно, точка М — середина АС и АМ=МС.

2. , так как по условию ВК:КМ=7:3. Следовательно,

3. Найдем, в каком отношении делит точка Р отрезок ВС. Для этого через точку Р проведем прямую BD параллельно АС.

Рассмотрим треугольники и . Треугольник подобен треугольнику по двум. . Пусть . Тогда

Теперь рассмотрим подобные треугольники и (они также подобны по двум углам).

Ответ:

Середина диагонали АС выпуклого четырёхугольника АВСD удалена от каждой из его сторон на расстояние, равное 12. Найти площадь четырёхугольника, если ВD = 26.

Треугольники ALO, AKO, CMO, CHO равны как прямоугольные треугольники по катету и гипотенузе (АО=ОС – О – середина АС, LO=КО=ОН=ОМ по условию). Значит 1 = 2 = 3 = 4 (рис.1). АС является диагональю и биссектрисой. В треугольниках АВС и АDC углы при основаниях равны, следовательно они равнобедренные и они равны между собой по стороне (общая) и прилежащим углам. Четырёхугольник АВСD – ромб. Диагонали ромба перпендикулярны, и точкой пересечения делятся пополам. ОD=ОВ=26:2=13.

В ОDН: DH= 5, tg ODH=12/5.

В ODC: tg ODC = OC/OD=12/5 => OC=13·12:5=31,2.

Найдем площадь ромба через полу произведение диагоналей. S=AC·BD:2= 26·62,4:2 = 811,2.

Аналогичная задача. Середина диагонали ВD выпуклого четырёхугольника АВСD удалена от каждой из его сторон на расстояние, равное 7. Найти площадь четырёхугольника, если АC = 50. (Ответ:4375/12)

Точка О является основанием высоты, проведённой из вершины тупого угла А треугольника АВС к стороне ВС. Окружность с центром в точке О и радиусом ОА пересекает прямые АВ и АС в точках Р и М, отличных от А, соответственно. Найдите АС, если АВ =9, АР = 8, АМ = 6.

Обозначим радиус окружности через х, тогда МО=ОА=ОР=х.

В АОВ: cos ОАВ = ОА : АВ= х : 9.

В АОР: cos ОАР = cos ОАВ=х : 9, по теореме косинусов ОР = ОА+ АР — 2·ОА·АР· cos ОАР или

х = х + 8 — 2·х·8·х:9, 16/9 х = 64 => х = 6.

Треугольник АОМ – равносторонний, все стороны = 6. Значит все углы = 60°.

В АОС: О = 90°, А = 60°, С = 30°. Катет, лежащий против угла 30°, равен половине гипотенузы.

Получаем, что АС = 2·АО = 6·2=12.

Точка О является основанием высоты, проведённой из вершины тупого угла А треугольника АВС к стороне ВС. Окружность с центром в точке О и радиусом ОА пересекает прямые АВ и АС в точках Р и М, отличных от А, соответственно. Найдите АС, если АВ =40, АР = 20, АМ = 32.

В АВС биссектриса ВЕ и медиана АМ перпендикулярны и имеют одинаковую длину, равную 60. Найдите стороны треугольника АВС.

Треугольники АВО и МВО равны по общему катету ВО и острому углу при вершине В (ВЕ – бис-са угла В). Значит АВ=ВМ=0,5ВС и АО=ОМ=30. ВО – медиана, бис-са и высота в равнобедренном треугольнике АВМ.

Пусть АВ = х, АЕ=к, АС=у, тогда ВМ=2х, ЕС=у-к. Для бис-сы ВЕ АВС верно равенство:

АЕ : АВ = ЕС : ВС или к : х = (у-к) : (2х) или 2к = у-к, 3к = у, к = 1/3 у.

Для медианы АВС верно равенство: АМ = АВ2 + АС2 — ВС460 = х2 + у2 — 4х4,

Для бис-сы ВЕ АВС верно равенство:

3600 = х·2х – 1/3 у·2/3 у,

2х — 29 7200+х2=3600,х = 1513, у= 7200+ 2925 = 10125, у = 455.

Получаем, что АВ = 1513, АС = 455, ВС = 3013.

Ответ: АВ = 1513, АС = 455, ВС = 3013.

Аналогичная задача В треугольнике АВС биссектриса ВЕ и медиана АД перпендикулярны и имеют одинаковую длину равную 168. Найдите стороны треугольника АВС

Ответ: AB = 4213; BC = 8413; AC = 1265.

Задания из Ященко 30 вариантов

Углы при одном из оснований трапеции равны 19° и 71°, а отрезки, соединяющие середины противоположных сторон, равны 12 и 10. Найти основания трапеции.

1803400106680002438400939800073660011938001587500106680 В Т С

Трапеция АВСD, А=19°, угол D=71°, МН-средняя линия = 12, М € АВ, Н € СD, АМ=МВ, СН=НD, ТР=10, Т € ВС, Р € АD, ВТ=ТС, АР=РD, точка О пересечение МН и ТР, МО=ОН=МН/2=12/2=6, ТО=ОР=ТР/2=10/2=5.

Продлеваем боковые стороны до пересечения их в точке К, треугольник АКD прямоугольный, угол К=180° — А- D =180°-19°-71°=90°.

Треугольник МНК прямоугольный, КО — медиана=1/2гипотенузы МН=12/2=6, КТ=КО-ТО=6-5=1, треугольник ВКС прямоугольный, КТ-медиана=1/2гипотенузыВС, ВС=2*КТ=2*1=2, КР-медиана в прямоугольном треугольнике АКD=1/2гипотенузы АD, АD=2*КР=2*(КТ+ТР)=2*(1+10)=22.

Аналогичная задача Углы при одном из оснований трапеции, равны 44 и 46 градусов, а отрезки, соединяющие середины противоположных сторон равны 14 и 6. Найдите основания трапеции.

«Времвремя Наименование дела Судебные акты 1и 2 инст. 09-00 к 05-1778/16 ГД И: Сейдибалиева Г.С.О: Кок-Ой а/окмоту о восстановлении на работе н/ж: Главы Кок-Ой айыльного окмоту – Узгенова С. решение Таласского райсуда от 05.04.16г. – иск оставить без удовлетворения решение Таласского облсуда от 30.08. »

«Women, nationalism and the Russian right, 1905-17Abstract: This essay examines the activity of women in the Russian organized right between 1905 and 1917. It is particularly concerned with the scale of the female membership of the right-wing movement, and their connection to phil. »

«Эксплуатация xbox 360Подключение беспроводного джойстика к Xbox 360 Slim: Включите xbox 360 Slim. Вставьте в джойстик батарейки типа AA. Нажмите и удерживайте нажатой кнопку «Guide» на джойстике. »

«Попробую изложить, что готово, а что ещё нужно сделать. Чтобы было проще ориентироваться, буду отписываться прямо по файлам исходников.-— Основной проект-— api_common.py Тут сделана попытка сделать обёртку для вывода сообщений об ошибках при использовании API. Наверное, велосипед, но ничего го. »

«Урок 9. Группирование элементов. Поля и отступы. Рамки. Размеры элементов. Всплывающие элементыГруппирование элементов с помощью classПредположим, у нас есть два списка ссылок сортов винограда для белого и для красного вина. HTML-код может быть таким:

Виноград для белого вина:

2018 www.el.z-pdf.ru — «Библиотека бесплатных материалов — онлайн документы»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 2-3 рабочих дней удалим его.

Видео:ОГЭ по математике. 9 класс. Задача 26. Вариант 5.Скачать

Окружность радиус внешний 45 55

Видео:Геометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать

Как посчитать длину окружности

Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Онлайн калькулятор

Как посчитать длину окружности зная диаметр

Какая длина у окружности если

Какова длина окружности (С) если её диаметр d?

Формула

С = π⋅d , где π ≈ 3.14

Пример

Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная радиус

Какая длина у окружности если

Какова длина окружности (С) если её радиус r?

Формула

С = 2⋅π⋅r , где π ≈ 3.14

Пример

Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная её площадь

Какая длина у окружности если

Какова длина окружности (С) если её площадь S?

Формула

С = 2π⋅ √ S /_π , где π ≈ 3.14

Пример

Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.

Видео:Радиус и диаметрСкачать

Как рассчитать периметр круга или длину окружности

На данной странице калькулятор поможет рассчитать периметр круга или длину окружности онлайн. Для расчета задайте радиус или диаметр.

Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.

Видео:Задача 25 (Разбор задачи ОГЭ по математике)Скачать

Окружности радиусов 45 55

Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Окружности радиусом 45 и 55 касаются внешним образом?

Геометрия | 5 — 9 классы

Окружности радиусом 45 и 55 касаются внешним образом.

Точки a и b лежат на первой окружности, точки c и d — на второй.

При этом ِac и bd — общие касательные окружностей.

Найдите расстояние между прямыми ab и cd.

Касательные пересекутся в точке (обозначим) M

центры окружностей (вписанных в угол между касательными)

лежат на биссектрисе этого угла

радиусы, проведенные в точки касания, перпендикулярны касательным))

биссектриса будет и высотой и медианой в равнобедренных треугольниках CMD (AMB) т.

К. отрезки касательных, проведенные из одной точки, равны))

получили подобные прямоугольные треугольники.

Искомое расстояние = 99.

Видео:ОГЭ 2023 Ященко 4 вариант ФИПИ школе полный разбор!Скачать

Окружности радиусов 12 и 20 касаются внешним образом?

Окружности радиусов 12 и 20 касаются внешним образом.

Точки А и В лежат на первой окружности, точки С и D — на второй.

При этом АС и BD — общие касательные окружностей.

Найдите расстояние между прямыми АВ и CD.

Видео:Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей?

Окружности радиусов 36 и 45 касаются внешним образом точки a и b лежат на первой окружности точки C и D на второй при этом AC и BD общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C?

Две окружности с центрами O и O1, радиусы которых 3 и 5, касаются внешним образом в точке C.

Прямая AB касается окружности меньшего радиуса в точке A, а другой — точке B.

Через точку C проведена касательная, которая пересекает прямую AB в точке D.

А) Докажите, что вокруг четырёхугольника AOCD можно описать окружность

б) Найдите радиус этой окружности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружности радиусов 45 и 90 касаются внешним образом?

Окружности радиусов 45 и 90 касаются внешним образом.

Точки A и B лежат на первой окружности, точки C и D на второй .

При этом AC и BD – общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Видео:ОГЭ 2023 Ященко 2 вариант ФИПИ школе полный разбор!Скачать

Прямая, проходящая через точку А, касается окружности радиуса 3 в точке К?

Прямая, проходящая через точку А, касается окружности радиуса 3 в точке К.

Найдите расстояние от точки А до ближайшей к ней точки окружности, если АК = 4.

Видео:1 2 4 сопряжение окружностейСкачать

Решите пожалуйста?

Две окружности разных радиусов касаются друг друга внешним образом.

Две их общие касательные, которые не проходят через точку касания окружностей, касаются окружности меньшего радиуса в точках A и B, а окружности большего радиуса — в точках C и D.

При этом точки A и C лежат на одной касательной, а B и D на другой касательной.

Найдите расстояние между прямыми AB и CD, если радиусы окружностей равны 1, 5 и 6.

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

О₁ и О₂ — центры двух касающихся внешнем образом окружностей?

О₁ и О₂ — центры двух касающихся внешнем образом окружностей.

Прямая О₁О₂ пересекает первую окружность (с центром в точке О₁) в точке А.

Определите диаметр второй окружности, если радиус первой равен 5 см, а касательная, проведенная из точки А ко второй окружности, образует с прямой О₁О₂ угол в 30ᵒ.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

26 Окружности радиусов 22 и 99 касаются внешним образом?

26 Окружности радиусов 22 и 99 касаются внешним образом.

Точки А и В лежат на первой окружности, точки С и В — на второй.

При этом АС и BD — общие касательные окружностей.

Найдите расстояние между прямыми АВ и CD.

Видео:Разбор 3 варианта из сборника Ященко. Зонты | Математика ОГЭ 2023 | УмскулСкачать

Две окружности касаются внешним образом в точке М?

Две окружности касаются внешним образом в точке М.

К этим окружностям проведены две общие касательные, не проходящие через М и касающиеся окружностей в точках A, B, C и D.

Найдите площадь четырехугольника ABCD, если радиусы окружностей равны 60 и 15.

Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Окружности радиусов 4 и 60 касаются внешним образом?

Окружности радиусов 4 и 60 касаются внешним образом.

Точки A и B лежат на первой окружности, точки C и D – на второй.

При этом AC и BD – общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

Вы находитесь на странице вопроса Окружности радиусом 45 и 55 касаются внешним образом? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Решение №2523 Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D …

Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Источник: ОГЭ Ященко 2022 (50 вар)

Построим рисунок по условию, + проведём радиусы: ОA , ОF , OB , EF , EC , ED , построим перпендикуляры AK ⊥ CD , OP ⊥ EC :

AK – искомое расстояние между прямыми АВ и CD .
ΔCAK∼ΔPOE, по двум равным углам (∠CKA=∠OPE = 90°, ∠CAK = ∠POE, т.к. АС||OP, AK||OE). Запишем соотношение сторон:

Выразим АК :

Найдём ОЕ, как сумму двух радиусов:

OE = OF + EF = 25 + 100 = 125

AOPC – прямоугольник (EC⊥AC, OA⊥AC, как радиусы и касательная), противоположные стороны равны:

ОА = РС = 25
АС = ОР

Найдём EP, как разность двух радиусов:

EP = EC – PC = EC – OA = 100 – 25 = 75

В прямоугольном ΔОРЕ по теореме Пифагора найдём ОР :

ОР 2 = ОE 2 – EP 2 = 125 2 – 75 2 = (125 – 75)·(125 + 75) = 50·200 = 10000

Найдём искомое расстояние АК :

💥 Видео

Вся геометрия за 45 минут | Геометрия 7-9 классыСкачать

Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

Профильный ЕГЭ 2024. Задача 16. Касающиеся окружностиСкачать