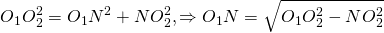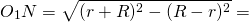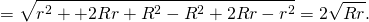Окружности o1 и o2 касаются внешним образом (6 видео)

Окружности o1 и o2 касаются внешним образом

2021-11-14
Окружности с центрами $O_$ и $O_$ касаются внешним образом. В точках $A$ и $B$ их касается внешним образом третья окружность. Докажите, что прямая $AB$ проходит через точку пересечения общих внешних касательных к первым двум окружностям.

Пусть $r$ и $R$ — радиусы окружностей с центрами $O_$ и $O_$ соответственно. Предположим, что $rlt R$. Общие касательные к этим окружностям пересекаются на линии центров, т.е. на прямой $O_O_$, в некоторой точке $Q$. Пусть прямая $AB$ пересекает эту прямую в точке $P$. Докажем, что $O_P=O_Q$. Отсюда будет следовать утверждение задачи.
Пусть прямая, проходящая через точку $Q$, касается окружностей с центрами $O_$ и $O_$ в точках $C$ и $D$ соответственно. Опустим перпендикуляр $O_F$ на $O_D$. Тогда

Прямоугольные треугольники $O_CQ$ и $O_FO_$ подобны, поэтому $frac<O_C><O_Q>=frac<O_F><O_O_>$. Следовательно,

Пусть $O$ — центр третьей окружности, $x$ — её радиус. Применив теорему Менелая (см. 5231) к треугольнику $OO_O_$ и прямой $AB$, получим, что

Значит, $frac<O_P><O_P+R+r>=frac$. Отсюда $O_P=frac=O_Q$. Следовательно, прямые $CD$ и $AB$ пересекают линию центров $O_O_$ в одной и той же точке. Что и требовалось доказать.

Содержание

Задание №1003
Условие
Решение
Окружности касаются внешним образом
🔍 Видео

Видео:Геометрия Две окружности с центрами O1 и O3 и радиусами 4,5 и 2,5 касаются друг с другом внешнимСкачать

Задание №1003

Видео:ОГЭ № 25. "Окружности касаются внешним образом... "Скачать

Условие

Две окружности, с центрами O_ и O_ соответственно касаются внешним образом. Из точки O_ проведена касательная O_K ко второй окружности ( K — точка касания ) , а из точки O_ проведена касательная O_L к первой окружности ( L — точка касания ) , точки касания K и L лежат по разные стороны от прямой O_O_.

а) Докажите, что angle O_KL=angle O_O_L.

б) Найдите радиус меньшей окружности, если дополнительно известно, что он в 4 раза меньше радиуса большей окружности, а площадь четырёхугольника O_KO_L равна 54+9sqrt.

Видео:Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать

Решение

а) По свойству касательной к окружности O_L perp O_L и O_K perp O_K. Прямоугольный bigtriangleup O_O_K вписан в некоторую окружность с диаметром O_O_.

Аналогично прямоугольный bigtriangleup O_O_L вписан в некоторую окружность с тем же диаметром. Следовательно, bigtriangleup O_O_K и O_O_L вписаны в одну и ту же окружность, то есть точки O_, O_, K , L лежат на окружности с диаметром O_O_. Значит, angle O_O_L и angle O_KL — вписанные и опираются на одну и ту же дугу O_L. Отсюда, angle O_KL=angle O_O_L.

б) Пусть O_L — радиус меньшей окружности. Обозначим его через r . Следовательно, O_K=4r. Тогда O_O_=r+4r=5r. Отсюда из bigtriangleup O_LO_ по теореме Пифагора O_L=sqrt=2sqrtr. Из bigtriangleup O_KO_ по теореме Пифагора O_K=sqrt=3r.

Из условия следует, что S_<O_KO_L>=54+9sqrt. Тогда (6+sqrt)r^2=54+9sqrt, (6+sqrt)r^2=9(6+sqrt), r=3.

Видео:Геометрия Две окружности радиуса R с центрами O1 и O2 касаются друг друга. Их пересекает прямаяСкачать

Окружности касаются внешним образом

Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Соединим центры окружностей — точки O₁ и O₂ — с точками A и C соответственно.

Обозначим O₁A=r, O₂C=R.

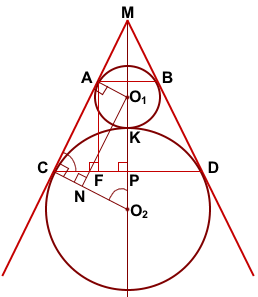
Проведём перпендикуляр AF к прямой CD и перпендикуляр O₁N к прямой CO₂.

AF — искомое расстояние между прямыми AB и CD.

Четырёхугольник AO₁NC — прямоугольник (так как у него три угла прямые).

Рассмотрим прямоугольный треугольник O₁O₂N.

Продлим касательные AC и BD до пересечения в точке M. Проведём луч MO₂.

Окружности с центрами в точках O₁ и O₂ вписаны в угол CMD, значит MP — биссектриса угла CMD.

MC=MD (как отрезки касательных, проведённых из одной точки). Значит треугольник CMD — равнобедренный с основанием CD. Следовательно, биссектриса MP является также его высотой.

В прямоугольном треугольнике CMP ∠MCP=90°-∠CMP.

В прямоугольном треугольнике CMO₂ ∠CO₂M=90°-∠CMP.

Отсюда ∠MCP=∠CO₂M. Следовательно, прямоугольные треугольники AFC и O₁NO₂ подобны (по острому углу).