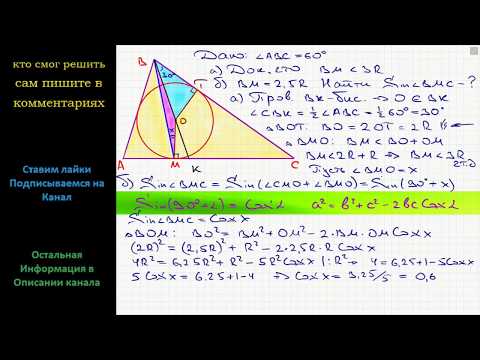
Видео:Геометрия В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касаетсяСкачать
Ваш ответ
Видео:Геометрия Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. НайдитеСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,997
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность вписанная в треугольник abc касается стороны ac
Окружность, вписанная в треугольник ABC, касается сторон BC и AC в точках M и N соответственно, E и F — середины сторон AB и AC соответственно. Прямые MN и EF пересекаются в точке D.
а) Докажите, что треугольник DFN равнобедренный.
б) Найдите площадь треугольника BED, если AB = 28 и ∠ABC = 60°.
а) Поскольку CM = CN, треугольник MCN равнобедренный. Прямые EF и BC параллельны, поэтому треугольник DFN подобен треугольнику MCN, следовательно, треугольник DFN также равнобедренный: DF = NF.
б) Обозначим BC = a, AC = b, AB = c. Пусть p — полупериметр треугольника ABC. Предположим, что a > c. Тогда
Значит, то есть треугольник BED равнобедренный.
Аналогично для a ≤ c.
Поскольку прямые ED и BC параллельны,
Следовательно,
Ответ: б)
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Геометрия Вписанная окружность треугольника ABC касается сторон AB BC и AC в точках M N и KСкачать  Задание №997Видео:Окружность вписанная в прямоугольный треугольник АВС касается катетов АС и ВС в точках М и N соответСкачать  УсловиеОкружность, вписанная в остроугольный треугольник ABC , касается сторон AB и AC в точках E и F . а) Докажите, что центр окружности, вписанной в треугольник AEF , лежит на окружности, вписанной в треугольник ABC . б) Найдите расстояние между центрами этих окружностей, если AB=11, AC=14, BK=3,08, где K — точка пересечения стороны BC и биссектрисы, проведённой из вершины A . Видео:№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать 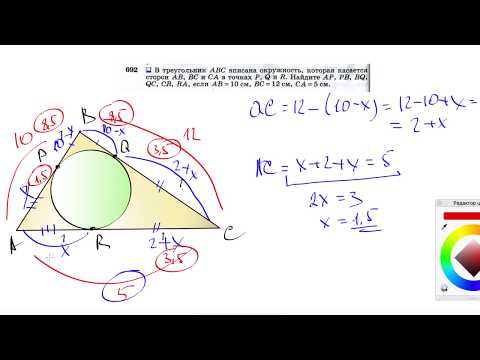 Решениеа) Пусть точка O — центр вписанной окружности треугольника ABC . O лежит на биссектрисе AK . Биссектриса AK пересекает дугу EF в точке P , а отрезок EF — в точке D . AE=AF как отрезки касательных, проведенных к окружности из одной точки. Отсюда, bigtriangleup EAF — равнобедренный, значит, биссектриса AD — медиана и высота. bigtriangleup PDE=bigtriangleup PDF по двум катетам ( ED=DF, PD — общая сторона). Из равенства треугольников следует PE=PF, а так как равные хорды стягивают равные дуги, то smile PE=smile PF. Докажем, что P — центр вписанной окружности треугольника EAF . angle AFP=frac smile PF как угол между касательной AF и хордой PF . angle EFP=frac smile PE как вписанный. Так как smile PF=smile PE, то angle AFP=angle EFP, значит, FP — биссектриса угла AFE . Таким образом, P — точка пересечения биссектрис AD и FP треугольника AEF , следовательно, P — центр вписанной окружности. б) По условию AK — биссектриса bigtriangleup ABC , проведённая из вершины A . По свойству биссектрисы имеем frac=frac, Пусть O — центр вписанной окружности в bigtriangleup ABC, r — радиус этой окружности, p — полупериметр bigtriangleup ABC. Расстояние между центрами окружностей OP=r=frac<3sqrt>. 🎬 ВидеоОГЭ, геометрия, задачи повышенной сложности. Часть 3Скачать  ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать  ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать  Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать  Задание 16 ЕГЭ по математике #10Скачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  15 задание треугольники огэ по математике / маттаймСкачать  Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать  Геометрия В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причёмСкачать 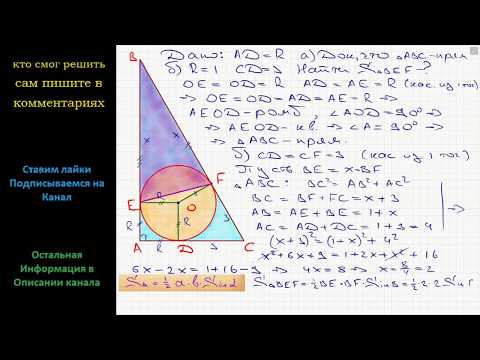 8 класс, 38 урок, Вписанная окружностьСкачать  Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 классСкачать  ОГЭ 2022 Демоверсия. 25 задание | Основание AC равнобедренного треугольника ABC равно 12.....Скачать  Окружность, вписанная в треугольникСкачать  Геометрия Точка O центр окружности вписанной в треугольник ABC BC = a AC = b угол AOB = 120 НайдитеСкачать  |
