Геометрия | 5 — 9 классы
Окружность разделена двумя точками на две дуги.
Найдите градусную меру каждой дуги, если одна из них в 9 раз больше другой.
Решение в приложении …….
- Две точки делят окружность на две дуги градусная мера одной дуги на 60 градусов больше другой?
- Длина дуги окружности радиусом 24 см равна 3п см?
- На окружности отмечены точки M и K так что градусная мера одной из оброзовавшихся дуг на 40 больше градусной меры другой чему равны величины данных дуг?
- Найдите градусную меру двух дуг окружности, на которые делят её точки, если градусная мера одной из дуг на 100 градусов больше градусной меры другой?
- СРОЧНООО ПОМОГИТЕ ПОЖАЛУЙСТА ПРОШУУУ 1) Найдите градусную меру центрального угла, если соответствующая ему дуга составляет 2 / 9 дуги окружности?
- Найдите градусные меры дуг окружности, на которые ее делит диаметр этой окружности?
- Найдите длину дуги окружности радиуса 9м, если градусная мера дуги равна 120°?
- Полуокружность разделена на 3 равных частей?
- Найдите градусную меру дуги, если окружность разделена на 15 равных частей?
- Две точки окружности разделили ее на две дуги?
- Окружность и круг
- Содержание
- Окружность
- Радиус
- Диаметр
- Части круга и окружности
- § 2. Центральные и вписанные углы
- Градусная мера дуги окружности
- Теорема о вписанном угле
- Задачи
- 📸 Видео
Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Две точки делят окружность на две дуги градусная мера одной дуги на 60 градусов больше другой?
Две точки делят окружность на две дуги градусная мера одной дуги на 60 градусов больше другой.
Какова градусная мера каждой дуги.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Длина дуги окружности радиусом 24 см равна 3п см?
Длина дуги окружности радиусом 24 см равна 3п см.
Найдите градусную меру дуги.
Видео:Вершины треугольника делят окружность на три дуги, длины которых относятся как 3:4:11Скачать

На окружности отмечены точки M и K так что градусная мера одной из оброзовавшихся дуг на 40 больше градусной меры другой чему равны величины данных дуг?
На окружности отмечены точки M и K так что градусная мера одной из оброзовавшихся дуг на 40 больше градусной меры другой чему равны величины данных дуг.
Видео:Вписанные углы в окружностиСкачать

Найдите градусную меру двух дуг окружности, на которые делят её точки, если градусная мера одной из дуг на 100 градусов больше градусной меры другой?
Найдите градусную меру двух дуг окружности, на которые делят её точки, если градусная мера одной из дуг на 100 градусов больше градусной меры другой.
Пожалуйста помогите, срочно нужно.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

СРОЧНООО ПОМОГИТЕ ПОЖАЛУЙСТА ПРОШУУУ 1) Найдите градусную меру центрального угла, если соответствующая ему дуга составляет 2 / 9 дуги окружности?
СРОЧНООО ПОМОГИТЕ ПОЖАЛУЙСТА ПРОШУУУ 1) Найдите градусную меру центрального угла, если соответствующая ему дуга составляет 2 / 9 дуги окружности.
2) Найдите градусную меру вписанного угла, если он опирается на дугу, которая составляет 5 / 9 дуги окружности.
Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Найдите градусные меры дуг окружности, на которые ее делит диаметр этой окружности?
Найдите градусные меры дуг окружности, на которые ее делит диаметр этой окружности.
Видео:Окружнось. Зависимость длины хорды, от длины дуги.Скачать

Найдите длину дуги окружности радиуса 9м, если градусная мера дуги равна 120°?
Найдите длину дуги окружности радиуса 9м, если градусная мера дуги равна 120°.
Видео:Длина дуги окружности. 9 класс.Скачать

Полуокружность разделена на 3 равных частей?
Полуокружность разделена на 3 равных частей.
Найдите градусную меру каждой дуги и центрального угла, соответствующего этой дуге.
Видео:Окружность данного радиуса, проходящей через две заданные точкиСкачать
Найдите градусную меру дуги, если окружность разделена на 15 равных частей?
Найдите градусную меру дуги, если окружность разделена на 15 равных частей.
Можно пожалуйста с рисунком).
Видео:Длина отрезкаСкачать

Две точки окружности разделили ее на две дуги?
Две точки окружности разделили ее на две дуги.
Найдите их градусные меры, если угол между радиусами, проведенными в эти точки, равен 110°.
Вы находитесь на странице вопроса Окружность разделена двумя точками на две дуги? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Сторона треугольника a = 14, а высота h = 31 площадь треугольника найдем по формуле S = a×h / 2 подставим S = 14×31 / 2 = 434 / 2 = 217.
Угол BAC = 112 ( вертикаль) т. К. AB = AC углы ABC = ACB ABC = ACB = (180 — 112) / 2 = 34 угол x = 180 — 34 = 146.
СДВ = 63. СВД = 37. Они равные .
14)угол N = 99° угол К = 54° угол М = 27° 15)так как каждая сторона треугольника меньше чем сумма двох других сторон то 1 и 3 1) рассмотрим треугольники АВD и BCD так как АВ = СD, ВС = АD и они имеют общую сторону ВD то они равны за 3 признаком(тремя..
Если все боковые ребра наклонены под одним углом к основанию пирамиды, все боковые ребра равны, а вершина пирамиды проецируется в центр описанной около основания окружности. Центр окружности, описанной около прямоугольного треугольника лежит на сере..
Вычислим угол между плоскостями 2x — y + 3z + 0. 5 = 0 и 4x — 2y + 3z + 1 = 0 cosα = |A1·A2 + B1·B2 + C1·C2| / (√A1² + B1² + C1²√A2² + B2² + C2²) cosα = |2·4 + ( — 1)·( — 2) + 3·3| / (√(2² + ( — 1)² + 3²) * √(4² + ( — 2)² + 3²)) = = |8 + 2 + 9| / (√..
А) 15 — 3 = 12 12 : 2 = 6 6 + 3 = 9 АС = 9 ВС = 6 б) 15 : 3 = 5 5 * 2 = 10 АС = 10 ВС = 5 в) 15 : 5 = 3 3 * 2 = 6 3 * 3 = 9 АС = 6 ВС = 9.
1 — ый угол это х 2 — ой угол 3х 3 — ий угол 3х + 33 Их сумма 180 градусов, следовательно х + 3х + 3х + 33 = 180 7х = 180 — 33 7х = 147 х = 21 Т. Е 1 — ый угол 21 градус 2 — ой угол 21 * 3 = 63 градуса 3 — ий угол 21 * 3 + 33 = 96 градусов Вот и всё..
AB = AC ^ 2 + CB ^ 2 AB = 36 + 36 AB = 72 AB = 36 Вроде так.
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Окружность и круг
Содержание
В древние времена люди смотрели на небо и видели там круглое Солнце, круглую Луну. Они придавали кругу мистическое значение и считали его очень красивым. Изображение круга можно увидеть на наскальных рисунках.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Окружность
Судя по древним изображениям, люди изобрели циркуль, с помощью которого можно было чертить ровные круги, уже три тысячи лет назад. Циркуль даже упоминается в мифах Древней Греции.
Если установить ножку циркуля с иглой в какую-либо точку, а ножку с грифелем или карандашом повернуть вокруг той точки, у нас получится замкнутая линия. Она называется окружность.
Окружность состоит из множества точек, расположенных очень близко друг к другу. И какую бы точку на окружности мы не взяли, расстояние от этой точки до центральной точки (той, в которую мы втыкали иглу циркуля) будет одинаковым.
Окружность — замкнутая кривая, которая состоит из всех точек на плоскости, одинаково удалённых от заданной точки, лежащей в той же плоскости, что и кривая; эта точка называется центром окружности.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Радиус
Поставим точку О, затем начертим вокруг неё окружность. На окружности поставим точку А. Это можно сделать в любом месте, где захотите. Теперь соединим точки, у нас получится отрезок ОА. Теперь поставим на окружности вторую точку, В, и тоже соединим её с центром. Сравним отрезки ОА и ОВ. Они равны.
Сколько бы мы ни ставили точек на окружности и сколько бы ни соединяли их с центром, у нас будут получаться равные отрезки.
Отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, называется радиус.
Все радиусы окружности равны между собой.
Латинское слово radius переводится как «спица колеса». Действительно, ведь все спицы у колеса соединены с центром и все равны.
Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Диаметр
Теперь проведём линию от точки С через центр окружности до её противоположного края. Отрезок СD состоит из двух радиусов: СО и ОD. По размеру он вдвое длиннее радиуса. Такой отрезок называется диаметр.
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
Помните, мы говорили, что плоскость бесконечна? Но, прочертив на ней окружность, мы делим плоскость на две части. Одна часть – за пределами окружности – так и остаётся бесконечной. А вторая, маленькая, оказывается ограничена пределами окружности и лежит внутри неё.
Часть плоскости вместе с самой окружностью называют кругом.
Это как если бы мы взяли большой лист бумаги, нарисовали на нём кружок и вырезали его ножницами.
Круг тоже состоит из множества точек, и все они лежат на нашей маленькой плоскости. Расстояние от этих точек до центра круга не превышает радиус.
Видео:Решение задач на тему центральные и вписанные углы.Скачать

Части круга и окружности
Рассмотрим рисунок 8.
Диаметр разделяет круг на два равных полукруга, а окружность – на две полуокружности.
Это как если бы мы разрезали пополам пирог с тоненькой корочкой. Часть с ягодами – круг, а корочка – окружность.
Часть окружности называется дугой
Теперь мы можем сформулировать определение полукруга и полуокружности:
Полукруг – часть круга, ограниченная диаметром и дугой, лежащей между концами диаметра
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром
Таким образом, полуокружность – это тоже дуга, но не всякая дуга – полуокружность.
Точки А и В на рисунке 10 разделяют окружность на две части, две дуги. Сами точки называют концами дуг.
А вот с таким делением круга, как на рисунке 11, вы наверняка хорошо знакомы. Такой кусочек называется «сектор». Можете попробовать дать определение сектора?
Показать определение сектора
Сектор — часть круга, ограниченная дугой и двумя радиусами
Давайте проверим, хорошо ли вы запомнили части круга.
А вот ещё один хорошо знакомый вам пример окружности – циферблат. Эта окружность разделена на 60 равных делений, и когда минутная стрелка минует очередное деление, это означает, что прошла минута. А больших делений 12, каждое соответствует часу.
Видео:Углы, связанные с окружностьюСкачать

§ 2. Центральные и вписанные углы
Градусная мера дуги окружности
Отметим на окружности две точки А и В. Они разделяют окружность на две дуги. Чтобы различать эти дуги, на каждой из них отмечают промежуточную точку, например L и М (рис. 214). Обозначают дуги так: 


Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности. На рисунке 215, а изображены две полуокружности, одна из которых выделена цветом.
Угол с вершиной в центре окружности называется её центральным углом. Пусть стороны центрального угла окружности с центром О пересекают её в точках А к В. Центральному углу АОВ соответствуют две дуги с концами А и В (рис. 215). Если ∠АОВ развёрнутый, то ему соответствуют две полуокружности (рис. 215, а). Если ∠АОВ неразвёрнутый, то говорят, что дуга АВ, расположенная внутри этого угла, меньше полуокружности. На рисунке 215, б эта дуга выделена цветом. Про другую дугу с концами А и В говорят, что она больше полуокружности (дуга ALB на рисунке 215, в).
Дугу окружности можно измерять в градусах. Если дуга А В окружности с центром О меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла АОВ (см. рис. 215, а, б). Если же дуга АВ больше полуокружности, то её градусная мера считается равной 360° — ∠АОВ (см. рис. 215, в).
Отсюда следует, что сумма градусных мер двух дуг окружности с общими концами равна 360°.
Градусная мера дуги АВ (дуги ALB), как и сама дуга, обозначается символом 





Теорема о вписанном угле
Угол, вершина которого лежит на окружности, а стороны пересекают, окружность, называется вписанным углом.
На рисунке 217 угол АВС вписанный, дуга АМС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу АМС. Докажем теорему о вписанном угле.
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Пусть ∠ABC — вписанный угол окружности с центром О, опирающийся на дугу АС (рис. 218). Докажем, что 
1) Луч ВО совпадает с одной из сторон угла АВС, например со стороной ВС (рис. 218, а). В этом случае дуга АС меньше полуокружности, поэтому ∠AOC = 
Отсюда следует, что
2∠1 = 
2) Луч ВО делит угол АВС на два угла. В этом случае луч ВО пересекает дугу АС в некоторой точке D (рис. 218, б). Точка D разделяет дугу АС на две дуги: 

Складывая эти равенства, получаем:
3) Луч ВО не делит угол ABC на два угла и не совпадает со стороной этого угла. Для этого случая, пользуясь рисунком 218, в, проведите доказательство самостоятельно.
| Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 219). |
| Вписанный угол, опирающийся на полуокруж ность, — прямой (рис. 220). |
Используя следствие 1, докажем теорему о произведении отрезков пересекающихся хорд.
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Пусть хорды АВ и CD пересекаются в точке Е (рис. 221). Докажем, что
Рассмотрим треугольники ADE и СВЕ. В этих треугольниках углы 1 и 2 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 3 и 4 равны как вертикальные. По первому признаку подобия треугольников ΔADE ∼ ΔCBE. Отсюда следует, что 
Задачи
649. Начертите окружность с центром О и отметьте на ней точку А. Постройте хорду АВ так, чтобы: a) ∠AOB = 60°; б) ∠AOB = 90°; в) ∠AOB = 120°; г) ∠AOB = 180°.
650. Радиус окружности с центром О равен 16. Найдите хорду АВ, если: a) ∠AOB = 60°; б) ∠AOB = 90°; в) ∠AOB =180°.
651. Хорды АВ и CD окружности с центром О равны.
а) Докажите, что две дуги с концами А и В соответственно равны двум дугам с концами С и D.
б) Найдите дуги с концами С и D, если ∠AOB = 112°.
652. На полуокружности АВ взяты точки С и D так, что 

653. Найдите вписанный угол АВС, если дуга АС, на которую он опирается, равна: а) 48°; б) 57°; в) 90°; г) 124°; д) 180°.
654. По данным рисунка 222 найдите х.
655. Центральный угол АОВ на 30° больше вписанного угла, опирающегося на дугу АВ. Найдите каждый из этих углов.
656. Хорда АВ стягивает дугу, равную 115°, а хорда АС — дугу в 43°. Найдите угол ВАС.
657. Точки А и В разделяют окружность на две дуги, меньшая из которых равна 140°, а большая точкой М делится в отношении 6 : 5, считая от точки А. Найдите угол ВАМ.
658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая AD, проходящая через центр О (D — точка на окружности, О лежит между А и D). Найдите ∠BAD и ∠ADB, если 
659. Докажите, что градусные меры дуг окружности, заключённых между параллельными хордами, равны.
660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32°. Большая дуга окружности, заключённая между сторонами этого угла, равна 100°. Найдите меньшую дугу.
661. Найдите острый угол, образованный двумя секущими, проведёнными из точки, лежащей вне окружности, если дуги, заключённые между секущими, равны 140° и 52°.
662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если 

663. Отрезок АС — диаметр окружности, АВ — хорда, МА — касательная, угол МАВ острый. Докажите, что ∠MAB = ∠ACB.
664. Прямая AM — касательная к окружности, АВ — хорда этой окружности. Докажите, что угол МАВ измеряется половиной дуги АВ, расположенной внутри угла МАВ.
665. Вершины треугольника АВС лежат на окружности. Докажите, что если АВ — диаметр окружности, то ∠C > ∠A и ∠C > ∠B.
666. Хорды АВ и CD пересекаются в точке Е. Найдите ED, если:
а) АЕ = 5, ВЕ = 2, СЕ = 2,5; б) АЕ = 16, ВЕ = 9, CE = ED;
в) АЕ = 0,2, BE = 0,5, СЕ = 0,4.
667. Диаметр АА1 окружности перпендикулярен к хорде ВВ1 и пересекает её в точке С. Найдите ВВ1 если АС = 4 см, СА1 = 8 см.
668. Докажите, что перпендикуляр, проведённый из какой-нибудь точки окружности к диаметру, есть среднее пропорциональное для отрезков, на которые основание перпендикуляра делит диаметр.
669. Пользуясь утверждением, сформулированным в задаче 668, постройте отрезок, равный среднему пропорциональному для двух данных отрезков.
670. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекает окружность в точках Р и Q. Докажите, что АВ 2 = АР • AQ.
671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекает окружность в точках С и D. Найдите CD, если: а) АВ = 4 см, АС = 2 см; б) АВ = 5 см, AD = 10 см.
672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекает окружность в точках В1 и С1, а другая — в точках В2 и С2. Докажите, что АВ1 • АС1 = АВ2 • АС2.
673. К данной окружности постройте касательную, проходящую через данную точку вне окружности.
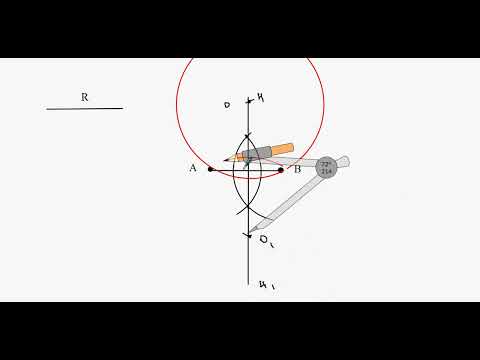
Пусть даны окружность с центром О и точка А вне этой окружности. Допустим, что задача решена и АВ — искомая касательная (рис. 223). Так как прямая АВ перпендикулярна к радиусу ОВ, то решение задачи сводится к построению точки В окружности, для которой ∠ABO прямой. Эту точку можно построить следующим образом: проводим отрезок ОА и строим его середину О1. Затем проводим окружность с центром в точке Ох радиуса О1А. Эта окружность пересекает данную окружность в двух точках: В1В1. Прямые АВ и АВ1 — искомые касательные, так как АВ ⊥ ОВ и АВ1 ⊥ ОВ1. Действительно, углы АВО и АВ1O, вписанные в окружность с центром О1, опираются на полуокружности, поэтому они прямые. Очевидно, задача имеет два решения.
📸 Видео
Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

#4 Самое сложное задание 16 ОГЭ 2021. Углы в окружности. Касательная к окружности.Скачать

Изонить 03 - Основной алгоритм заполнения окружности / Basic Pattern for Filling a CircleСкачать

Расстояние между двумя точками на плоскости.Скачать






















