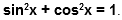Окружность 360 градусов как записать (6 видео)

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Содержание

Единичная окружность в тригонометрии
Почему именно 360 градусов
Алгебра
Числовая и единичная окружность
Откладывание углов на единичной окружности
🎦 Видео

Видео:Почему в окружности 360 градусов? 🤔Скачать

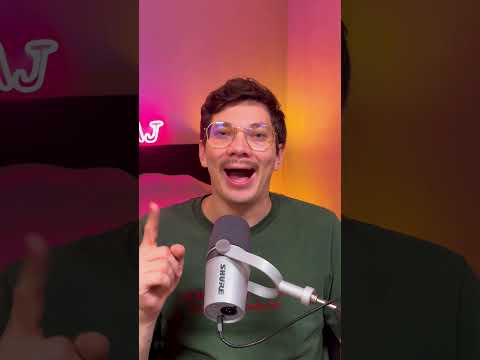
Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

2π радиан = 360°
1 радиан = (360/2π) градусов
1 радиан = (180/π) градусов
360° = 2π радиан
1° = (2π/360) радиан
1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Почему в окружности 360 градусов? #shorts #математика #геометрия #алгебра #репетитор #7классСкачать

Почему именно 360 градусов

В самом деле, почему появилась разметка круга именно 360°? Эта тема является продолжением статьи «Что же такое угол». Как всегда, чтобы поднять настроение нужно почитать мнение ученых. Объяснения детей и ученых слушать одинаково любопытно – они говорят внезапными парадоксами и совершенно не заморачиваются сутью.
К примеру: – «История развития человечества знала разные системы счисления: двоичную, самую древнюю и примитивную, и десятеричную, при которой счет велся по количеству пальцев рук. В Древнем Вавилоне изобрели шестидесятеричную систему счисления. Вавилоняне считали тройками, по числу суставов на каждом пальце левой руки (без большого пальца), то есть до 12. Затем каждый палец правой руки (включая большой) означал 12. Благодаря этому счет продолжался до 60. Число 60 стало в Древнем Вавилоне ритуальным. Позднее ритуальные значения получили и некоторые числа, кратные 60: 300, 360. Так, Кир, древнеперсидский царь, раздробил реку Гиндес, в которой утонул его любимый конь, на 360 ручьев».
Слыхали что-нибудь подобное? В ход пошли костяшки, руки, пальцы, отверстия и прочие выступы. Вот к чему и до чего может привести баловство со счетом – до ритуальности, сакральности и прочих вселенских событий. В этой истории надувания из мухи слона удивительно другое, как простодушно люди не понимают причину и следствие. Причина счёта и удобство счёта им без разницы.
Или же ещё: – «Знаете ли вы, почему в окружности 360° градусов, а не 180° или, скажем, не 300°? Откуда пошла традиция делить окружность на равные части и почему было выбрано именно такое их число? Оказывается, этому делению мы обязаны вавилонянам. Согласно их календарю, продолжительность года составляла 360 дней – именно столько раз, по наблюдениям древних астрономов, солнечный диск укладывался на годичном пути светила. Иными словами, за каждые сутки солнце делало один «шаг». Поэтому вавилоняне и разделили окружность на 360 равных частей, каждую из которых называют градусом (от лат. gradus – шаг, ступень)».

Так эти двоечники не знали сколько дней в году. А мы пользуемся. Куда смотрит общественность? Потом-то они узнали, но так и оставили. Так и мы оставили. А какая проблема, братцы? Разделим круг на 365 долей, и все дела. По счастью и несчастью нашей цивилизации фиолетово, 360 или 365. Ученые – господа, сэры, доны, месье и синьоры не понимают самых простых вещей – градуса, угла, аспекта, нуля, плюс числа, минус числа и т.п. Но при этом не устают развлекать нас глупостями вроде малой и большой бесконечности.

Или: – «Измерять угол градусами это всего лишь традиция такая, обычай».

– «Родители тоже согласны. Можно пойти в ЗАГС, но до этого, по обычаю, невесту нужно украсть!
– Украсть? О, черт, красивый обычай. Ну, а моя-то какая роль?
– Поймать невесту. Сунуть ее в мешок.
– В мешок? Это что, тоже по обычаю? Гениально! Ну-ну?
– И передать кунакам влюбленного джигита.
– Ах, кунакам?
– Так требует обычай. Но учтите, обычай требует, чтобы все было натурально.
Невеста будет сопротивляться, брыкаться, даже кусаться, звать милицию, кричать: «Я буду жаловаться в обком!», – но Вы не обращайте внимания. Это старинный красивый обычай.
– Я понимаю. Не волнуйтесь. Все будет натурально».

И вот мы узнаём про красивый обычай 360-дневного года в Двуречье и Древнем Египте. А для натуральности нам рассказывают байки о поэтапном узнавании подлинного числа дней в году.
Но древний мир Двуречья не знал 360-дневного года в своих календарях. Установить начало календарного года по годичному движению Солнца задача трудная. Куда легче связать счет дней с изменением фаз Луны. Поэтому вначале появился лунный календарь. Так вот в Шумере и Вавилоне затем появился лунно-солнечный календарь. Лунный год состоял из 354 дней. Около 2500 лет до н.э. шумеры пользовались календарем с определенными правилами вставки 13-го месяца, чтобы сохранять на своем месте месяцы, названия которых соответствует определенным сезонам года. Причем вставки делались не произвольно, а согласно положению Солнца на эклиптике.
Ссылка на представление шумеров о ежедневном сдвиге Солнца к востоку на два своих диаметра, около 1°, стала басней, призванной объяснить 360° меру 360-дневным годом. Шумеры, а так же индийцы прекрасно знали, что скорость движения Солнца в течение года меняется. Весна и осень целиком находились в пределах медленной и быстрой частей года, составляя 94,5 и 88,6 суток. Моменты положения Солнца на экваторе, когда начиналась весна или осень, и в точках солнцестояния определялись в Двуречье с точностью до 12 часов. При общих календарных расчетах жрецы считали, что Солнце на большей части своей орбиты, 194°, двигалось, отступая к востоку на 1° в день, а на меньшей – на 56’15», что как раз и позволяло ему завершить свой путь за 365 суток.

Египетский календарь, да, является древнейшим солнечным календарем. Откуда же в нём появляется число 360? Ученых почему-то не смущает подозрительно круглая и грубая ошибочка в пять дней. Уж не костяшки ли тут впереди астрономии?
Но, нет. В результате дальнейших астрономических наблюдений египетские жрецы установили, что продолжительность солнечного года, вот те на, близка к 365 дням. Поэтому и календарь пришлось дополнить пятью днями, греческое название которых – эпагомены – «те, что над годом». По этому поводу обычно приводится легенда, рассказанная Плутархом, о том, как мудрый Тот выиграл у богини Луны от каждого дня 360-дневного года по 172 части – искомые пять дней.
Но и тут у жрецов вышла промашка. Пришлось еще немножко покумекать. «Позже египетские ученые обнаружили, что и вставки пяти дней недостаточно». И если бы египтяне приняли длину года равной 365,25 суток, то они были бы правильные ребята.
В этих эпических поисках правды жизни остается открытым вопрос, что же всё-таки является причиной суточной маеты египтян – счет костяшками или же астрономия?
Да знали египтяне прекрасно, что год состоит из 365,25 дней, но жрецы упорно избегали реформы календаря по своим мотивам, которые к данной теме не относятся. У древних китайцев солнечный год был равен 366 дням. Восходящий на трон фараон должен был давать клятву не менять календаря. Вразумлять жрецов пытались как собственные правители, так и владыки завоевателей. Так царь гиксосов Салитис, завоевавший в XVIII в. до н.э. Египет провёл календарную реформу. Он требовал добавлять каждые четыре года по одному дню, выравнивающему ход времени. Но когда через 100 лет гиксосы были изгнаны из страны, время продолжали считать по календарю, «установленному Тотом».

Тогда в чем тут дело? Шумеры и египтяне прекрасный и способный народ. И много чего полезного сделали. Но при этом нужно понимать, что не они были первыми. Математика круга (МК) была создана задолго до них в палеолите. И в этом отношении они были эпигонами.
Число 360, так же, как 7, 12 и 30 знал весь древний мир без всяких заимствований. И никакой связи с числом дней в году оно не имеет. Это разные и самостоятельные числа. Поэтому и выводить их одно из другого нельзя и бессмысленно. Фактически это число является самым ценным подарком человечеству.
Одними из важнейших указателей на знание МК в палеолите являются многочисленные культовые диски с дырой – плюс круг и минус круг. В неолите они появились как хенджи – круговые насыпь и ров. Таким же прямым указателем является повсеместный культ головы-черепа, который впервые появился уже у Homo erectus и неандертальцев («Вытянутые черепа. Происхождение»). Для этого нужно было знать механизм образования геометрической фигуры аспекта. А, значит, правильно понимать угол, аспект, градус.
Конструкция – череп на длинных костях косым крестом, поставленные на прямоугольное основание, является прообразом храма и алтаря на все времена («Почему мировое дерево, пуп земли, трон, алтарь»). Они соответствуют шумерской концепции «места божества» и «обители божества».
Знаки зодиака, прообразом которых послужили геометрические фигуры больших аспектов, возможно, также достались шумерам в наследство из прошлых времен. Вместе с шумерами ушло понимание МК. Круг 360°, конечно, достался египтянам в наследство. А вот объяснить его они уже не могли, поскольку утратили МК. Отсюда и появилась легенда об увязке числа 360 и 365.

А теперь, почему именно 360. В самом деле, почему круг нельзя разметить на какое-нибудь другое число долей, что от этого изменится? Что нам традиции, возьмем, да разметим. Ну, предположим, на 100 долей. Практично и удобно. Но перед этим надо понять, что дали нам 360°.
Мы уже знаем, что каждый порядковый градус уже является аспектом, углом. Просто потому, что он составляет дистанцию на круге к нулю. Это значит, что можно составить геометрическую фигуру каждого градуса и определить его силу («Доказательство знаков Зодиака»).
И вот на адресах больших знакообразующих градусов через каждые 30° появляются наиболее простые фигуры. Чем они проще, тем более выгодный и сильный градус.
Красные точки – первые точки аспекта. Синие точки – вторые точки аспекта.

1. 0° и 360° – Точка.
2. 30° и 330° –Трапеция короткая, основания которой 60° и 120°.
3. 60° и 300° – Прямоугольник.
4. 90° и 270° – Треугольник равнобедренный.
5. 120° и 240° – Линия вертикальная.
6. 150° и 210°– Трапеция длинная, основания которой 60° и 120°.
7. 180° – Линия горизонтальная.

Доказываем утверждение шумеров и египтян: «То, что внизу подобно тому, что вверху». И наоборот.
Зеркальные по горизонтальной оси градусы 360°, 330°, 300°, 270°, 240°, 210° будут иметь точно такую же фигуру аспекта, как их напарники. В ней только зеркально поменяется порядок первых и вторых точек аспекта. 180° не имеют зеркального плюс напарника.
Число линий, соединяющих эти зеркальные градусы, равно семи.

«То, что справа подобно тому, что слева». Это утверждение звучит более приглушенно, чем первое. К примеру, зеркальные по срединной оси фигуры.
Так и есть.
1. 0° и 180°. Точка и горизонтальная Линия.
2. 30° и 150°. Трапеция короткая и Трапеция длинная.
3. 60° и 120°. Прямоугольник и Линия вертикальная.
4. 90° и 270° – не имеют напарника право-лево. Полное подобие точек. Поэтому, в том числе, вертикальная линия это основное место божества «при исполнении».

Получается, что 8 точек круга являются безусловно наиболее выгодными, поскольку фигуры этих градусов-аспектов отличаются от Трапеции. Это 0° и 180°, 60° и 300°, 90° и 270°, 120° и 240°. Назовем их «Большие градусы». Все остальные градусы имеют фигуру Трапеции разной степени выгодности. Тогда почему шумеры добавили к этой группе еще четыре градуса, открывающих Знаки – 30°, 150°, 210° и 330°? Дело в том, когда в основаниях или сторонах или диагоналях Трапеции появляются угловые расстояния равные Большим градусам, то они выделяют такой градус как умеренно сильный. Их надо отметить. Назовем их выгодные «Малые градусы». И оказывается, что 10-й и 20-й градус каждого Знака является умеренно сильным.
Так вот для Малых выгодных градусов Большим будет что-то одно – или ОСНОВАНИЯ, или СТОРОНЫ, или ДИАГОНАЛИ Трапеции.
А для упомянутой четверки Больших градусов Большими являются ОСНОВАНИЯ (60° и 120°), а также или СТОРОНЫ или ДИАГОНАЛИ Трапеции, что позволяет войти им в Большую лигу. Так для 30° и 330° также Большими являются диагонали Трапеции(90°), а для 150° и 210° Большими являются стороны Трапеции(90°).

По-своему правы были египтяне, когда размечали круг на 36 деканов по 10°. Но в эти деканы попадали как Большие, так и Малые градусы без разницы. Шумеры же выделяли Большие градусы особо как Знаки зодиака. Но тогда пропадали Малые градусы. И всё же каждая разметка оправдана.
Долевое деление круга должно соответствовать числу сильных и слабых точек или сильных и слабых долей. Очевидно, что по обе стороны сильных точек находятся слабые точки, поскольку фигура градуса переходит в невыгодную трапецию. Но нам нужно знать пропорцию интервала такой доли, иначе всё будет приблизительно.
Но, оказывается, что помимо шумерской и египетской разметки круга нужно обязательно выделить градусы каждой середины Знака. Например, на Линии полуквадрата, 45°-315°, и полутароквадрата, 135°-225°, есть довольно сильные точки. Но они, как и прочие Малые градусы, не сильнее, чем 30° и 150°.
Для примера в сравнении показываю фигуру аспекта 40-го градуса и зеркального ему 320-го. (8 – первая). Диагонали Трапеции – тригоны (120°). Вторая фигура примечательна тем, что она немного уступает фигурам Больших градусов, имеющих вид трапеции – 30-у, 330-у и 150-у, 210-у. Это фигура 45-го и 315-го градуса. Точно такая фигура, только зеркальная по вертикальной оси, будет для 135-го и 225-го градуса. Основания Трапеции – это сильные угловые расстояния – 90° и 180°. И они сильнее соответственно, чем основания Трапеции у 30-го и 150-го градуса (60° и 120°). Отличие в том, что диагонали или стороны Трапеции у последних градусов также принадлежат к Большим градусам. Для 30-го градуса это диагонали (90°), а для 150-го градуса это стороны (90°).

И вот эти градусы середины Знака 15°, 45°, 75° и т.д. дают нам пропорции интервалов каждой доли, поскольку по обе стороны от них так же находятся слабые градусы. Эти интервалы-доли отмечаем числами. Пока мы не знаем, что это градус, декада или Знак, но условно будем так называть некие интервалы.

Теперь считаем:
1. В каждом Знаке 4 сильные точки (доли) – 1-я, 10-я, 15-я и 20-я. На круге – 48.
2. По обе стороны каждой сильной точки – две слабые точки. На круге – 96.
3. В середине первой и третьей декады каждого Знака отмечаем по три слабые точки. На круге – 72.
4. Во второй декаде каждого Знака остается интервал, который соответствует четырем слабым долям – 12 по 4. На круге – 48.
5. В первой и третьей декаде остается по четыре слабых интервала – 24 по 4. На круге – 96.
Итого, мы должны отметить сильные доли – 48, слабые доли – 312. Всего – 360 долей.

Это означает, что разделив круг на 360 долей, можно наиболее полно определить энергетику круга, определить уровень сильных и слабых точек. Если мы захотим любое другое количество долей, то можем напрочь потерять всю информацию о круге.
Круг может иметь любой размер в сантиметрах или триллионах километрах, но у него всегда одна дистанция – 360° или 360 долей. Соответственно каждая доля в метрах у разных кругов будет отличаться. Но любой круг будет всегда ранжирован по уровню энергетики одинаково согласно положению градусов. Число 360 отмечает не просто количество, а качество, физику дистанции круга. Сделаем проекцию прямой линии на круг и узнаем энергетику прямой.

Поскольку для ученых круг это просто бублик, то градусы им нужны лишь как указатели направлений, вроде румбов. Иногда по кругу они гоняют частицы, потому что больше негде. А между тем, математика круга должна иметь неоценимое значение для физики, прежде всего квантовой. Представим себе Точку в начале времен. Это +-ноль, и там всё обнуляется, нет дистанции. Но вот появляется дистанция, и Точка принимает размеры Вселенной. Большая перемена, но это всего лишь Большая Точка. Помимо плюс размерности появляется минус размерность. А, значит, сохраняются отношения соединения с любой точкой круга. Поскольку за счет минус размерности Адреса аспектов прописаны моментально, то любая точка знает информацию о другой точке.

Видео:Почему в окружности именно 360 градусов?Скачать

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Числовая и единичная окружность

В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.

Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.

Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:

Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.

Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.

Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:

В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.

Выглядит единичная окружность так:

Видео:Что такое радиан | Почему в круге 360 | Профильный ЕГЭ математикаСкачать

Откладывание углов на единичной окружности

Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:

Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.

Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:

Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:

Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:

В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.

Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:

Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:

Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:

Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.

Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:

С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:

Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:

Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:

Например, верны следующие равенства:

15° + 3•360° = 15° + 1080° = 1095°

100° + 10•360° = 100° + 3600° = 3700°

1000° = 1000° – 2•360° = 1000° – 720° = 280°

Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5