Образом треугольника при движении является (7 видео)

Докажите, что при движении треугольник отображается на равный ему треугольник.

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
Понятие движения
Отображение плоскости на себя
Понятие движения
Теоремы, связанные с понятием движения
Готовые работы на аналогичную тему
Пример задачи на понятие движения
§ 1. Понятие движения
Отображение плоскости на себя
Понятие движения
Наложения и движения
Задачи
Ответы к задачам
📸 Видео

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Ваш ответ

Видео:9 класс, 30 урок, Понятие движенияСкачать

решение вопроса

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Понятие движения

Вы будете перенаправлены на Автор24

Видео:Отображение плоскости на себя. Понятие движения. Наложения и движенияСкачать

Отображение плоскости на себя

Отображение плоскости на себя — это такое соответствие каждой точке плоскости какой-либо точки этой же плоскости, при котором каждая точка плоскость будет сопоставленной для какой-либо точки.

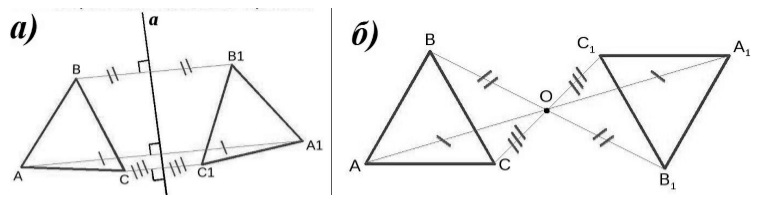
Примерами отображения плоскости на себя могут являться осевая симметрия (рис. 1,а) и центральная симметрия (рис. 1,б).

Рисунок 1. а) осевая симметрия; б) центральная симметрия

Видео:ДВИЖЕНИЕ 9 класс геометрия АтанасянСкачать

Понятие движения

Введем теперь определение движения.

Движением плоскости называется такое отображение плоскости на себя, при котором сохраняются расстояния (рис. 2).

Рисунок 2. Пример движения

Видео:Геометрия 9 класс (Урок№28 - Отображение плоскости на себя. Понятие движения. Наложения и движения.)Скачать

Теоремы, связанные с понятием движения

При движении отрезок отображается на равный ему отрезок.

Доказательство.

Пусть нам дан отрезок $MN$. Пусть при заданном движении плоскости точка $M$ отображается на точку $M_1$ этой плоскости, а точка $N$ отображается на точку $N_1$ этой плоскости. Возьмем произвольную точку $P$ отрезка $MN$. Пусть она отображается в точку $ P_1$ этой плоскости (рис. 3).

Рисунок 3. Отображение отрезка на отрезок при движении

Готовые работы на аналогичную тему

Так как точка $P$ принадлежит отрезку $MN$, то выполняется равенство

Так как, по определению движения, расстояния сохраняются, то

Значит, точка $P_1$ лежит на отрезке $M_1N_1$. В силу произвольности выбора точки $P_1$ получаем, что отрезок $MN$ при движении отобразится на отрезок $M_1N_1$. Равенство же этих отрезков сразу вытекает из определения движения.

Теорема доказана.

При движении треугольник отображается на равный треугольник.

Доказательство.

Пусть нам дан треугольник $ABC$. По теореме 1, отрезок $AB$ переходит в отрезок $A_1B_1$, отрезок $AC$ переходит в отрезок $A_1C_1$, отрезок $BC$ переходит в отрезок $B_1C_1$, причем $_1B_1$, $_1C_1$, $_1C_1$. Следовательно, по III признаку равенства треугольников, треугольник $ABC$ переходит в равный ему треугольник $A_1B_1C_1$.

Теорема доказана.

Аналогично можно доказать, что луч отображается на луч, угол отображается на равный ему угол.

Для формулирования следующей теоремы вначале ведем следующее определение.

Наложением называется такое движение плоскости, которое обладает следующими аксиомами:

Если при движении совпадают концы двух отрезков, то совпадают и сами отрезки.
От начала любого луча можно отложить отрезок, равный данному отрезку и притом только один.
В любую полуплоскость от любого луча можно отложить угол, равный данному неразвернутому углу, причем только один.
Любая фигура является равной самой себе.
Если фигура 1 равна фигуре 2, то и фигура 2 равна фигуре 1.
Если фигура 1 равна фигуре 2, а фигура 2 равна фигуре 3, то фигура 1 равна фигуре 3.

Любое движение является наложением.

Доказательство.

Рассмотрим движение $g$ треугольника $ABC$. По теореме 2, при движении $g$ треугольник $ABC$ переход в равный ему треугольник $A_1B_1C_1$. По определению равных треугольников получаем, что существует наложение $f$, отображающее точки $A,B и C$ на точки $A_1,B_1 и C_1$, соответственно. Докажем, что $g$ совпадает с $f$.

Предположим противное, что $g$ не совпадает с $f$. Тогда существует по крайней мере одна точка $M$, которая при движении $g$ переходит в точку $M_1$, а при наложении $f$ — в точку $M_2$. Так как, при $f$ и $g$ сохраняются расстояния, то имеем

То есть точка $A_1$ равноудалена от точек $M_1$ и $M_2$. Аналогично получим, что точки $B_1 и C_1$ равноудалены от точек $M_1$ и $M_2$. Значит точки $A_1,B_1 и C_1$ лежат на прямой, перпендикулярной к отрезку $M_1M_2$ и проходящей через его центр. Это не возможно, так как точки $A_1,B_1 и C_1$ не лежат на одной прямой. Следовательно, движение $g$ совпадает с наложением $f$.

Теорема доказана.

Видео:9 класс, 32 урок, Параллельный переносСкачать

Пример задачи на понятие движения

Доказать, что при движении угол отображается на равный ему угол.

Доказательство.

Пусть нам дан угол $AOB$. Пусть при заданном движении точки $A, O и B$ отображаются на точки $A_1, O_1 и B_1$. По теореме 2 получаем, что треугольник $AOB$ отображается на треугольник $A_1O_1B_1$, причем эти треугольники равны между собой. Следовательно, $angle AOB=angle A_1O_1B_1$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15 04 2021

Видео:Модуль 2. Баллистика. Равноускоренное движение в плоскости.Скачать

§ 1. Понятие движения

Отображение плоскости на себя

Слово «движение» вам знакомо. Но в геометрии оно имеет особый смысл. Какой именно, об этом вы узнаете из данной главы. А пока отметим, что с помощью движений удаётся находить красивые решения многих геометрических задач. Примеры таких решений вы найдёте в этой главе.

Представим себе, что каждой точке плоскости сопоставляется (ставится в соответствие) какая-то точка этой же плоскости, причём любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя.

Фактически мы уже встречались с отображениями плоскости на себя — вспомним осевую симметрию (см. п. 48). Она даёт нам пример такого отображения. В самом деле, пусть а — ось симметрии (рис. 321). Возьмём произвольную точку М, не лежащую на прямой а, и построим симметричную ей точку М₁ относительно прямой а. Для этого нужно провести перпендикуляр МР к прямой а и отложить на прямой МР отрезок РМ₁, равный отрезку МР, так, как показано на рисунке 321. Точка М₁ и будет искомой. Если же точка М лежит на прямой а, то симметричная ей точка М₁ совпадает с точкой М. Мы видим, что с помощью осевой симметрии каждой точке М плоскости сопоставляется точка М, этой же плоскости. При этом любая точка М₁ оказывается сопоставленной некоторой точке М. Это ясно из рисунка 321.

Итак, осевая симметрия представляет собой отображение плоскости на себя.

Рассмотрим теперь центральную симметрию плоскости (см. п. 48). Пусть О — центр симметрии. Каждой точке М плоскости сопоставляется точка М₁, симметричная точке М относительно точки О (рис. 322). Попытайтесь самостоятельно убедиться в том, что центральная симметрия плоскости также представляет собой отображение плоскости на себя.

Понятие движения

Осевая симметрия обладает следующим важным свойством — это отображение плоскости на себя, которое сохраняет расстояния между точками.

Поясним, что это значит. Пусть М и N — какие-либо точки, а М₁ и N₁ — симметричные им точки относительно прямой а (рис. 323). Из точек N и N₁ проведём перпендикуляры NP и N₁P₁ к прямой ММ₁. Прямоугольные треугольники MNP и M₁N₁P₁ равны по двум катетам: МР = М₁Р₁ и NP = N₁P₁ (объясните, почему эти катеты равны). Поэтому гипотенузы MN и M₁N₁ также равны.

Следовательно, расстояние между точками М и N равно расстоянию между симметричными им точками М₁ и N₁. Другие случаи расположения точек М, N и М₁, N₁ рассмотрите самостоятельно и убедитесь в том, что и в этих случаях MN = M₁N₁ (рис. 324). Таким образом, осевая симметрия является отображением, которое сохраняет расстояния между точками. Любое отображение, обладающее этим свойством, называется движением (или перемещением).

Итак, движение плоскости — это отображение плоскости на себя, сохраняющее расстояния.

Почему отображение, сохраняющее расстояния, называют движением (или перемещением), можно пояснить на примере осевой симметрии. Её можно представить как поворот плоскости в пространстве на 180° вокруг оси а. На рисунке 325 показано, каким образом происходит такой поворот.

Отметим, что центральная симметрия плоскости также является движением (пользуясь рисунком 326, убедитесь в этом самостоятельно).

Докажем следующую теорему:

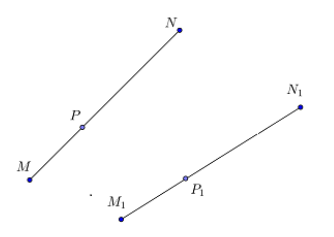
При движении отрезок отображается на отрезок.

Пусть при заданном движении плоскости концы М и N отрезка MN отображаются в точки М₁ и N₁ (рис. 327). Докажем, что весь отрезок MN отображается на отрезок M₁N₁. Пусть Р — произвольная точка отрезка MN, Р₁ — точка, в которую отображается точка Р. Тогда МР + PN = MN. Так как при движении расстояния сохраняются, то

Из равенств (1) получаем, что М₁Р₁ + P₁N₁ = M₁N₁, и, значит, точка Р₁ лежит на отрезке M₁N₁ (если предположить, что это не так, то будет выполняться неравенство М₁Р₁ +P₁N₁ > M₁N₁). Итак, точки отрезка MN отображаются в точки отрезка M₁N₁.

Нужно ещё доказать, что в каждую точку Р₁ отрезка M₁N₁ отображается какая-нибудь точка Р отрезка MN. Докажем это. Пусть Р₁ — произвольная точка отрезка M₁N₁, и точка Р при заданном движении отображается в точку Р₁. Из соотношений (1) и равенства M₁N₁ = М₁Р₁ + P₁N₁ следует, что МР + PN = MN, и, значит, точка Р лежит на отрезке MN. Теорема доказана.

При движении треугольник отображается на равный ему треугольник.

В самом деле, в силу доказанной теоремы при движении каждая сторона треугольника отображается на равный ей отрезок, поэтому и треугольник отображается на треугольник с соответственно равными сторонами, т. е. на равный треугольник.

Пользуясь доказанной теоремой, нетрудно убедиться в том, что при движении прямая отображается на прямую, луч — на луч, а угол — на равный ему угол.

Наложения и движения

Напомним, что в нашем курсе геометрии равенство фигур определяется с помощью наложений. Мы говорим, что фигура Ф равна фигуре Фп если фигуру Ф можно совместить наложением с фигурой Ф₁. Понятие наложения в нашем курсе относится к основным понятиям геометрии, поэтому определение наложения не даётся. Под наложением фигуры Ф на фигуру Ф₁ мы понимаем некоторое отображение фигуры Ф на фигуру Ф₁ Более того, мы считаем, что при этом не только точки фигуры Ф, но и любая точка плоскости отображается в определённую точку плоскости, т. е. наложение — это отображение плоскости на себя.

Однако не всякое отображение плоскости на себя мы называем наложением. Наложения — это такие отображения плоскости на себя, которые обладают свойствами, выраженными в аксиомах (см. приложение 1, аксиомы 7—13). Эти аксиомы позволяют доказать все те свойства наложений, которые мы себе представляем наглядно и которыми пользуемся при доказательстве теорем и решении задач. Докажем, например, что при наложении различные точки отображаются в различные точки.

В самом деле, предположим, что это не так, т. е. при некотором наложении какие-то две точки А и В отображаются в одну и ту же точку С. Тогда фигура Ф₁, состоящая из точек А и В, равна фигуре Ф₂, состоящей из одной точки С. Отсюда следует, что Ф₂ = Ф₁ (аксиома 12), т. е. при некотором наложении фигура Ф₂ отображается в фигуру Ф₁. Но это невозможно, так как наложение — это отображение, а при любом отображении точке С ставится в соответствие только одна точка плоскости.

Из доказанного утверждения следует, что при наложении отрезок отображается на равный ему отрезок. Действительно, пусть при наложении концы А и В отрезка АВ отображаются в точки А₁ и В₁. Тогда отрезок АВ отображается на отрезок А₁В₁ (аксиома 7), и, следовательно, отрезок АВ равен отрезку А₁В₁. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, сохраняющим расстояния, т. е. любое наложение является движением плоскости.

Докажем, что верно и обратное утверждение.

Любое движение является наложением.

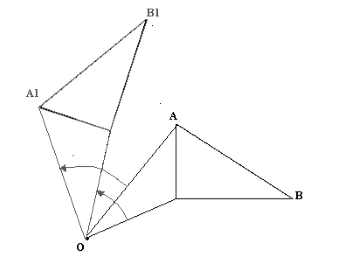
Рассмотрим произвольное движение (обозначим его буквой g) и докажем, что оно является наложением. Возьмём какой-нибудь треугольник АВС. При движении g он отображается на равный ему треугольник А₁В₁С₁. По определению равных треугольников существует наложение ƒ, при котором точки А, В и С отображаются соответственно в точки А₁, В₁ и С₁.

Докажем, что движение g совпадает с наложением ƒ. Предположим, что это не так. Тогда на плоскости найдётся хотя бы одна такая точка М, которая при движении g отображается в точку М„ а при наложении ƒ — в другую точку М2. Так как при отображениях ƒ u g сохраняются расстояния, то AM = А₁М₁, AM = А₁М₂, поэтому A₁M₁ = А₁М₂, т. е. точка А₁ равноудалена от точек М₁ и М₂ (рис. 328). Аналогично доказывается, что точки В₁ и С₁ равноудалены от точек М₁ и М₂. Отсюда следует, что точки А₁, В₁ и С₁ лежат на серединном перпендикуляре к отрезку М₁М₂. Но это невозможно, так как вершины треугольника А₁В₁С₁ не лежат на одной прямой. Таким образом, отображения ƒ u g совпадают, т. е. движение g является наложением. Теорема доказана.

При движении любая фигура отображается на равную ей фигуру.

Задачи

1148. Докажите, что при осевой симметрии плоскости:

а) прямая, параллельная оси симметрии, отображается на прямую, параллельную оси симметрии;
б) прямая, перпендикулярная к оси симметрии, отображается на себя.

1149. Докажите, что при центральной симметрии плоскости:

а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую;
б) прямая, проходящая через центр симметрии, отображается на себя.

1150. Докажите, что при движении угол отображается на равный ему угол.

Пусть при данном движении угол АОВ отображается на угол A₁O₁B₁, причём точки А, О, В отображаются соответственно в точки A₁, О₁, В₁. Так как при движении сохраняются расстояния, то ОА = О₁А₁, ОВ = О₁В₁. Если угол АОВ неразвёрнутый, то треугольники АОВ и А₁О₁В₁ равны по трём сторонам, и, следовательно, ∠AOB = ∠A₁O₁B₁. Если угол АОВ развёрнутый, то и угол А₁О₁В₁ развёрнутый (докажите это), поэтому эти углы равны.

1151. Докажите, что при движении параллельные прямые отображаются на параллельные прямые.

1152. Докажите, что при движении: а) параллелограмм отображается на параллелограмм; б) трапеция отображается на трапецию; в) ромб отображается на ромб; г) прямоугольник отображается на прямоугольник, а квадрат — на квадрат.

1153. Докажите, что при движении окружность отображается на окружность того же радиуса.

1154. Докажите, что отображение плоскости, при котором каждая точка отображается на себя, является наложением.

1155. АВС и А₁В₁С₁ — произвольные треугольники. Докажите, что существует не более одного движения, при котором точки А, В и С отображаются в точки А₁, В₁, С₁.

1156. В треугольниках АВС и А₁В₁С₁ АВ = А₁В₁, АС = А₁С₁, ВС = В₁С₁. Докажите, что существует движение, при котором точки А, В и С отображаются в точки А₁, В₁ и С₁, и притом только одно.

По условию задачи треугольники АВС и А₁В₁С₁ равны по трём сторонам. Следовательно, существует наложение, т. е. движение, при котором точки А, В и С отображаются соответственно в точки А₁, В₁ и С₁. Это движение является единственным движением, при котором точки А, В и С отображаются соответственно в точки А₁, В₁ и C₁ (задача 1155).

1157. Докажите, что два параллелограмма равны, если смежные стороны и угол между ними одного параллелограмма соответственно равны смежным сторонам и углу между ними другого параллелограмма.

1158. Даны две прямые а и b. Постройте прямую, на которую отображается прямая b при осевой симметрии с осью а.

1159. Даны прямая а и четырёхугольник ABCD. Постройте фигуру F, на которую отображается данный четырёхугольник при осевой симметрии с осью а. Что представляет собой фигура F?

1160 Даны точка О и прямая b. Постройте прямую, на которую отображается прямая b при центральной симметрии с центром О.

1161 Даны точка О и треугольник АВС. Постройте фигуру F, на которую отображается треугольник АВС при центральной симметрии с центром О. Что представляет собой фигура F?