Объем тетраэдра площадь треугольника (5 видео)

Объем тетраэдра

Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC .
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.

Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

S – площадь любой грани,
H – высота, опущенная на эту грань

Содержание

Правильный тетраэдр – частный вид тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Нахождение объема тетраэдра: формула и задачи
Формула вычисления объема тетраэдра
1. Общая формула (через площадь основания и высоту)
2. Объем правильного тетраэдра
Примеры задач
Объем тетраэдра площадь треугольника
📺 Видео

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

Все грани равны.
Все плоские углы правильного тетраэдра равны 60°
Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим

Применим формулу разность квадратов

После небольших преобразований получим

Объем любого тетраэдра можно рассчитать по формуле
,
где ,

Подставив эти значения, получим

Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра

Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

Видео:Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать

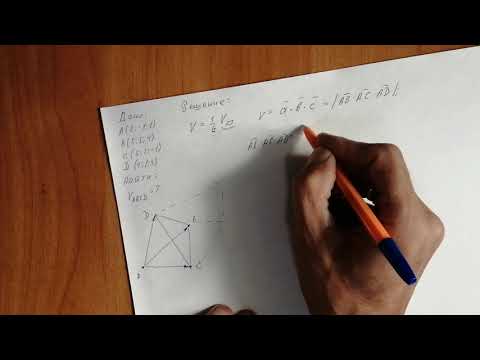
Нахождение объема тетраэдра: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем тетраэдра и разберем примеры решения задач для закрепления материала.

Видео:Задача 6. Вычислить объём тетраэдра с вершинами в точках и его высоту, опущенную из вершины на граньСкачать

Формула вычисления объема тетраэдра

1. Общая формула (через площадь основания и высоту)

Объем (V) тетраэдра считается также, как и объем любой пирамиды. Он равняется одной третьей произведения площади любой грани и высоты, опущенной на нее:

2. Объем правильного тетраэдра

В правильном тетраэдре все грани являются равносторонними треугольниками. Объем данной фигуры равен одной двенадцатой произведения длины его ребра в кубе на квадратный корень из числа 2.

Т.к. это правильный тетраэдр, все его ребра равны (AB = BC = AC = AD = BD = CD).

Видео:11 класс. Геометрия. Объём пирамиды. 28.04.2020.Скачать

Примеры задач

Задание 1
Площадь одной из граней тетраэдра равна 24 см 2 , а высоту, опущенная на нее – 9 см. Найдите объем фигуры.

Решение:
Применим общую формулу и получаем:

Задание 2
Дан правильный тетраэдр, ребро которого равняется 8 см. Найдите его объем.

Решение:
Воспользуемся формулой для расчета объема правильной фигуры:

Видео:Как вычислить расстояние между скрещивающимися прямыми через объем тетраэдра? Метод объемов 2Скачать

Объем тетраэдра площадь треугольника

Из основной формулы для объёма тетраэдра

(1),

где S – площадь любой грани, а H – опущенная на нее высота, можно вывести еще целый ряд формул, выражающих объём через различные элементы тетраэдра. Приведем эти формулы для тетраэдра ABCD.

(2) ,

где ∠ (AD,ABC) – угол между ребром AD и плоскостью грани ABC;

(3) ,

где ∠ (ABC,ABD) – угол между гранями ABC и ABD;

(4) ,

где |AB,CD| – расстояние между противоположными ребрами AB и CD, ∠ (AB,CD) – угол между этими ребрами.

Формулы (2)–(4) можно использовать для нахождения величин углов между прямыми и плоскостями; особенно полезна формула (4), с помощью которой можно находить расстояние между скрещивающимися прямыми AB иCD.

Формулы (2) и (3) аналогичны формуле S = (1/2)absin C для площади треугольника. Формуле S = rp аналогична формула

(5) ,

где r – радиус вписанной сферы тетраэдра, Σ – его полная поверхность (сумма площадей всех граней). Имеется и красивая формула, связывающая объём тетраэдра с радиусом R его описанной сферы (формула Крелле):

(6) ,

где Δ – площадь треугольника, стороны которого численно равны произведениям противоположных ребер (AB × CD, AC × BD,AD × BC). Из формулы (2) и теоремы косинусов для трехгранных углов (см. Сферическая тригонометрия) можно вывести формулу, аналогичную формуле Герона для треугольников:

(7) ,