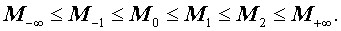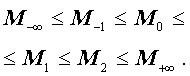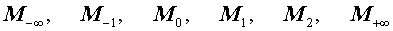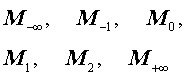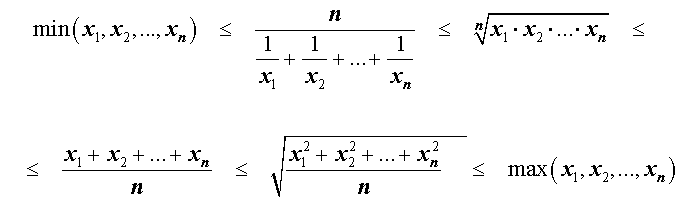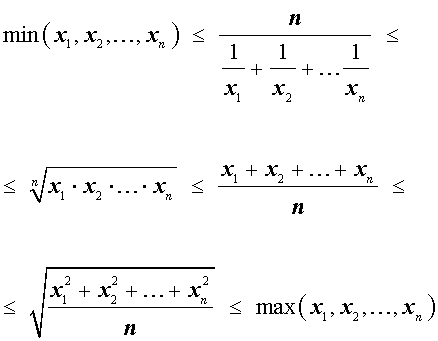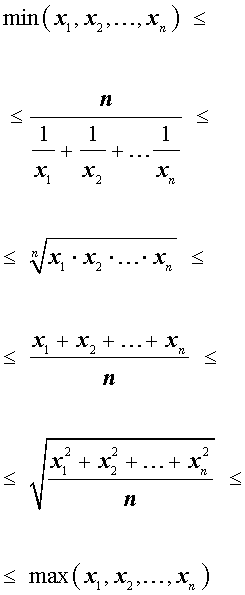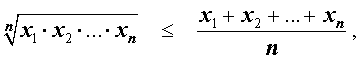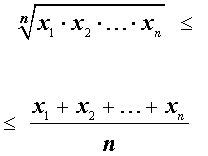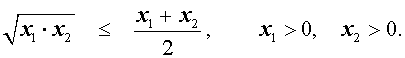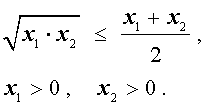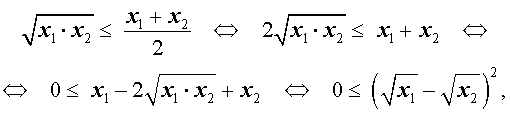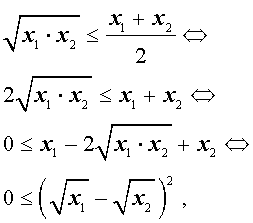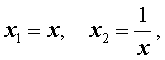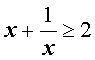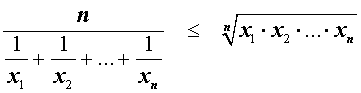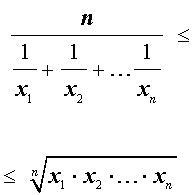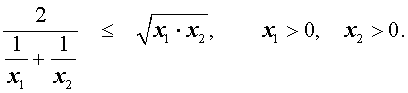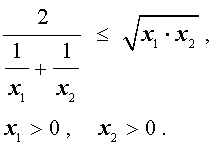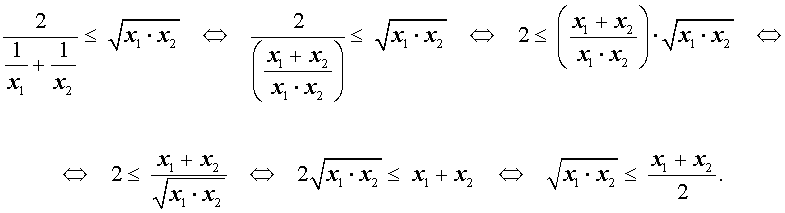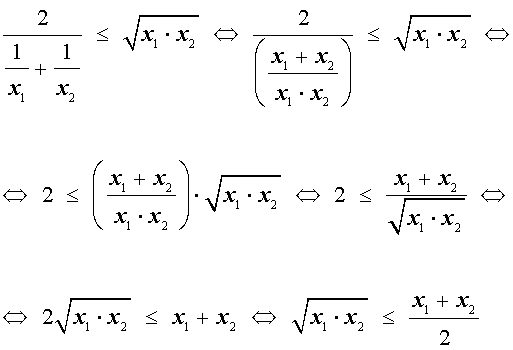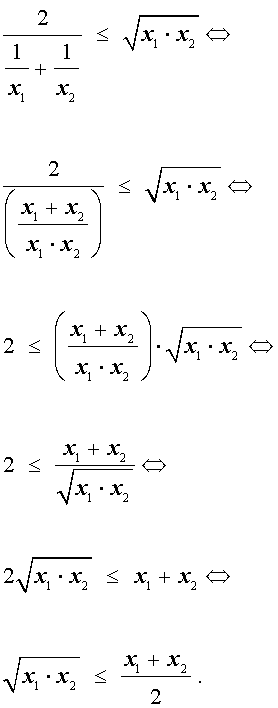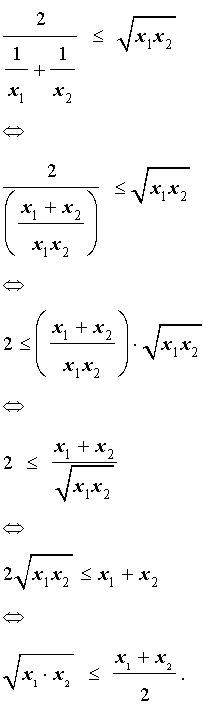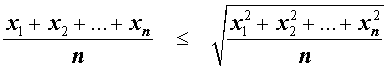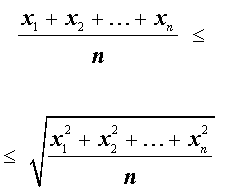Неравенства о средних в окружности

Неравенства между средними значениями

Неравенство Коши о среднем арифметическом и среднем геометрическом

Неравенство о среднем гармоническом и среднем геометрическом

Неравенство о среднем квадратичном и среднем арифметическом

Неравенства между средними значениями

Для удобства приведем Таблицу из введенных в разделе «Средние значения» определений средних значений для произвольного набора из n положительных действительных чисел

Таблица – Средние значения

Обозначение	Формула	Название
	min ( x1 , x2 , … , xn )	Минимум
M– 1		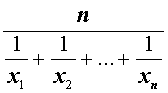Среднее гармоническое
M0		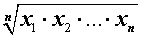Среднее геометрическое
M1		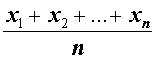Среднее арифметическое
M2		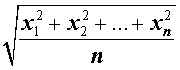Среднее квадратичное
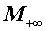	max ( x1 , x2 , … , xn )	Максимум

Среднее гармоническое

Среднее геометрическое

Среднее арифметическое

Среднее квадратичное

Утверждение 1 . Пусть p₁ и p₂ – произвольные действительные числа, удовлетворяющие неравенству p₁ Тогда для произвольного набора из n положительных действительных чисел

,

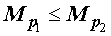
причем в этом неравенстве знак равенства выполняется тогда и только тогда, когда все числа

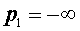
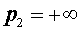
Замечание . Утверждение 1 остается справедливым и в случае, когда , и в случае, когда.

Следствие 1 . Для произвольного набора из n положительных чисел

справедливы следующие неравенства между его средними значениями:

Следствие 2 . Для произвольного набора из n положительных чисел

любые два из его средних значений

равны между собой тогда и только тогда, когда все числа

Итак, для n произвольных положительных чисел

справедлива следующая цепочка неравенств:

Неравенство Коши о среднем арифметическом и среднем геометрическом

утверждающее, что среднее геометрическое n положительных чисел не превосходит их среднего арифметического, называется неравенством Коши .

В случае, когда n = 2 , неравенство Коши имеет вид

Докажем это неравенство:

что и требовалось.

Из неравенства Коши с n = 2 , взяв

нетрудно получить очень полезное следствие .

Следствие . Для произвольного положительного числа x выполнено неравенство

Неравенство о среднем гармоническом и среднем геометрическом

В случае n переменных неравенство о среднем гармоническом и среднем геометрическом имеет вид:

В случае, когда n = 2 , это неравенство имеет вид:

Докажем это неравенство:

На последнем этапе получилось неравенство Коши, доказанное в предыдущем разделе, следовательно, доказательство неравенства о среднем гармоническом и среднем геометрическом закончено.

Неравенство о среднем квадратичном и среднем арифметическом

В случае n переменных неравенство о среднем квадратичном и среднем арифметическом имеет вид:

В случае, когда n = 2 , это неравенство имеет вид:

Различные средние положительных. Неравенство Коши

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Соотношение между средними величинами.

Сравнение среднего арифметического и среднего геометрического.

Хорошо известно, что с двумя положительными числами а и в , связаны их среднее арифметическое и среднее геометрическое, причем (равенство выполняется только при а = в ). Алгебраическое доказательство этого неравенства чрезвычайно простое:

Применим формулу «квадрат разности»:

Прибавим к обеим частям неравенства 4ав :

Применим формулу «квадрат суммы»:

Разделим обе части неравенства на 4 :

;

Так как а и в – положительные по условию, то извлечём из обеих частей неравенства квадратный корень:

Получили искомое выражение.

Сравнение среднего арифметического и среднего квадратичного.

По определению неравенства если (а – в) ≥0, то а ≥ в, а если (а – в)≤0, то а ≤ в. Но для положительных а и в имеет место выражение: если ( а² — в²)≥0, то а ≥ в и наоборот .

Для доказательства рассмотрим разность

Значит по определению неравенства (при а≥0; b ≥0 ) разность квадратов отрицательна, то есть уменьшаемое меньше вычитаемого. Таким образом , причём равенство достигается только при a = b .

Сравнение среднего гармонического и среднего геометрического.

Докажем, что среднее гармоническое не больше среднего геометрического, то есть . Рассмотрим разность

При условии, что a и b положительны разность квадратов , то есть уменьшаемое меньше вычитаемого. Значит , причём равенство достигается лишь при a = b .

Таким образом мы доказали одно из важнейших неравенств, связанных со средними:

.

Сравнение среднего арифметического и среднего геометрического для двух положительных чисел a и b .

Дано: окр. (О;ОА); AD = a ; BD = b

Доказать:

АВ – диаметр, АВ = a + b и , следовательно, .

угол АСВ – вписанный

дуга АКВ = 180° значит, угол АСВ = 90 ° (по свойству вписанного угла)

Таким образом, ∆АСВ – прямоугольный,

∆ АВС подобен ∆ ADC

(по общему острому углу)

2) ∆АВС подобен ∆ CBD

3) CD ┴АВ , то есть ∆ ADC подобен ∆ CBD .

4) , следовательно,

, следовательно,

, следовательно, , значит, , то есть .

5) ∆ CDO – прямоугольный, CD ┴ OD , значит, CD OC , то есть .

6) Если a = b , то точка D совпадает с точкой О , то .

Поэтому , что и требовалось доказать.

Это неравенство можно доказать и другим способом.

Дано: ABCD – прямоугольный, AD = a, AB = b, AK – биссектриса угла ВАD.

Доказать:

АК – биссектриса, следовательно, ВАL = LAD. LAD и BLA – внутренние накрест лежащие углы при параллельных ВС и AD и секущей AL, то есть BLA = LAD.

В = 90°, следовательно, BAL = LAD = 45°, но BLA = LAD, значит, ∆ АВL – равнобедренный, BL = AB = b.

∆ AKD – равнобедренный, так как KD ┴ AD, DAL = 45°, значит AD = KD = a.

4)

Очевидно, что , равенство достигается при

a = b , то есть ABCD – квадрат.

; ,

заменим в неравенстве а² на m , b ² на n , получим

или ,

то есть среднее геометрическое не больше среднего арифметического.

Сравнение среднего квадратичного и среднего арифметического.

Средние для n положительных чисел .

Средние величины можно находить для любого количества положительных чисел . Определения этих средних даны выше. Для любых положительных чисел среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее квадратичное удовлетворят неравенствам:

,

в каждом из которых знак равенства достигается лишь в случае, когда .

Самым важным и значимым из этих неравенств является неравенство о среднем арифметическом и среднем геометрическом, которое носит название неравенства Коши.

Замечательные пределы, порождаемые классическими средними.

Пусть даны два положительных числа a и b , a b . Вычислив какую – либо пару средних этих чисел, получим числа и . Затем для чисел и вычислим те же средние – получим числа и . С ними повторим ту же процедуру и так далее. В результате получим последовательности и .

Например, взяв среднее геометрическое и среднее арифметическое и отправляясь от чисел 1 и 3, получаем

В этом примере последовательности и очень быстро сближаются. Всегда ли так будет? Оказывается, подобные последовательности всегда имеют общий предел.

Арифметико – гармоническое среднее.

Пусть выбранная пара средних – это среднее гармоническое и среднее арифметическое; таким образом, члены последовательностей и определяются формулами

, , , .

Рассмотрим среднее гармоническое, среднее геометрическое и среднее арифметическое

.

Отсюда следует, что

.

То есть последовательность возрастает «навстречу» убывающей последовательности .

Таким образом, обе последовательности монотонны и ограничены, следовательно, они имеют пределы. Пусть , . Вычислим предел

То есть последовательности и имеют общий предел. Этот предел называется арифметико – гармоническим средним чисел a и b .

Так как и , где n =0, 1, 2, 3,… ; ; , то

, поэтому

Поэтому .

Арифметико – гармоническое среднее совпадает со средним геометрическим.

Таким образом последовательности и достаточно быстро сходятся к . Поэтому они могут оказаться полезными для приближённого вычисления квадратных корней. Для вычисления нужно начинать последовательности , с таких чисел a и b , что c = ab (например, a =1, b = c ), причём процесс будет сходиться тем быстрее, чем меньше разность между этими множителями (например, для вычисления лучше брать не a =1, b =56 , а a =7, b =8 ). Последовательности и получаются по формулам

; .

Для иллюстрации вычислим , положив b =4 . Получаем

и далее все знаки стабилизируются:

.

Арифметико – геометрическое среднее.

Четырнадцатилетний карл Фридрих Гаусс обнаружил на числовых примерах, что при вычислении последовательностей и с помощью арифметических и геометрических средних:

, ,

эти последовательности очень быстро сближаются.

Их общий предел называется арифметико – геометрическим средним чисел a и b и обозначается через . Найти явное выражение через a и b очень не просто. Впервые оно было получено Гауссом в результате необычайно остроумных и виртуозных рассуждений и преобразований, использующих свойства так называемых эллиптических интегралов.

Геометрическо – гармоническое среднее.

Если строить последовательности и с помощью средних гармонических и средних геометрических:

; ,

то в этом случае они сходятся к общему пределу. Назовём его геометрическо – гармоническим средним a и b и обозначим его через . Однако ничего существенно нового по сравнению с предыдущими последовательностями здесь нет, так как

; .

.

Неравенство круга

Решите систему неравенств

Решение:

Данную систему можно записать следующим образом:

Первое неравенство системы задает круг радиуса 5 с центром в точке А(2; -1), второе неравенство — круг радиуса 5 с центром в точке В(-4; 7) (смотри рисунок). Расстояние между центрами этих кругов равно

и, следовательно, равно сумме их радиусов. Значит, круги касаются и координаты точки касания С — единственное решение данной системы неравенств. Точка касания С является серединой отрезка АВ, и ее координаты можно найти как среднее арифметическое соответствующих координат точек А и В, то есть С(-1; 3).

Иные задачи с уравнениями и неравенствами кругов и окружностей здесь.

💥 Видео