Найти все числа t которым на числовой окружности соответствуют

№ 4.19 Найдите все числа t, которым на числовой окружности соответствуют точки, принадлежащие указанной открытой дуге (т.е. дуге без ее концов): а) АМ; б) СМ; в) МА; г) МС. (М – середина первой четверти). М.

Слайд 27 из презентации «Числовая единичная окружность (повторение)»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Числовая единичная окружность (повторение).pptx» можно в zip-архиве размером 1610 КБ.

Видео:Соответствие чисел точкам числовой окружностиСкачать

Похожие презентации

«Окружность 9 класс» — Уравнение окружности. Дано: М (-3; 4) – центр окружности О (0; 0) – точка на окружности. № 2 Вывести уравнение окружности с центром в точке М (-3; 4), проходящей через начало координат. № 1 Заполнить таблицу по следующим данным: Решить. О (хо, уо) – центр окружности, А (х; у) – точка окружности. Пусть d – расстояние от центра окружности до заданной точки плоскости, R – радиус окружности.

«Числовые последовательности» — Числовые последовательности. Геометрическая прогрессия. Способы задания. Арифметическая прогрессия. «Числовые последовательности». Урок-конференция.

«Предел числовой последовательности» — Числовые последовательности. Пример: 1, 4, 9, 16, …, п2, … — ограничена снизу 1. Последовательность простых чисел: 2; 3; 5; 7; 11; 13; 17; 19; 23; 29; … Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся. Возрастание и убывание числовой последовательности. Предел частного равен частному пределов:

«Числовые неравенства 8 класс» — Применение свойств числовых неравенств. Если a и b — неотрицательные числа и a>b, то a*n>b*n, где n — любое натуральное число. Если а>b и m>0, то am>bm. Оцените значение выражения. Если a>b, то a+c>b+c. Докажите, что функция y=x+3x возрастает. А>0 означает, что а – положительное число;

«Длина окружности» — ?? 3,14. Архимед. В Древнем Египте считали, что ??3,16. С=?d, C=2?r. Древний Рим. Великий ученый Древней Греции Архимед. R – радиус окружности. В Древнем Риме считали, что ?? 3,12. Древний Египет. Обозначения. Практическая работа «Измерение кофейных банок». Окружность. Великий математик Эйлер. D – диаметр окружности.

«Числовые неравенства» — Если a>b и m>0, то am>bm; Решение линейных неравенств. Если a>b и b>c , то a>c. Оглавление. Свойства числовых неравенств. Каждое такое значение переменной называют обычно решением неравенства с переменной. Свойство 4. Да мы сами уже могли убедиться в необходимости умения работать с неравенствами.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Числовая окружность

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac, frac, frac, 10π, -frac)) разбирается в этой статье .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки — положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);

4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:

Длина числовой окружности равна (2π) или примерно (6,28).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.

Видео:Точки на числовой окружностиСкачать

Какие точки соответствуют числам (1), (2) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac),(-frac),(frac), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Видео:Числовая окружность | Алгебра 10 класс #8 | ИнфоурокСкачать

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .

В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .

Что надо запомнить про числовую окружность:

Видео:№ 4.19- Алгебра 10-11 класс МордковичСкачать

Конспект урока :»Числовая окружность на координатной плоскости» (10 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Дисциплина: Алгебра и начала анализа

Тема: Числовая окружность на координатной плоскости

Цель урока: Рассмотреть окружность на координатной плоскости

— ввести понятие числовой окружности на координатной плоскости;

-сформулировать умения записывать множество чисел, соответствующих на числовой окружности точке;

-закрепить умение находить на числовой окружности точку, соответствующую данному числу;

— воспитание мотивов учения, положительного отношения к занятиям

— развитие умений применять теоретические знания на практике ;

— формирование познавательной потребности

Тип урока: Урок изучения и первичного закрепления новых знаний

I. Организационный момент

II. Актуализация учебной деятельности учащихся

III. Изучение нового материала

IV. Закрепление изученного материала

V. Подведение итогов урока

I. Организационный момент

а) сформулировать цели на данный урок

II. Актуализация учебной деятельности учащихся

1) проверить выполнение домашней работы (4 человека у доски)

3) провести самостоятельную работу по вариантам (приложение)

III. Изучение нового материала

Расположим числовую окружность в прямоугольной системе координат:

центр окружности совместим с началом координат.

Уравнение числовой окружности: x 2 +y 2 =1 (т.е R=1).

Начнем с первого рисунка числовой модели:

Рассмотрим прямоугольный треугольник ОРМ₁; ОМ₁ — это биссектрисаса, значит угол М₁ОР=45. ОМ₁=1(т.к это R), ОР=РМ₁; по теореме Пифагора найдем ОР; РМ₁=ОР=+-(корень из(2)/2).

В других четвертях будет меняться только знак.

Перейдем ко 2 рисунку числовой модели:

Рассмотрим прямоугольный треугольник ОРМ₁;радиус ОМ₁ делит прямой угол на три равных, значит угол М₁ОР=30; Катет лежащий напротив угла 30 градусов равен половине гипотенузы, значит РМ₁=1/2; по Теореме Пифагора х=+-(корень из(3)/2).

Аналогично проделайте сами с треугольником ОКМ₂.

Отметим все точки на числовой окружности:

IV. Закрепление изученного материала

V. Подведение итогов урока

Вариант 1 Ф.И. _______________________________________ Дата________________

1. Обозначьте на числовой окружности точки, которые соответствуют данным числам:

а) — p ; б) 5 p ; в) 5 p /6 ; г) — p /4 ; д) 7 p /3 ; е) — 3; ж) -55 p /6

2. Найдите все числа, которым соответствуют на числовой окружности точки A , M, S, C

3. Найдите все числа t , которым на числовой окружности соответствуют точки, принадлежащие заданной дуге:

а) ВС; б) СВ; в) PN ; г) DM

4. Укажите на числовой окружности дугу, точки которой удовлетворяют неравенству

Вариант 2 Ф.И._______________________________________Дата________________

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) -2 p ; б) 3 p ; в) 11 p /6 ; г) — 2 p /3 ; д) 3 p /4 ; е) — 2; ж) -35 p /4

2. Найдите все числа, которым соответствуют на числовой окружности точки B , N , L , D

3. Найдите все числа t , которым на числовой окружности соответствуют точки, принадлежащие заданной дуге:

а) С D ; б) D С; в) KL ; г) DP

4. Укажите на числовой окружности дугу, точки которой удовлетворяют неравенству

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) — p ; б) 5 p ; в) 5 p /6 ; г) — p /4 ; д) 7 p /3 ; е) — 3.

2. На числовой окружности укажите все точки, координаты которых удовлетворяют данным условиям, и составьте формулы для всех чисел, которым соответствуют эти точки:

а) б) в) г)

3. Найдите на числовой окружности точки, координаты которых удовлетворяют заданному неравенству и запишите каким числам t они удовлетворяют:

а) б)

4. Укажите на числовой окружности дугу, точки которой удовлетворяют неравенству

1. Обозначьте на числовой окружности точку, которая соответствует данному числу:

а) -2 p ; б) 3 p ; в) 11 p /6 ; г) — 2 p /3 ; д) 3 p /4 ; е) — 2.

2. На числовой окружности укажите все точки, координаты которых удовлетворяют данным условиям, и составьте формулы для всех чисел, которым соответствуют эти точки:

а) б) в) г)

3. Найдите на числовой окружности точки, координаты которых удовлетворяют заданному неравенству и запишите каким числам t они удовлетворяют:

а) б)

4. Укажите на числовой окружности дугу, точки которой удовлетворяют неравенству

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 986 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 312 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:№ 4.20- Алгебра 10-11 класс МордковичСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 532 411 материалов в базе

Материал подходит для УМК

«Алгебра и начала математического анализа (базовый и углубленный уровень) (в 2 частях), изд-во «Мнемозина»», Мордкович А.Г.

§ 12. Числовая окружность на координатной плоскости

Другие материалы

• 05.02.2021
• 108
• 1

• 05.02.2021
• 80
• 0

• 05.02.2021
• 112
• 0

• 05.02.2021
• 190
• 1

• 04.02.2021
• 155
• 8

• 04.02.2021
• 154
• 7

• 04.02.2021
• 65
• 0

• 04.02.2021
• 120
• 5

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 05.02.2021 1082
• DOCX 435 кбайт
• 163 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Сагарда Ирина Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 8 месяцев
• Подписчики: 0
• Всего просмотров: 12041
• Всего материалов: 12

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Как искать точки на тригонометрической окружности.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Тульской области ввели школьные каникулы со 2 по 11 февраля

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Томске из-за COVID-19 перенесут каникулы для первоклассников

Время чтения: 1 минута

В России планируют создадут сеть центров для подростков «группы риска»

Время чтения: 1 минута

В Курганской области школьников переведут на дистанционное обучение с 4 февраля

Время чтения: 1 минута

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📹 Видео

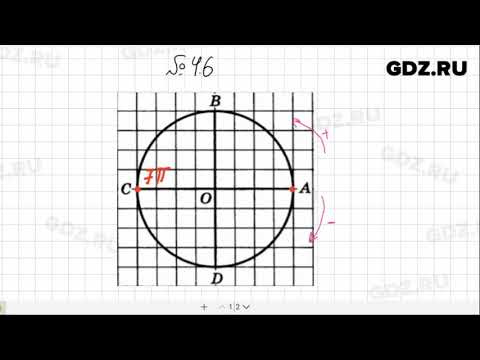
№ 4.6- Алгебра 10-11 класс МордковичСкачать

Как решить вторую часть на максимум? | Математика ОГЭ 2023 | УмскулСкачать

№ 4.11- Алгебра 10-11 класс МордковичСкачать

Математика 10 Класс (Алгебра и Геометрия)Скачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

№ 4.15- Алгебра 10-11 класс МордковичСкачать

№ 5.4- Алгебра 10-11 класс МордковичСкачать

Алгебра 10 класс. 15 сентября. Числовая окружность #1Скачать

№ 4.14- Алгебра 10-11 класс МордковичСкачать

Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Тригонометрия с нуля до ЕГЭ за 6 часов | Математика ЕГЭ 10 класс | УмскулСкачать

Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

Тригонометрическая окружность. Как выучить?Скачать