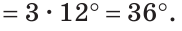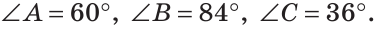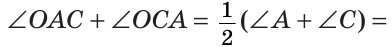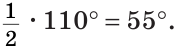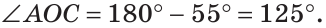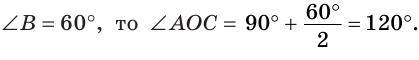Видео:№224. Найдите углы треугольника ABC, если ∠A:∠B:∠C= 2:3:4.Скачать

Ваш ответ
Видео:№ 136 - Геометрия 7-9 класс АтанасянСкачать

Похожие вопросы
- Все категории
- экономические 43,287
- гуманитарные 33,620
- юридические 17,900
- школьный раздел 607,113
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:№136. На рисунке 52 (с. 31) АВ =AC, BD = DC и ∠BAC = 50°. Найдите ∠CAD.Скачать

Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Видео:Задание № 136 — Геометрия 7 класс (Атанасян)Скачать

Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
 | (1) |
 | (2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 . . |
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
 . . |
 . . |
Далее, из формулы
 . . |
 . . | (3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 . . |
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
 , , |
   . . |
Из формулы (3) найдем cosA:
  |
 . . |
Поскольку уже нам известны два угла то находим третий:
  . . |
Видео:№ 136 - Геометрия 9 класс МерзлякСкачать

Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
 . . |
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
Видео:Задание №136 — ГДЗ по геометрии 10 класс (Атанасян Л.С.)Скачать

Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
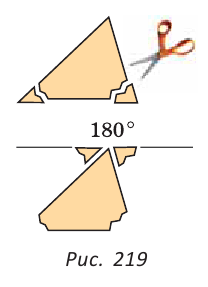
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
Доказательство:
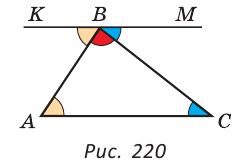
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 





Следствия.
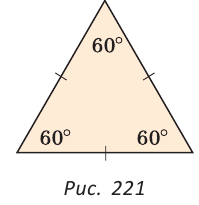
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
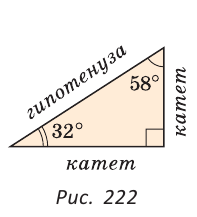
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
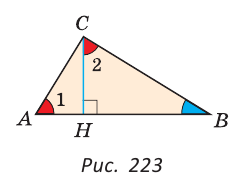
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
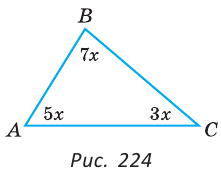
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 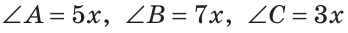
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
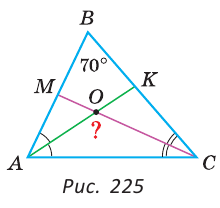
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 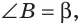
Пример:
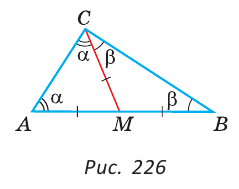
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 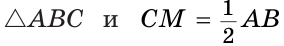
Докажем, что























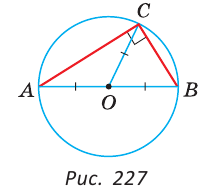
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
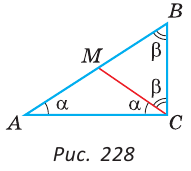
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎦 Видео
Задача 6 №27919 ЕГЭ по математике. Урок 136Скачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

№1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать

В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать

№ 136 - Геометрия 7 класс МерзлякСкачать

ГДЗ по геометрии / Номер 136, 137 Геометрия 7 класс Атанасян Л.С. / Подробный разборСкачать

§136 Значения тригонометрических функций для угла 45 градусовСкачать

№ 136- Геометрия 7-9 класс АтанасянСкачать

Внешний угол треугольникаСкачать

КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

№678. Биссектрисы АА1 и ВВ1 треугольника ABC пересекаются в точке М. Найдите углы ACM и ВСМ, если:Скачать