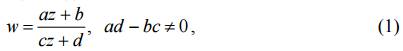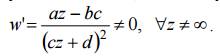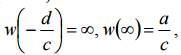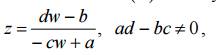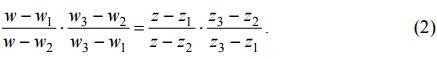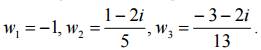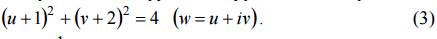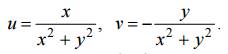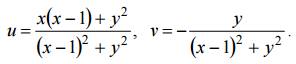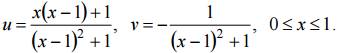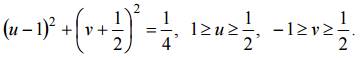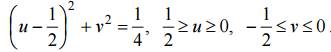Найти симметричный образ относительно единичной окружности (3 видео)

Конформные отображения. Дробно-линейная функция

Содержание

Конформные отображения. Дробно-линейная функция
Найти симметричный образ относительно единичной окружности
Сохранение симметрии при дробно-линейном отображении.
📹 Видео

Видео:Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать

Конформные отображения. Дробно-линейная функция

Определение 1. Функция вида

где a, b, c, d – комплексные числа, называется дробно-линейной.

Отображение, задаваемое этой функцией, называется дробно- линейным.

Условие ad − bc ≠ 0 означает, что w ≠ const . Функция (1) осуществляет конформное отображение расширенной комплексной плоскости Z на расширенную комплексную плоскость w, так как производная

Для 0 c ≠ предполагаем, что

для c = 0 функция (1) становится линейной, т. е. w = az + b и w(∞) = ∞. Функция

является обратной к функции (1). Она также является дробно-линейной и однозначной на расширенной комплексной плоскости, т. е. здесь функция (1) является однолистной.

Каждое дробно-линейное отображение может быть получено в результате последовательного выполнения трех отображений: линейного, отображения w = 1/z и снова линейного отображения.

Дробно-линейные отображения переводят:

1) окружность или прямую в окружность или прямую (круговое свойство);

2) пару точек, симметричных относительно окружности, – в пару то- чек, симметричных относительно образа этой окружности (свойство сохранения симметрии). Здесь «окружность», в частности, может быть прямой, если под последней понимать окружность бесконечного радиуса.

Существует единственное дробно-линейное отображение, которое три разных точки z₁, z₂, z₃ переводит соответственно в три разные точки w₁, w₂, w₃. Это отображение задается формулой

Если одна из точек z_k или w_k (k =1, 2, 3) является бесконечно удаленной точкой, то в формуле (2) разности, в которые входит z_k или w_k, требуется заменить единицами.

Существует бесконечно много дробно-линейных отображений, которые заданную окружность γ отображают на заданную окружность Г, причем область D, для которой γ является границей, отображается на одну из областей, для которой Г является границей.

Для обеспечения единственности дробно-линейного отображения достаточно выполнение одного из условий:

1) заданная точка z₀ ∈ D отображается в заданную точку w₀ ∈ D’, а любая кривая, выходящая из точки z₀, поворачивается на заданный угол α w₀ = f (z₀), α = arg(f ‘(z₀));

2) точки z₀ ∈ D и z₁ ∈ γ отображаются соответственно в заданные точки w₀ ∈ D’ и w₁ ∈ Γ.

Пример 1. Найти образ окружности, заданной уравнением

x 2 + y 2 + 2x − 4y + 1 = 0,

при отображении w = 1/z.

Решение. На основании кругового свойства дробно-линейного отображения окружность переходит в окружность. Для ее нахождения на заданной окружности x 2 + y 2 + 2x − 4y + 1 = 0, выберем три точки, например: z₁ = −1 z₂ = 1 + 2i, z₃ = −3 + 2i, образами которых при отображении w = 1/z будут точки

Точками w₁, w₂, w₃ однозначно определяется образ данной окружности, уравнение которой:

Для отображения w = 1/z имеем

Выразив отсюда x = x(u, v), y = (u, v) и подставив в уравнение заданной окружности, получим искомый образ (3).

Пример 2. Найти образ области D при отображении 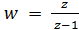, где D = <z, 0

Будем искать образ границы области D (рис. 1).

Сторона OA: y = 0, 0 ≤ x ≤ 1 отображается на отрицательную часть действительной оси (v = 0, − ∞

Рис. 1. Область D

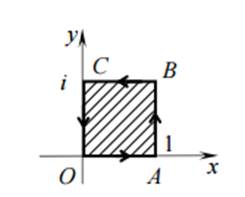
Рис. 2. Образ области D

Сторона AB: x = 1, 0

Сторона BC: y =1, 1 ≥ x ≥ 0, отображается в линию, параметрическое уравнение которой имеет вид

Исключив параметр x, получим

Аналогично образ стороны CO определяется уравнением

В соответствии с принципом соответствия границ образом квадрата будет заштрихованная область на рис. 1.

Пример 3. Найти дробно-линейное отображение, которое точки z₁ = 1 и z₂ = −1 оставляет неподвижными, а точку z₃ = i переводит в точку w₃ = 0.

Найти образ полуплоскости Im(z) > 0 при данном отображении.

Решение. По условию имеем три пары соответствующих точек

Применяя формулу (2), получим искомое дробно-линейное отображение .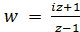

Найдем теперь образ верхней полуплоскости, границей которой является действительная ось. Согласно круговому свойству действительная ось отображается в окружность. Чтобы найти ее, на действительной оси выберем три точки, например: z₁ =1, z₂ = 0, z₃ = −1, образами которых бу- дут точки w₁ = 1, w₂ = −i, w₃ = −1. Они лежат на окружности |w| =1. По принципу соответствия границ получаем, что образом верхней полуплоскости будет область D’= <w, |w|

Пример 4. Найти дробно-линейное отображение, которое круг |z − 4i| u так, что w(4i) = −4, w(2i) = 0.

Решение. Условие задачи определяет две пары соответствующих точек. Третью пару найдем, пользуясь свойством симметрии дробно линейного отображения, согласно которому точки z₁ = 4i и z₃ = ∞, симметричные относительно окружности |z − 4i| = 2, перейдут в точки w₁ = −4 и w₃ = − 4i, симметричные относительно прямой u = v . Таким образом, найдена третья пара точек z₃ = ∞ и w₃ = −4i. По формуле (2) найдем искомое отображение .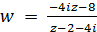

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Найти симметричный образ относительно единичной окружности

Название работы: Дробно-линейные отображения

Предметная область: Математика и математический анализ

Описание: Отображение инверсия преобразование симметрии относительно единичной окружности. Вообще точки и называют симметричными относительно окружности : если 1 они лежат на одном луче проходящем через точку 2 Преобразование переводящее каждую точку плоскости в точку симметричную относительно окружности называют симметрией относительно этой окружности или инверсией. Докажем основное свойство симметричных точек: Точки и тогда и только тогда являются симметричными относительно окружности когда они являются вершинами пучка.

Дата добавления: 2013-08-04

Размер файла: 824.5 KB

Работу скачали: 79 чел.

Дробно-линейными называют отображения, осуществляемые дробно-линейными функциями

где — комплексные постоянные, причем , т.к. иначе , т.е. функция (1) сводится к постоянной.

Функция (1) определена на полной плоскости (ее значение в точке считается равным , а в точке — равным ).

существует при всех , поэтому функция (1) аналитична в полной плоскости, кроме точки , где она имеет полюс I порядка. Уравнение (1) однозначно разрешимо относительно :

причем функция (3) также определена в полной плоскости (ее значение в точке считается равным , а в точке — равным ). Поэтому дробно-линейная функция осуществляет однолистное отображение полной плоскости на полную плоскость .

Легко видеть, что дробно-линейная функция единственная функция, обладающая этим свойством. Справедлива

Если функция всюду однолистна и аналитична всюду в полной плоскости , кроме точки , то она дробно-линейная.

Точка не может быть существенно особой, т.к. тогда по теореме Сохоцкого была бы заведомо неоднолистной. По теореме Лиувилля не может быть устранимой особой точкой. Следовательно, точка есть полюс, причем первого порядка, ибо в окрестности полюса высшего порядка функция опять-таки неоднолистна. Если , то главная часть в окрестности точки имеет вид . Функция не имеет особенностей в полной плоскости (единственной особой точкой для могла бы служить точка , но она является устранимой особой точкой, ибо мы вычли из главную часть). Следовательно, , и функция дробно-линейна. Если , то главная часть имеет вид , и точно также доказывается, что , т.е. является целой линейной функцией.

Формула (3) показывает, что функция обратная к дробно-линейной, снова дробно-линейна. Легко показать, что сложная функция, составленная из дробно-линейных функций, также является дробно-линейной.

Выясним геометрические свойства дробно-линейной функции.

Если , то функция (1) приводится к целой линейной функции, геометрические свойства которой были рассмотрены ранее. При представим функцию (1) в виде

(где — некоторые постоянные), поделив в (1) числитель на знаменатель. Будем рассматривать отображение (4) как сложное, составленное из отображений

Отображение (а) сводится к сдвигу, (в) к сдвигу и повороту с растяжением. Остается изучить отображение (б), которое запишем в виде

В полярных координатах , отображение (6) перепишется в виде

Удобно рассматривать отображение (7) как составленное из двух геометрически более наглядных отображений

Отображение есть преобразование симметрии относительно действительной оси. Отображение — инверсия , преобразование симметрии относительно единичной окружности.

Вообще точки и называют симметричными относительно окружности : , если

1) они лежат на одном луче, проходящем через точку,

Преобразование, переводящее каждую точку плоскости в точку , симметричную относительно окружности , называют симметрией относительно этой окружности или инверсией .

Докажем основное свойство симметричных точек :

Точки и тогда и только тогда являются симметричными относительно окружности , когда они являются вершинами пучка окружностей, ортогональных к окружности .

Пусть точки и симметричны относительно , — произвольная окружность, проходящая через и (см. рис.). Проведем через касательную к окружности. По известной теореме квадрат длины этой касательной равен произведению секущей на ее внешнюю часть , т.е. .

Так как и симметричны относительно , то , поэтому . Таким образом, касательная к является радиусом окружности , т.е. ортогональна к .

Обратно, если и являются вершинами пучка окружностей , ортогональных к окружности , то они лежат на луче, проходящем через , так как этот луч принадлежит пучку (в полной плоскости мы рассматриваем прямые как частный случай окружностей это окружности, проходящие через бесконечно удаленную точку). Далее, касательная к любой окружности является радиусом окружности и по той же теореме , т.е. и симметричны относительно . Ч.т.д.

Из этого свойства, в частности, вытекает, что в случае, когда окружность вырождается в прямую линию, симметрия относительно окружности превращается в обычную симметрию.

Инверсия относительно произвольной окружности является конформным отображением второго рода (меняющим ориентацию). В самом деле, пусть и — центр и радиус окружности , тогда точку , симметричную с точкой относительно , можно задать формулой

ибо отсюда следует, что , .

Следовательно, инверсия отличается от конформного отображения

лишь дополнительной симметрией относительно действительной оси плоскости , т.е. является конформным отображением второго рода.

Покажем, далее, что инверсия преобразует любую окружность полной плоскости снова в окружность ( круговое свойство ) .

В самом деле, пусть сначала окружность проходит через центр окружности , относительно которой производится инверсия (см. рис.). Построим прямую перпендикулярную к линии центров окружностей и , на расстоянии от ( и — радиусы и соответственно). Из подобия треугольников и имеем

Следовательно, точки и симметричны относительно . Мы доказали, что точка, симметричная к произвольной точке окружности , лежит на прямой , т.е. что является инверсией окружности . Если, в частности, есть прямая, проходящая через , то инверсия этой прямой, очевидно, совпадает с ней самой.

Пусть теперь окружность (или прямая) не проходит через . Построим точку , симметричную с относительно , и рассмотрим пучок окружностей с вершинами в и . Так как все окружности проходят через , то по доказанному выше при инверсии относительно пучок перейдет в пучок прямых . Вершина этого пучка будет, очевидно, лежать в точке , симметричной точке относительно . По свойству симметричных точек все окружности ортогональны к , и так как инверсия сохраняет углы (мы доказали выше, что она является конформным отображением второго рода), то образ окружности будет ортогонален пучку прямых. Отсюда следует, что является окружностью. Свойство доказано.

Точно так же доказывается еще одно свойство инверсии.

Инверсия преобразует любую пару точек и , симметричных относительно произвольной окружности , в пару точек и , симметричных относительно окружности — образа окружности ( свойство сохранения симметричных точек ) .

В самом деле, построим пучок окружностей с вершинами в и . При инверсии он перейдет в пучок окружностей с вершинами в и . Т.к. окружности ортогональны к , то и окружности ортогональны к . Отсюда следует, что и симметричны относительно . Свойство доказано.

Так как отображение составляется из двух симметрий (симметрии () относительно единичной окружности и симметрии () относительно прямой), то оно обладает круговым свойством и свойством сохранения симметричных точек. Так как остальные преобразования, составляющие произвольное дробно-линейное отображение (преобразования (а) и (в) из формулы (5), т.е. сдвиг и поворот с растяжением), очевидно, также обладают этими свойствами, то эти свойства остаются справедливыми и для произвольного дробно-линейного отображения.

Докажем, что произвольное дробно-линейное отображение (1) сохраняет углы в полной плоскости .

Это очевидно для всех точек , кроме и , ибо для всех таких точек существует (см. (2)). Для рассмотрения точек и нужно ввести понятие угла в бесконечно удаленной точке. Под углом в бесконечно удаленной точке между двумя прямыми понимают взятый с противоположным знаком угол во второй (конечной) точке пересечения этих прямых (на рисунке угол в бесконечности между прямыми I и II отрицателен).

Ясно, что отображения (а) и (в) сохраняют углы всюду. Отображение (в), т.е. отображение сохраняет углы, в том числе и в точках ; это непосредственно видно из рисунка и принятого нами определения (при отображение прямая переходит в прямую ).

Основные свойства дробно-линейного отображения, доказанные выше, могут быть сформулированы в виде следующей

Произвольная дробно-линейная функция , , осуществляет однолистное конформное отображение полной — плоскости на полную — плоскость. Это отображение

преобразует любую окружность полной — плоскости в окружность полной — плоскости (круговое свойство);
любую пару точек, симметричных относительно окружности , преобразует в пару точек, симметричных относительно образа окружности (свойство сохранения симметричных точек).

В заключение приведем формулы, по которым можно вычислять образы прямых и окружностей при произвольном дробно-линейном отображении (1):

Прямым , не проходящим через точку , соответствуют окружности , где , . (9)
Прямым , проходящим через точку , — прямые

Окружностям , не проходящим через точку , — окружности , где

Эти формулы можно получить непосредственным подсчетом.

Частные случаи дробно-линейного отображения.

Произвольное дробно-линейное преобразование можно переписать в виде

Мы считаем, что и .

Имеет место следующая

Заданием соответствия трем различным точкам плоскости трех различных точек плоскости дробно-линейная функция определена однозначно.

Мы должны доказать, что условия

где , , ; , , — заданные комплексные числа, однозначно определяют значения параметров , , .

Разделив (3) на (4), получим

Для произвольной точки имеем аналогичное соотношение

Исключая из (5) и (6) параметр , окончательно получим

Соотношение (7) и представляет собой неявное выражение искомой дробно-линейной функции. Разрешив (7) относительно, мы получим явные выражения коэффициентов , , дробно-линейной функции через заданные числа , , ;, , , что и доказывает теорему.

Из доказанной теоремы вытекает

Любой круг полной плоскости с помощью дробно-линейной функции можно преобразовать в любой круг полной — плоскости.

Действительно, пусть и — заданные круги, соответственно в плоскостях и, а и — их границы.

Выберем на три точки , занумерованные в порядке положительного обхода , и также три точки на . Если теперь по формуле (7) построить дробно-линейное отображение, то это отображение, согласно круговому свойству, будет переводить окружность в и, согласно принципу соответствия границ, круг — в один из двух кругов, ограниченных . Но, так как конформные отображения сохраняют ориентацию, и точки расположены относительно так же, как точки относительно , то преобразуется именно в . Ч.т.д.

Рассмотрим несколько примеров.

Отображение верхней полуплоскости на единичный круг.

Зададимся точкой верхней полуплоскости, переходящей в центр круга (см. рис.). По свойству сохранения сопряжен-ных точек точка , симметричная точке относительно действи-тельной оси, должна перейти в точку , симметричную точке относительно единичной окружности. Поэтому искомое отображение должно иметь вид

где . При любом эта функция отображает верхнюю полуплоскость на некоторый круг с центром в точке, так как точка должна быть симметричной точке относительно границы того круга. Подберем так, чтобы круг был единичным. Для этого достаточно потребовать, чтобы точка перешла в точку единичной окружности: . Таким образом, можно положить и нашу задачу решает функция

где — любое действительное число (изменение означает поворот круга относительно центра).

По свойствам дробно-линейного отображения пучку радиусов круга (т.е. дуг окружностей, проходящих через точки и) соответствуют дуги окружностей (принадлежащие верхней полуплоскости), проходящих через точки и . Семейству окружностей с центром в точке соответствуют окружности, имеющие и своими симметричными точками (см. рис.)

Укажем также обратное к (9) отображение единичного круга на верхнюю полуплоскость. Положим для упрощения , получим

Полагая здесь и умножая числитель и знаменатель на , находим соответствие между точками единичной окружности и оси , которое устанавливает отображение (10):

Отображение единичного круга на единичный круг.

Зададимся точкой круга , переходящей в центр круга . Точка , симметричная с относительно единичной окружности, должна переходить в точку. Следовательно, искомое отображение должно иметь вид

где . Подберем так, чтобы круг в плоскости был единичным. Для этого достаточно потребовать, чтобы точка перешла в точку единичной окружности: .

Таким образом, можно принять , т.е. нашу задачу решает функция

где — любое действительное число. Так как

и , то геометрически означает угол поворота отображения (11) в точке :

Растяжение отображения (11) в точке :

стремится к бесконечности, если точка стремится к границе единичного круга.

На рисунке указаны линии, соответствующие друг другу при этом отображении.

Если , (точки на соответствующих окружностях), то, полагая для упрощения , , , получим

(мы в формулу (11) подставили выражение для , , , умножили обе части на и отделили действительную часть).

Если радиус круга в плоскости равен , то функция , отображающая этот круг на круг при условиях , , имеет вид

Эта формула получается из (11) заменой на и соответственно на .

Видео:Лекция №13 по ТФКП. Функция Жуковского. Конформные отображения. Городецкий С.Е.Скачать

Сохранение симметрии при дробно-линейном отображении.

Замечание 2. Дробно-линейное отображение преобразует окружность в прямую, если проходит через точку , которая переходит в бесконечно удаленную точку. Если окружность не проходит через точку , то при указанном дробно-линейном отображении перейдет в окружность. Аналогичным образом преобразуются и прямые: прямая при отображении переходит в прямую, если проходит через точку . Иначе переходит в окружность.

Определение 5. Точки и называют симметричными относительно окружности в , если они лежат на одном луче, выходящем из центра окружности , и произведение их расстояний до центра окружности равно квадрату радиуса окружности, т.е. и .

Так как для точек и , симметричных относительно окружности , верно соотношение , то равно действительному положительному числу. А поскольку, согласно определению,

Так как при приближении точки к центру окружности симметричная ей точка стремится к бесконечно удаленной точке, то центр окружности и бесконечности удаленную точку естественно считать симметричными относительно окружности .

Теорема 11. Произвольное дробно-линейное отображение преобразует любые точки и , симметричные относительно окружности на , в точки и , симметричные относительно образа этой окружности.

Рассмотрим семейство всех окружностей на , проходящих через и . Каждая из этих окружностей перпендикулярна . Дробно-линейное отображение переводит каждую окружность в окружность в , перпендикулярную (в силу теоремы : Функция с дополнением и осуществляет взаимно однозначное и непрерывное отображение расширенной комплексной плоскости на расширенную коплексную плоскость ) образу окружности . Согласно критерию симметричности точек, получаем, что точки и , через которые проходят все окружности семейства , симметричны относительно окружности .