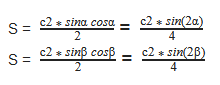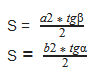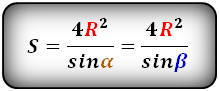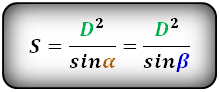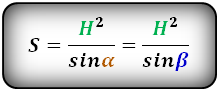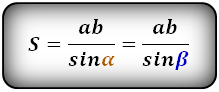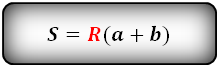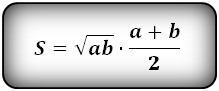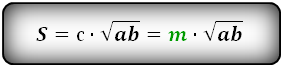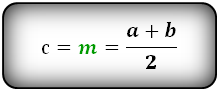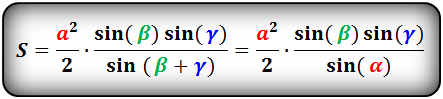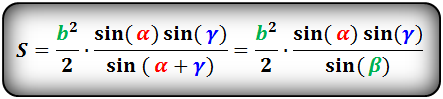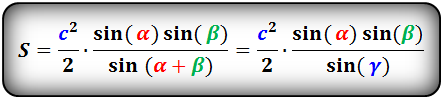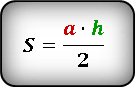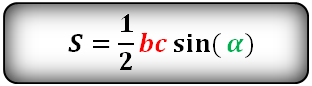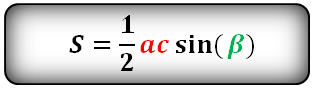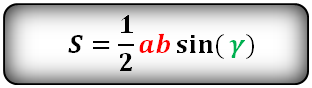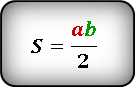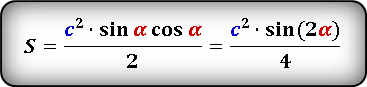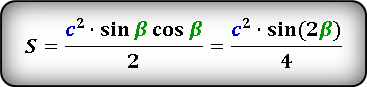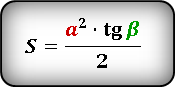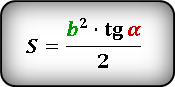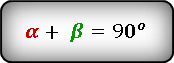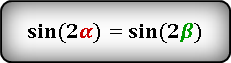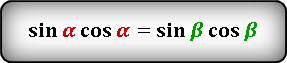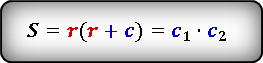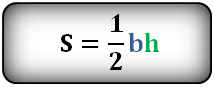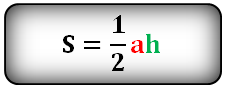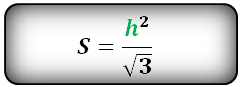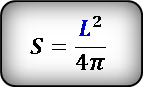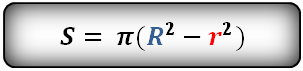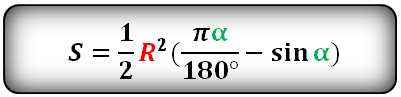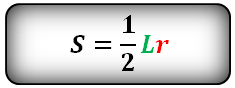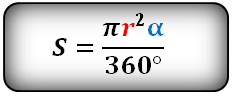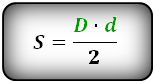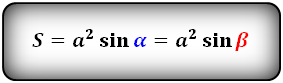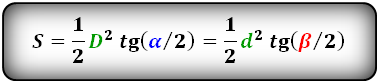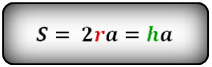Найти площадь треугольника через тангенс

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Площадь равнобедренного треугольника — формулы вычисления

Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.

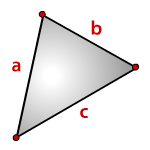
Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.

Каждая из идентичных линий называется боковой, а третья – основанием.

Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).

Площадь (S) фигуры с тремя углами возможно установить:

по двум сторонам и высоте;

через угол между двумя сторонами и величину одной из них;

по двум сторонам;

через синус противолежащего основанию угла;

зная синус прилежащего угла и др.

Видео:✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

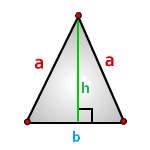
Площадь равнобедренного треугольника через высоту

Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.

У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.

И общая их площадь сводится к:

b — размер основания;

Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.

Вычисления выглядят следующим образом:

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Площадь равнобедренного треугольника через стороны

Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.

Для этого необходима теорема Пифагора, формулы которой видны на картинке,

и формула для отыскания S через биссектрису S = ½ * b * h.

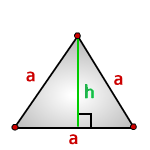
После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.

Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:

При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:

У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:

Видео:Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать

Площадь равнобедренного треугольника через синус угла

В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.

В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:

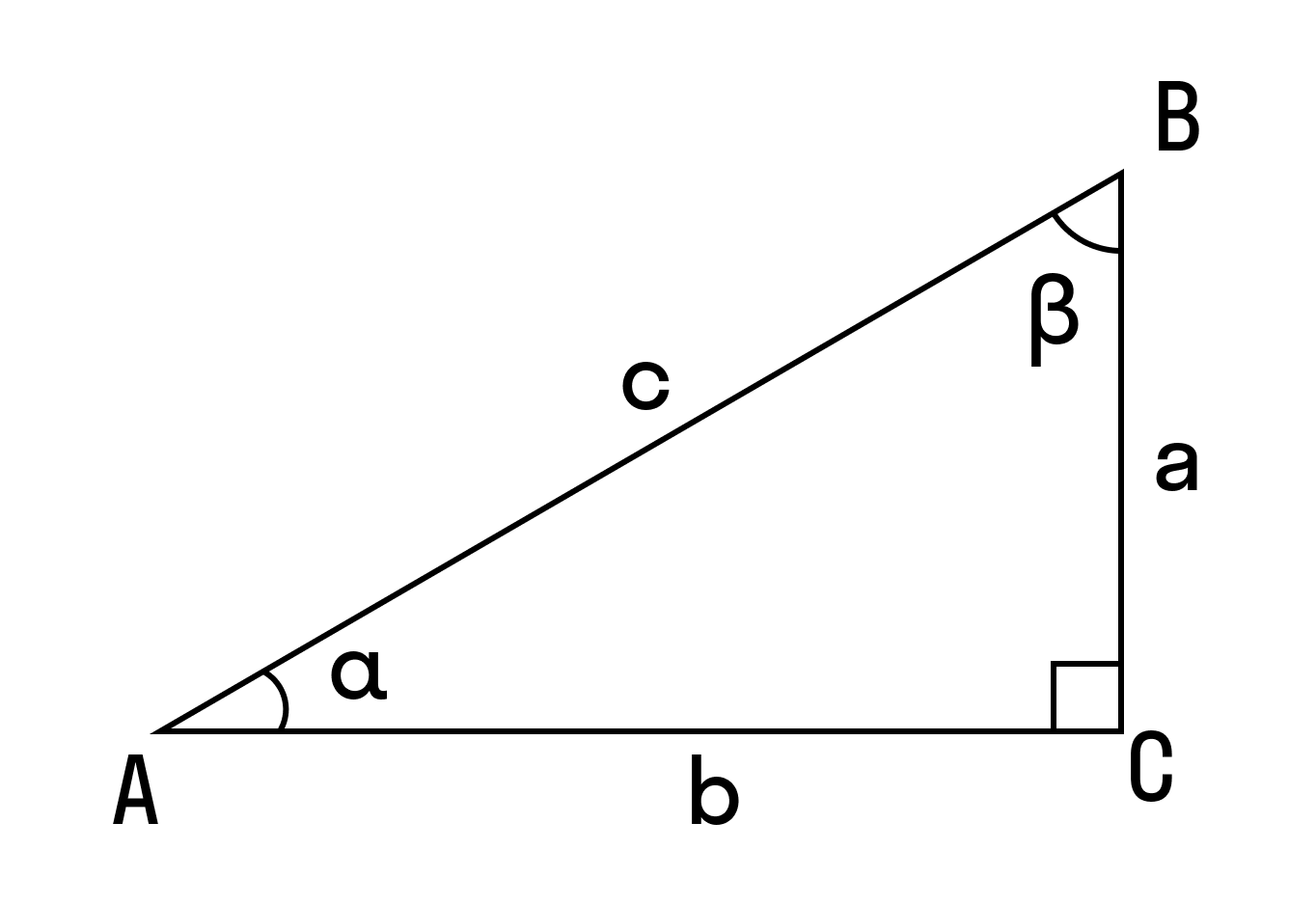
Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Формула площади равнобедренного треугольника через тангенс угла

Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.

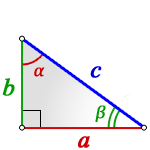
Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:

Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45 0 . Требуется найти площадь треугольника OPQ.

Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.

Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:

180 — 45 — 45 = 90 0 — угол OPQ.

SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2

Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

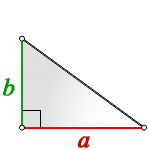
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Видео:100. Теорема о площади треугольникаСкачать

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Видео:Запомни: все формулы для площади треугольникаСкачать

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Видео:Как найти площадь треугольникаСкачать

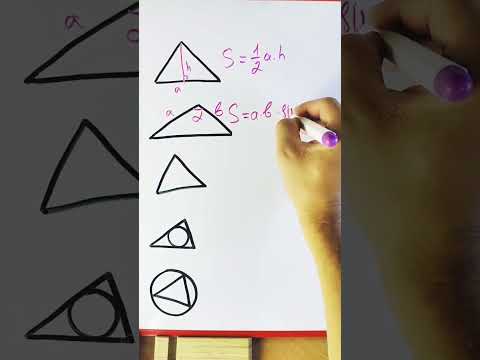
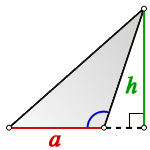
Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

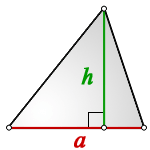
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Видео:ПЛОЩАДЬ ЧЕРЕЗ ТАНГЕНС? / равнобедренный треугольник / #планиметрия #512543Скачать

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Видео:Как найти площадь треугольника без формулы?Скачать

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Площадь прямоугольного треугольника

О чем эта статья:

площадь, 8 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Основные определения

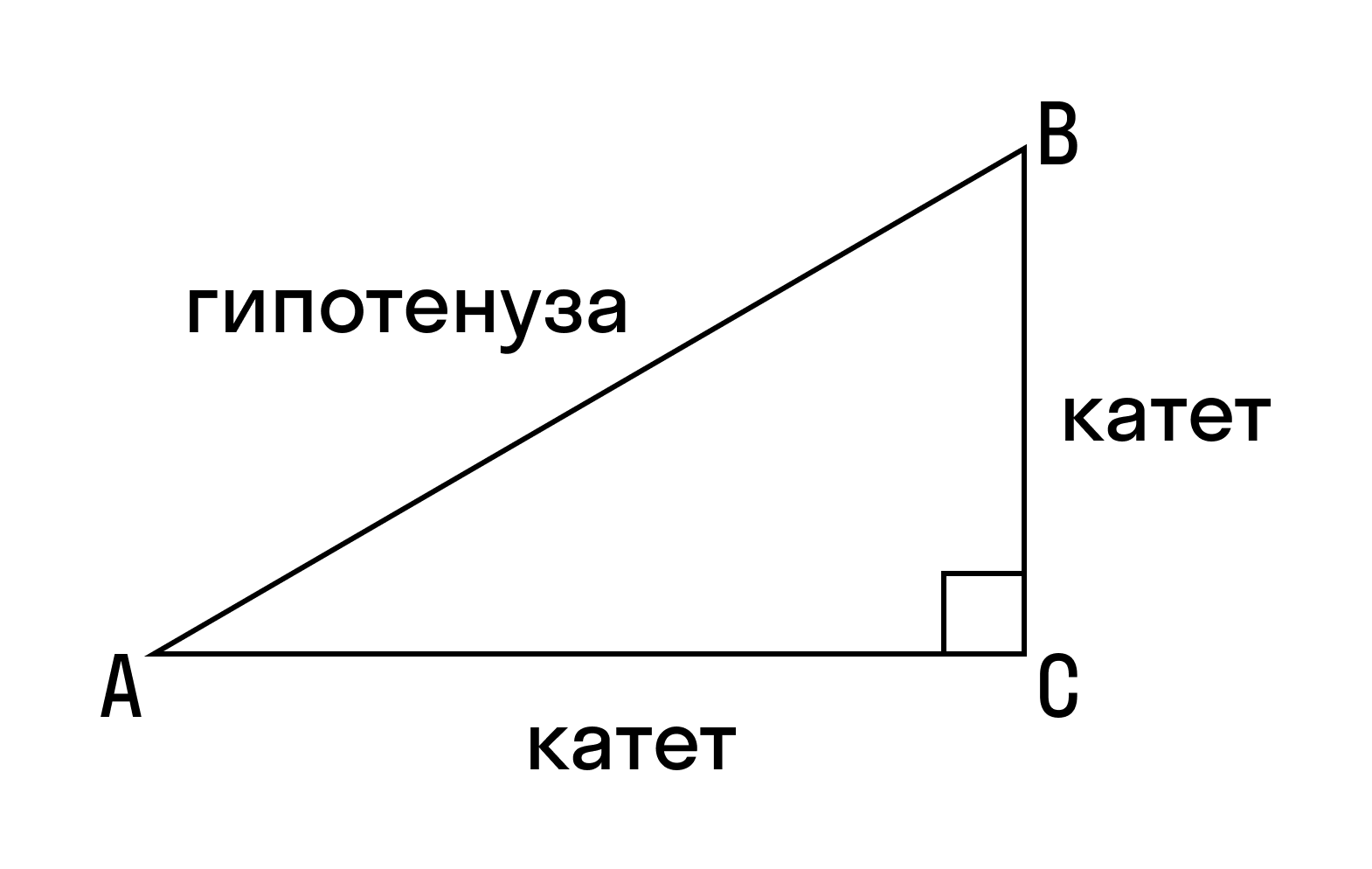
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.

Гипотенуза — это сторона, противолежащая прямому углу.

Катеты — это стороны, прилежащие к прямому углу.

Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.

Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Формула для нахождения площади прямоугольного треугольника через катеты

Чтобы найти площадь, нужно вывести формулу:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.

Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.

Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.

Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.

S = 1/2 (a × b), где a и b — катеты

Видео:Площадь треугольника через синус угла.Решение прямоугольных треугольников.8класс.Скачать

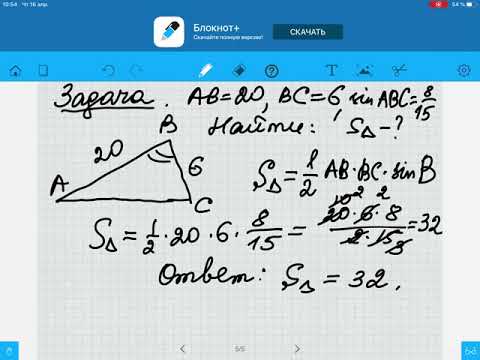
Формула для нахождения площади прямоугольного треугольника через гипотенузу

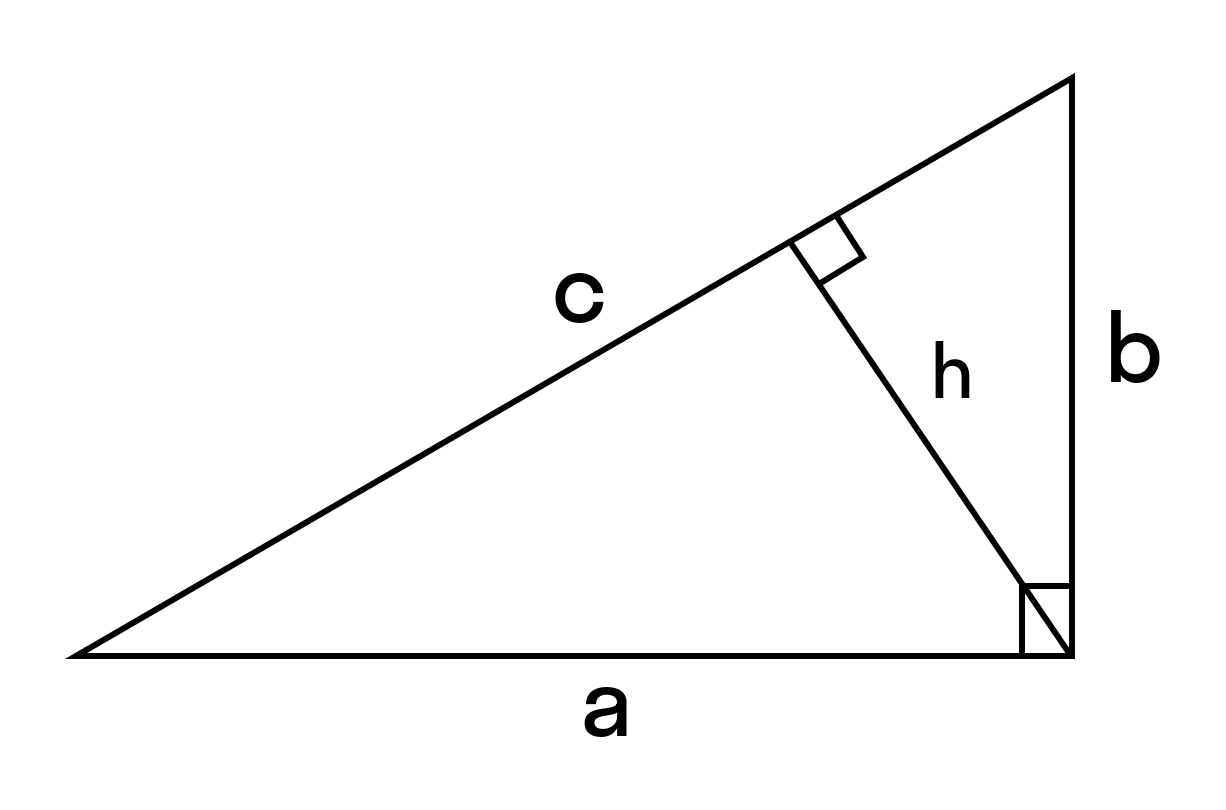
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.

где с — гипотенуза,

Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол

α, β — острые углы

Видео:Как найти катет по углу и другому катету. Как найти площадь треугольника и параллелограмма. 9 классСкачать

Формулы нахождения площади прямоугольного треугольника через катет и угол

α, β — острые углы

Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу

Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:

S прямоугольного треугольника = r (r + c) = c1 × c2

r — радиус вписанной окружности

C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью

Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!

Площадь равнобедренного треугольника — формулы вычисления

Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.

Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.

Каждая из идентичных линий называется боковой, а третья – основанием.

Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).

Площадь (S) фигуры с тремя углами возможно установить:

по двум сторонам и высоте;

через угол между двумя сторонами и величину одной из них;

по двум сторонам;

через синус противолежащего основанию угла;

зная синус прилежащего угла и др.

Площадь равнобедренного треугольника через высоту

Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.

У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.

И общая их площадь сводится к:

b — размер основания;

Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.

Вычисления выглядят следующим образом:

Площадь равнобедренного треугольника через стороны

Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.

Для этого необходима теорема Пифагора, формулы которой видны на картинке,

и формула для отыскания S через биссектрису S = ½ * b * h.

После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.

Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:

При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:

У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:

Площадь равнобедренного треугольника через синус угла

В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.

В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:

Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.

Формула площади равнобедренного треугольника через тангенс угла

Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.

Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:

Дан равнобедренный треугольник OPQ (см. рис. 1). Известны величины: основание OQ = 5 см и угол QOP = 45 0 . Требуется найти площадь треугольника OPQ.

Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.

Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:

180 — 45 — 45 = 90 0 — угол OPQ.

SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2

Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.

Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла

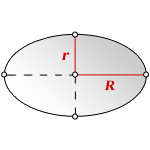
R — большая полуось

r — малая полуось

π ≈ 3.14

Формула площади эллипса, через полуоси:

Калькулятор, вычислить площадь элипса:

1. Формула площади равнобедренной трапеции через стороны и угол

а — нижнее основание

b — верхнее основание

с — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, ( S ):

Формула площади равнобедренной трапеции через стороны и угол, ( S ):

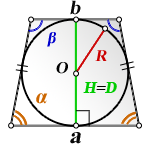
2. Формулы площади равнобедренной трапеции если в нее вписана окружность

R — радиус вписанной окружности

D — диаметр вписанной окружности

O — центр вписанной окружности

H — высота трапеции

α , β — углы трапеции

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, ( S ):

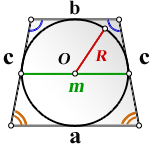
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

R — радиус вписанной окружности

m — средняя линия

O — центр вписанной окружности

c — боковые стороны

а — нижнее основание

b — верхнее основание

Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию ( S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d — диагональ трапеции

α , β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, ( S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

c — боковая сторона

m — средняя линия трапеции

α , β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, ( S ):

5. Формула площади равнобедренной трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, ( S ):

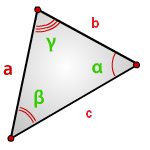
a , b , c — стороны треугольника

α , β , γ — противолежащие углы

Площадь треугольника через сторону и два угла (S):

Формулы для треугольника:

Зная длины всех трех сторон

и используя формулу Герона можно найти площадь разностороннего треугольника

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула ( Герона ) площади треугольника через полупериметр ( S ):

Калькулятор — вычислить, найти площадь треугольника:

Формулы для треугольника:

Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
Высота треугольника это — опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.

Что бы найти площадь треугольника,

для этого надо основание умножить на высоту и разделить на два

1. Площадь разностороннего треугольника

h — высота треугольника

Формула площади треугольника (S):

Калькулятор для расчета площади треугольника

2. Площадь треугольника с тупым углом

h — высота треугольника

Формула площади треугольника с тупым углом (S):

Формулы для треугольника:

Зная у треугольника

две стороны и синус угла между ними, находим по формуле, его площадь

a , b , c — стороны треугольника

α , β , γ — углы

Формулы площади треугольника, через две стороны и угол между ними, (S):

Калькулятор — вычислить, найти площадь треугольника:

Формулы для треугольника:

Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза

1. Если известны только катеты

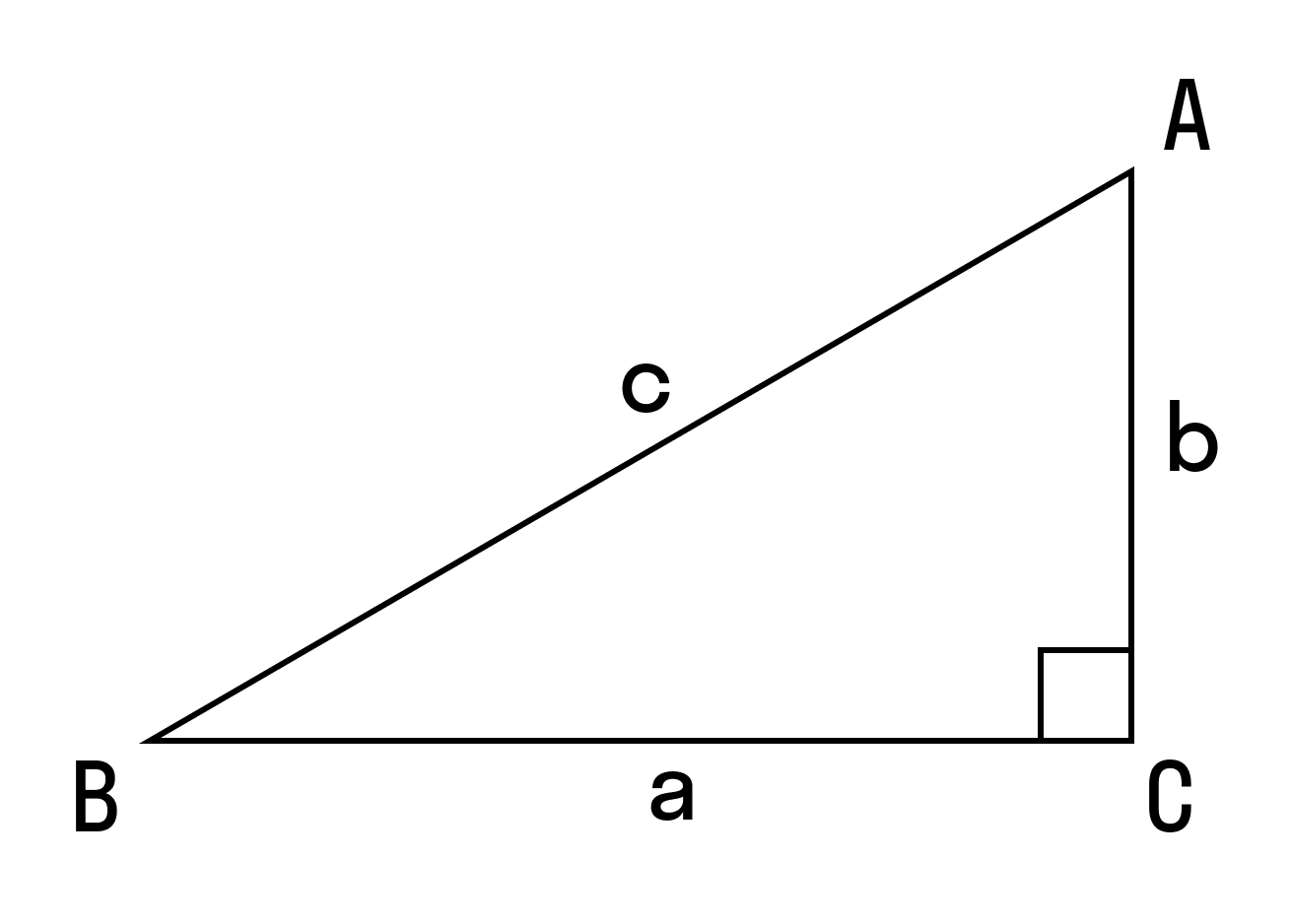
a , b — катеты треугольника

Формула площади треугольника через катеты ( S ) :

2. Если известны острый угол и гипотенуза или катет

c — гипотенуза

a , b — катеты

α , β — острые углы

Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :

Формулы площади прямоугольного треугольника через катет и угол ( S ) :

Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если

то справедливы следующие тождества:

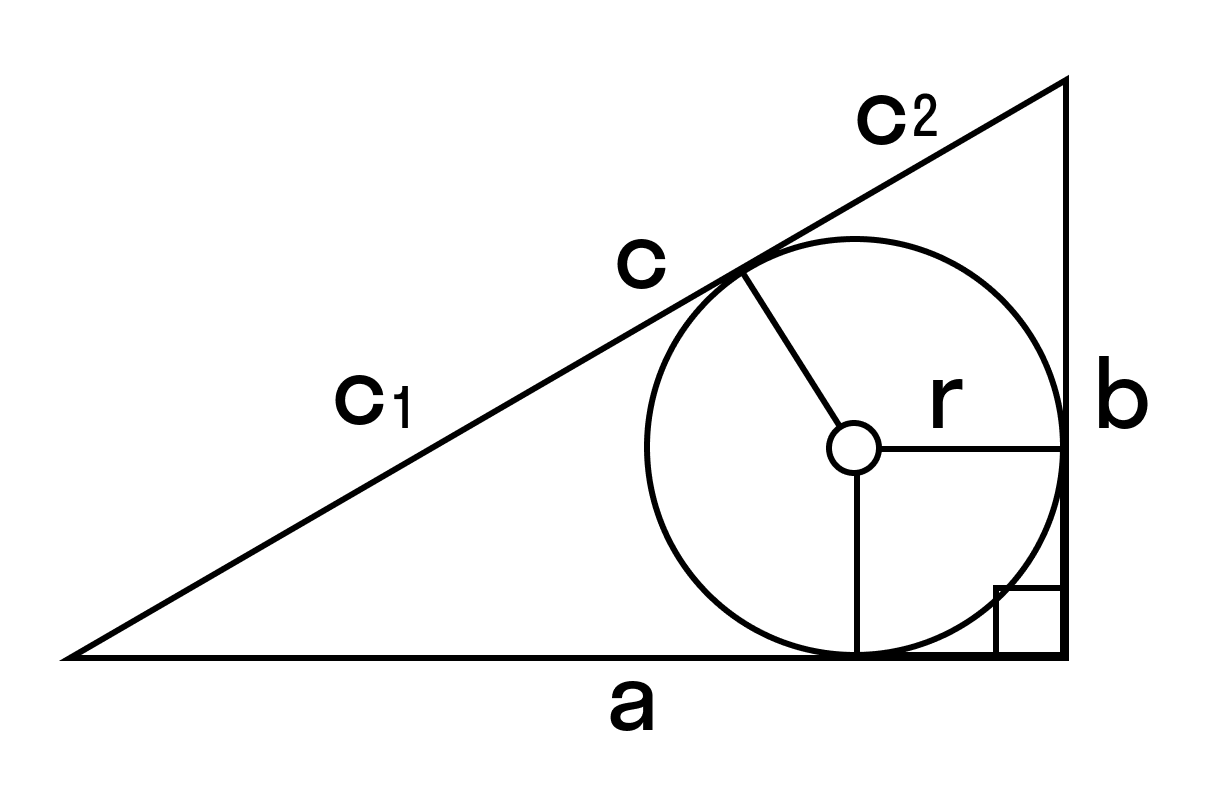
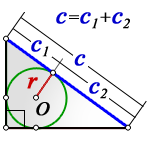
3. Если известны радиус вписанной окружности и гипотенуза

c — гипотенуза

c 1 , c 2 — отрезки полученные делением гипотенузы, точкой касания окружности

r — радиус вписанной окружности

О — центр вписанной окружности

Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :

b — основание треугольника

a — равные стороны

h — высота

Формула площади треугольника через высоту h и основание b , (S):

Калькулятор — вычислить, найти площадь треугольника через высоту и основание:

Формула площади треугольника через, стороны a , b , (S):

Калькулятор — вычислить, найти площадь треугольника через равные стороны и основание:

b — основание треугольника

a — равные стороны

h — высота

Формулы для треугольника:

Если вы знаете сторону или высоту

вы можете найти площадь равностороннего треугольника

a — сторона треугольника

h — высота

Площадь треугольника через сторону a и высоту h , (S):

Площадь треугольника только через сторону a , (S):

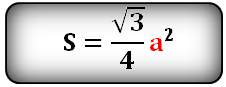
Калькулятор для расчета площади равностороннего треугольника

Площадь треугольника только через высоту h , ( S ):

Калькулятор для расчета площади равностороннего треугольника

a — сторона треугольника

h — высота

Формулы для треугольника:

Формула площади круга, диаметр

Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса

или радиус круга или длину окружности, можно найти его площадь.

r — радиус круга

D — диаметр круга

Формула площади круга, (S):

на тему: Площадь круга

Калькулятор для расчета площади круга через радиус

Калькулятор для расчета площади круга через диаметр

L — длина окружности

О — центр круга

Формула площади круга если известна длина окружности, (S):

на тему: Площадь круга

Калькулятор для расчета площади круга через длину

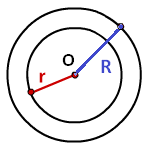
Площадь кольца равна — число π , умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности

R — радиус внешней окружности

r — радиус внутренней окружности

Формула площади кольца (S):

Калькулятор — вычислить, найти площадь кольца

R — радиус внешней окружности

r — радиус внутренней окружности

α — угол сектора AOB, в градусах

Формула площади сектора кольца (S):

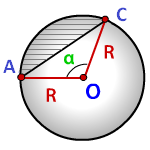
R — радиус круга

α — угол сегмента в градусах

Формула площади сегмента круга (S), отсекаемая хордой AC :

Калькулятор для расчета длины дуги окружности :

Формулы для окружности и круга:

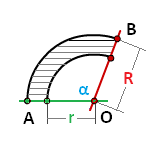
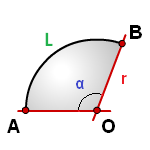
Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол

r — радиус круга

L — длина дуги AB

α — угол сектора круга AOB в градусах

Формула площади сектора круга (S), через длину дуги ( L ):

Формула площади сектора круга (S), через угол ( α ):

Формулы для окружности и круга:

Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

β — тупой угол

Формулы площади ромба через диагонали и углы между сторонами ( S ):

a — сторона ромба

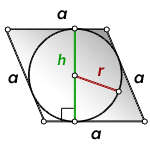
h — высота

r — радиус вписанной окружности

Формула площади ромба через высоту или радиус вписанной окружности ( S ):

1. Формула площади параллелограмма через стороны и углы

a, b — стороны параллелограмма

α , β — углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

Калькулятор — вычислить, найти площадь параллелограмма:

2. Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H _b — высота на сторону b

H _a — высота на сторону a

Формула площади через стороны и высоты параллелограмма, ( S ):

3. Формула площади параллелограмма через диагонали и угол между ними

D — большая диагональ

d —меньшая диагональ

α , β — углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , ( S ):

Калькулятор — вычислить, найти площадь параллелограмма:

Формулы для параллелограмма: