Найти площадь подобного треугольника (2 видео)

Подобные треугольники

Содержание

Определение
Признаки подобия треугольников
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
Отношение площадей подобных треугольников
Определение подобных треугольников
Пропорциональные отрезки
Подобные треугольники
Готовые работы на аналогичную тему
Площади подобных треугольников
Задачи, связанные с понятием подобия треугольника
💡 Видео

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Определение

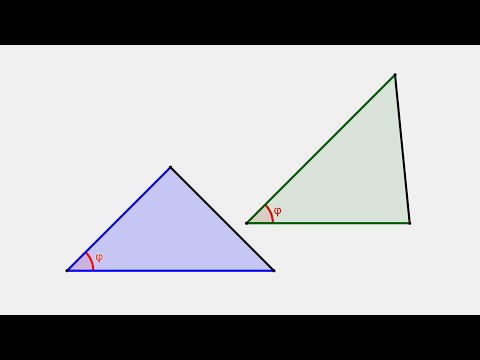
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Свойства подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

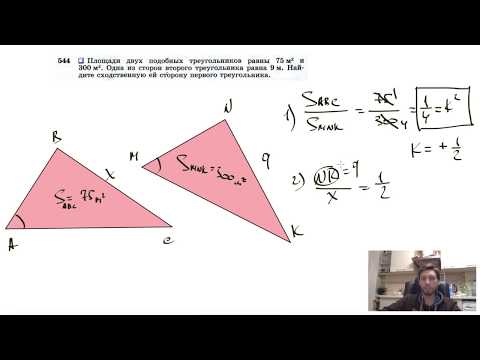
Видео:№544. Площади двух подобных треугольников равны 75 м2 и 300 м2. Одна из сторон второгоСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Отношение площадей подобных треугольников

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы введем понятие подобных треугольников и рассмотрим теорему об отношении их площадей. Затем будет рассмотрен ряд примеров на применение этой теоремы.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение»

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Определение подобных треугольников

Вы будете перенаправлены на Автор24

Видео:Отношение площадей подобных треугольниковСкачать

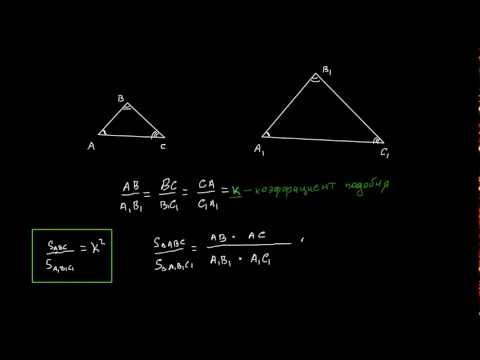
Пропорциональные отрезки

Для введения понятия подобия вначале нам необходимо вспомнить понятие пропорциональных отрезков. Вспомним также определение отношения двух отрезков.

Отношением двух отрезков называется отношение их длин.

Отрезки $AB$ и $CD$ называются пропорциональными отрезкам $A_1B_1$ и $C_1D_1$, то есть

Понятие пропорциональности отрезков имеет место и для большего числа отрезков. Пусть, к примеру, $AB=2$, $CD=4$, $A_1B_1=1$, $C_1D_1=2$, $A_2B_2=4$, $C_2D_2=8$, тогда

То есть отрезки $AB$, $A_1B_1$, $ A_2B_2$ пропорциональны отрезкам $CD$, $C_1D_1$, $C_2D_2$.

Видео:60. Отношение площадей подобных треугольниковСкачать

Подобные треугольники

Вспомним для начала, что вообще представляет себе понятие подобия.

Фигуры называются подобными, если они имеет одинаковую форму, но разные размеры.

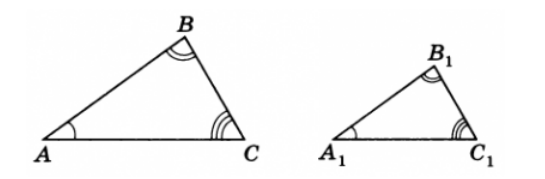
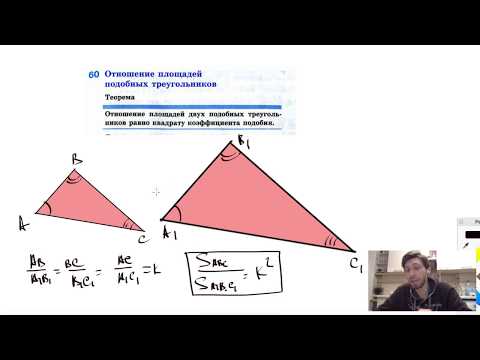
Разберемся теперь с понятием подобных треугольников. Рассмотрим рисунок 1.

Рисунок 1. Два треугольника

Пусть у этих треугольников $angle A=angle A_1, angle B=angle B_1, angle C=angle C_1$. Введем следующее определение:

Стороны двух треугольников называются сходственными, если они лежат напротив равных углов этих треугольников.

Готовые работы на аналогичную тему

На рисунке 1, стороны $AB$ и $A_1B_1$, $BC$ и $B_1C_1$, $AC$ и $A_1C_1$ сходственные. Введем теперь определение подобных треугольников.

Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть

[angle A=angle A_1, angle B=angle B_1, angle C=angle C_1,] [frac=frac<_1>=frac]

На рисунке 1 изображены подобные треугольники.

Обозначение: $ABCsim A_1B_1C_1$

Для понятия подобия существует также понятие коэффициента подобия.

Число $k$, равное отношению сходственных сторон подобных фигур называется коэффициентом подобия этих фигур.

Видео:Отношение площадей подобных треугольников | Геометрия 7-9 класс #58 | Инфоурок Скачать

Площади подобных треугольников

Рассмотрим теперь теорему об отношении площадей подобных треугольников.

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, то есть

Доказательство.

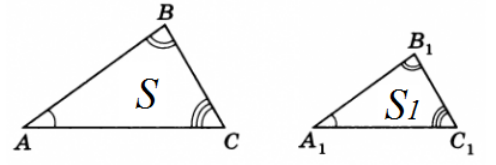
Рассмотрим два подобных треугольника и обозначим их площади, соответственно $S$ и $S_1$ (рис. 2).

Для доказательства этой теоремы вспомним следующую теорему:

Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.

Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то, по определению,$angle A=angle A_1$. Тогда, по теореме 2, получим, что

Видео:8 класс Отношение площадей подобных фигурСкачать

Задачи, связанные с понятием подобия треугольника

Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Стороны первого треугольника $AB=2, BC=5, AC=6$. Коэффициент подобия данных треугольников $k=2$. Найти стороны второго треугольника.

Решение.

Данная задача имеет два возможных решения.

Тогда $A_1B_1=kAB, _1=kBC, A_1C_1=kAC$.

Следовательно, $A_1B_1=4, _1=10, A_1C_1=12$

Следовательно, $A_1B_1=1, _1=2,5, A_1C_1=3$.

Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Сторона первого треугольника $AB=2$, соответствующая сторона второго треугольника $A_1B_1=6$. Высота первого треугольника $CH=4$. Найти площадь второго треугольника.

Решение.

Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то $k=frac=frac$.

Найдем площадь первого треугольника.

[S=fracABcdot CH=fraccdot 2cdot 4=4]

По теореме 1, имеем:

Ответ: $36$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 25 03 2021