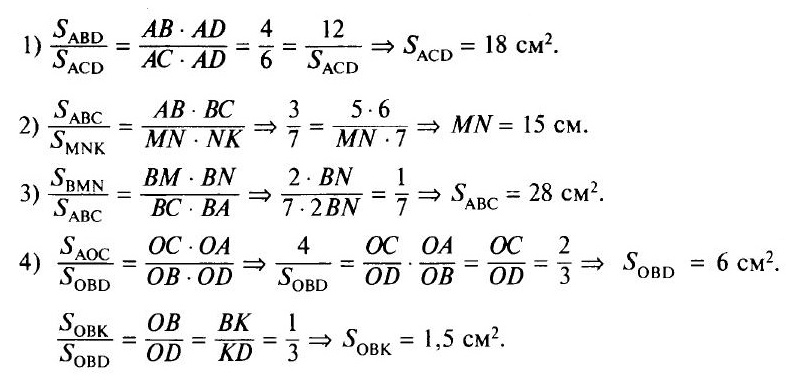Найти отношение площади треугольника

Найти отношение площади треугольника

Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников. Вернуться к Списку уроков Тематического планирования.

Урок 32. Отношение площадей
подобных треугольников

Основные дидактические цели урока: закрепить понятия пропорциональных отрезков и подобных треугольников; совершенствовать навыки решения задач на применение свойства биссектрисы треугольника и определения подобных треугольников; рассмотреть теорему об отношении площадей подобных треугольников и показать ее применение в процессе решения задач.

Ход урока

I. Организационный момент

(Учитель сообщает тему урока, формулирует цели урока.)

II. Актуализация знаний учащихся. Мотивация к учебной деятельности

1. Теоретический опрос.

(Один ученик оформляет доказательство теоремы на доске.)
1) Ответить на вопросы 1—3 учебника.
2) Доказать свойство биссектрисы треугольника.

2. Проверка домашнего задания.

(Учитель проверяет решение задач № 538, 542. Два ученика готовят решение на доске.)

Задача № 538

• В каком отношении биссектриса AD треугольника АВС делит сторону ВСР.
• Что можно сказать об отношении отрезков АВ и АС?
• Составьте уравнение, используя отношение отрезков АВ и АС и значение периметра треугольника АВС.

Задача № 542

• Какие треугольники называются подобными?
• Чему равно отношение сходственных сторон MN и ВС, KN и AC?
• Чему равны стороны треугольника KMN?

3. Работа по индивидуальным карточкам.

(3—6 учеников работают по карточкам.)

I уровень сложности

1. Треугольники KPF и ЕМТ подобны, причем КР : ME = PF : МТ = КЕ : ЕТ, ∠F = 30°, ∠Е = 49°. Найдите остальные углы этих треугольников.
2. Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см. Найдите периметр треугольника АВС, если известно, что АВ = 9 см.

II уровень сложности

1. ΔВВС подобен ΔАВС (рис. 7.3), AD = 16 см, DC = 9 см. ∠ABC и ∠BDA — тупые. Найдите ВС.
2. Периметр треугольника равен 70 см, две его стороны равны 24 см и 32 см. Найдите отрезки, на которые биссектриса треугольника делит его третью сторону.

III уровень сложности

1. Диагональ АС делит трапецию ABCD на два подобных треугольника АВС и ACD, ВС = 8 см, AD = 18 см. Найдите АС.
2. В равнобедренном треугольнике точка Е — середина основания АС, а точка К делит сторону ВС в отношении 2:5, считая от вершины С. Найдите отношение, в котором прямая BE делит отрезок АК.
3. Решение задач по готовым чертежам для подготовки к восприятию нового материала (работа в парах).

Ответы и указания к задачам по готовым чертежам:

(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:

• оценка «5» — правильно решены три-четыре задачи;
• оценка «4» — правильно решены две задачи;
• оценка «3» — правильно решена одна задача;
• оценка «2» — не ставится.

III. Работа по теме урока

(Учитель делит класс на группы для решения задания творческого характера. После завершения работы заслушиваются и обсуждаются варианты решений.)

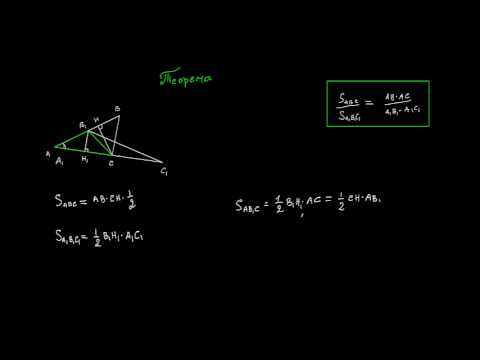
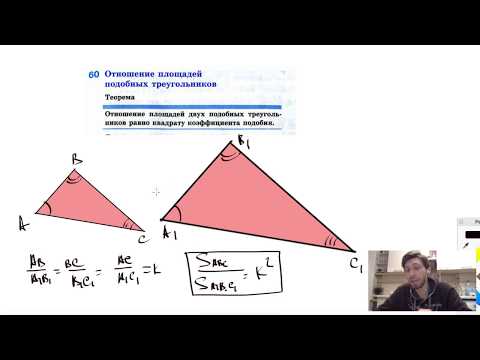
Задание. Треугольники АВС и А1В1С1 подобны с коэффициентом подобия k. Найти отношение их площадей.

Вывод. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

IV. Закрепление изученного материала

1. Работа в рабочих тетрадях. Решить задачу № 54. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)
2. Решить задачу № 545 (работа в парах). (После завершения работы заслушиваются и обсуждаются варианты решений.)

Задача № 545

Вопросы для обсуждения.

• Чему равно отношение площадей подобных треугольников, если их сходственные стороны относятся как 6 : 5?
• Верно ли составлено уравнение исходя из условий задачи?

1. Решить задачи № 547, 548 (работа в группах). (После завершения работы заслушиваются и обсуждаются варианты решений.)

V. Самостоятельная работа

I уровень сложности

II уровень сложности

III уровень сложности

VI. Рефлексия учебной деятельности

1. Какие треугольники называются подобными?
2. Сформулируйте свойство биссектрисы треугольника.
3. Что можно сказать о площадях подобных треугольников?

Домашнее задание

1. П. 60, вопросы 4 (учебник, с. 158).
2. Решить задачи № 543, 544, 546, 549.
3. Решить дополнительные задачи.

I уровень сложности: В подобных треугольниках АВС и KMN равны углы В и М, С и N, АС = 3 см, KN = 6 см, MN = 4 см, ∠AX = 30°. Найдите ВС, ∠K; отношение площадей треугольников AВС и KMN; АЕ и BE, если известно, что СЕ — биссектриса треугольника АВС, АВ = 3,5 см.

II уровень сложности: В прямоугольном треугольнике ABC ∠C = 90°, ∠B = 30°, АВ = 12 см, CD — высота. Докажите, что ΔACD подобен ΔАВС, найдите отношение их площадей и отрезки, на которые биссектриса угла А делит катет ВС.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников.

Найти отношение площади треугольника

В элементарной математике, самыми трудными считаются геометрические задачи. Как научиться решать геометрические задачи, особенно сложные, конкурсные? При решении геометрических задач, как правило, алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не просто. Поэтому, желательно в каждой теме выработать какие-то общие положения, которые полезно знать всякому решающему геометрические задачи.
Предлагаем один из алгоритмов решения многих геометрических задач – метод площадей, т.е. решение задач с использованием свойств площадей.

Основные свойства площадей.

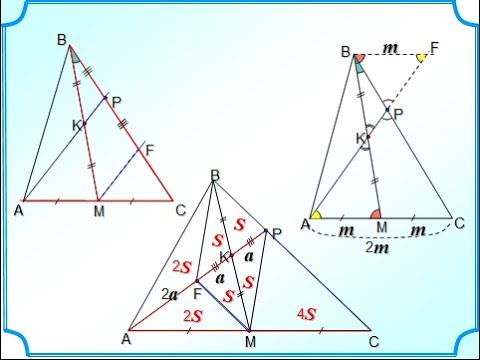
Свойство №1

Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться.Доказательство: Рассмотрим ▲ ABC и ▲ ADC. Они имеют общее основание и равные высоты, так как прямые AC и BD параллельные, то расстояние между ними равно h — высоте ▲ ABC и ▲ ADC . Если площадь треугольника находится по формуле $$S = frac cdot a cdot h$$, то $$S_ = S_ = frac cdot AC cdot h$$.

Свойство №2

Доказательство: Пусть h₁ = h₂ в двух треугольниках с основаниями a и b.
Рассмотрим отношение площадей этих треугольников $$frac<S_><S_>= frac<frac cdot a cdot h_><frac cdot b cdot h_>$$.
Упростив, получим $$frac<S_><S_>= frac$$.

Доказательство: Рассмотрим ▲ABC и ▲MBN с общим углом B , где AB = a, BC = b, MB = a₁и NB = b₁. Пусть S₁ = S_MBN и S₂ = S_ABC . Используя формулу площади треугольника вида $$S = frac cdot a cdot b cdot singamma$$, рассмотрим отношение площадей ▲ABC и ▲MBN .

Свойство №4

Отношение площадей подобных треугольников равны квадрату коэффициента подобия.

Свойство №3 Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.

Доказательство: Рассмотрим ▲ABC и ▲MBN . Пусть AB = k MB, BC = k NB и $$angle ABC = angle MBN$$. Используя формулу площади треугольника вида $$S = frac cdot a cdot b cdot singamma$$ , рассмотрим отношение подобных площадей ▲ABC и ▲MBN . Тогда $$frac<S_><S_> = frac<frac cdot AB cdot BC cdot sin B><frac cdot MB cdot NB cdot sin B>= frac = k^$$ .

Медиана треугольника делит его на две равновеликие части.

Доказательство: Рассмотрим ▲ABC . Пусть медиана BM , тогда $$AM = MC = fracAC$$. Медиана делит треугольник на два с одинаковой высотой. Найдем площади треугольников ▲ABM и ▲MBC по формуле $$S = fraccdot a cdot h$$. Получим $$S_ = fraccdot AM cdot h$$ и $$S_ = fraccdot MC cdot h$$. Значит $$S_ = S_$$.

Свойство №6

Медианы треугольника делят его на три равновеликие части.Доказательство: Рассмотрим ▲ABC . Проведем медианы из всех вершин, которые пересекаются в точке O. Получим треугольники ▲AOB , ▲BOC , ▲AOC . Пусть их площади равны соответственно S₁, S₂, S₃. А площадь ▲ABC равна S. Рассмотрим ▲ABK и ▲CBK , они равной площади, т.к. BK медиана. В треугольнике ▲AOC OK — медиана, значит площади треугольников ▲AOK и ▲COK равны. Отсюда следует, что S₁ = S₂ . Аналогично можно доказать, что S₂ = S₃ и S₃ = S₁ .

Средние линии треугольника площади S отсекают от него треугольники площади .

Доказательство: Рассмотрим ▲ABC . NM — средняя линия в треугольнике и она равна половине основания AC. Если S_ABC = S , то $$S_ = frac cdot NM cdot h_= frac(frac cdot AC)(fraccdot h) = fraccdot S$$. Аналогично можно доказать, что площади всех треугольников равны одной четвертой части площади ▲ABC .

Медианы треугольника делят его на 6 равновеликих частей.

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Отношение площадей подобных треугольников

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы введем понятие подобных треугольников и рассмотрим теорему об отношении их площадей. Затем будет рассмотрен ряд примеров на применение этой теоремы.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение»

🔥 Видео

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Найти отношение площади треугольника к площади квадратаСкачать

Отношение площадей треугольниковСкачать

Отношение площадей треугольников с равным угломСкачать

Задание 24 Отношение площадей 3 способа решенияСкачать

60. Отношение площадей подобных треугольниковСкачать

#57. Отношение площадей треугольников — самые надежные отношения!Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать

Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Сможешь найти площадь треугольника? Задача про отношение площадейСкачать

Математика ОГЭ Задание 26 Отношение площадейСкачать

100. Теорема о площади треугольникаСкачать

Отношение площадей подобных треугольников.Скачать

Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Поделиться или сохранить к себе:

Смотрите также

Площадь равнобедренного треугольника

Площадь прямоугольного треугольника

Плечо силы в треугольнике

Плетение треугольника мозаичным плетением

Плетение треугольника из лозы

Плетение треугольника из веревки

Плетение из газетных трубочек треугольник

Плетение из бисера треугольник