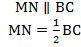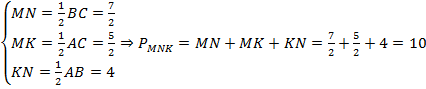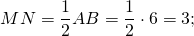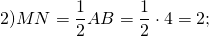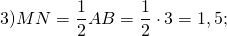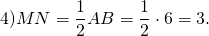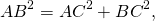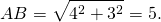Найдите среднюю линию треугольника параллельную (3 видео)

Как найти среднюю линию треугольника?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Содержание

Понятие треугольника
Понятие средней линии треугольника
Понятие средней линии прямоугольного треугольника
Свойства средней линии треугольника
Теорема о средней линии треугольника
Средняя линия треугольника на клетчатой бумаге
Что такое средняя линия треугольника
Определение средней линии треугольника
Свойства средней линии треугольника
Свойство 1
Свойство 2
Свойство 3
Свойство 4
Признак средней линии треугольника
Пример задачи
📸 Видео

Видео:Площадь треугольника ABC равна 36. DE – средняя линия, параллельная стороне AB.Скачать

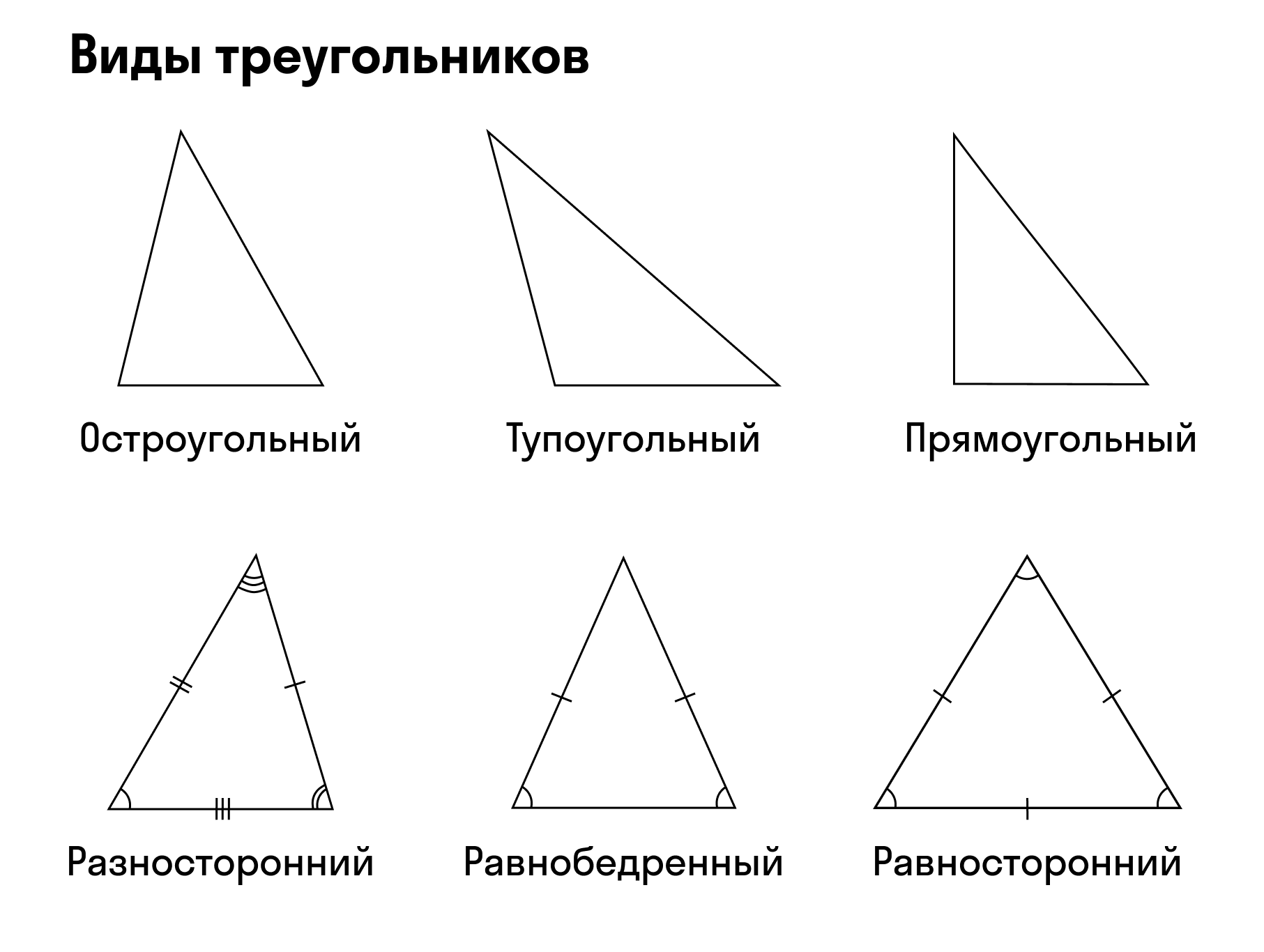
Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

В треугольнике против большего угла лежит большая сторона — и наоборот.
Сумма углов треугольника равна 180 градусов.
Все углы равностороннего треугольника равны 60 градусам.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Найди длину средней линии | Подготовка к ОГЭСкачать

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

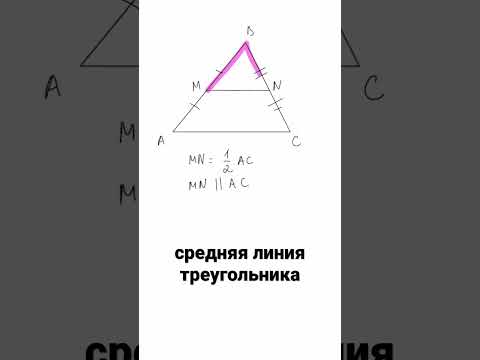
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

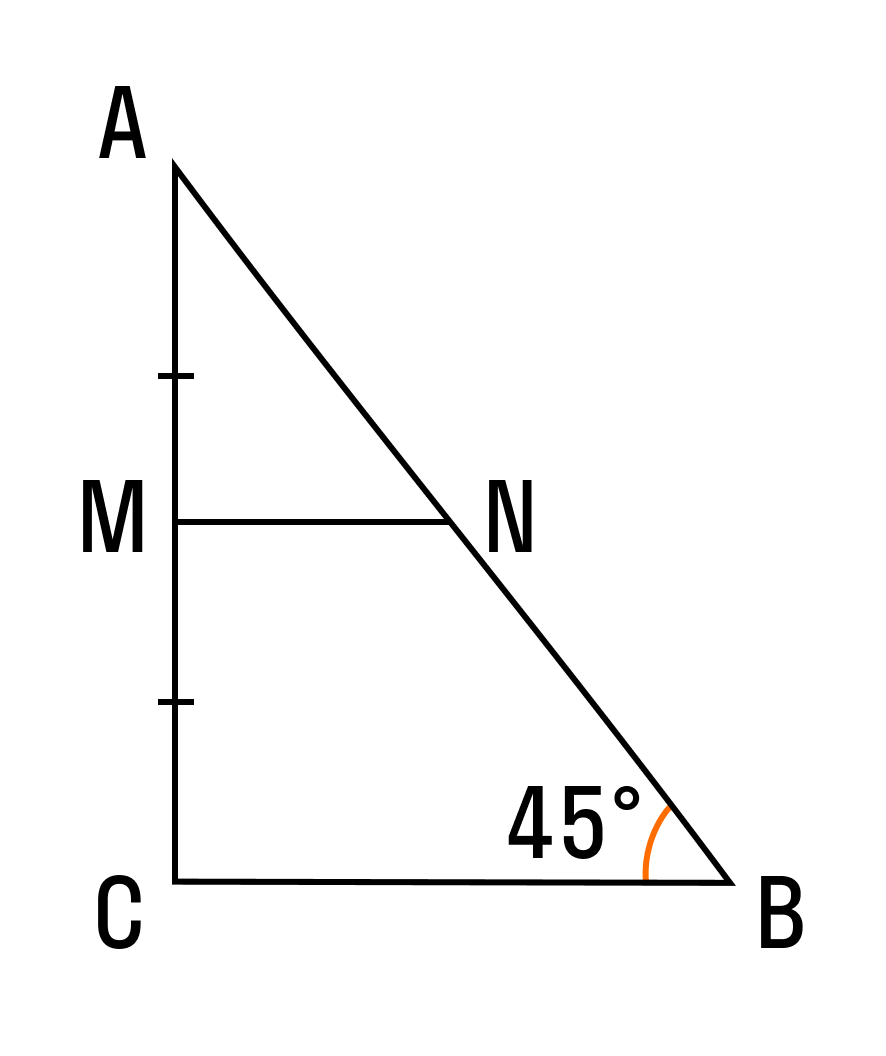
Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Видео:В треугольнике ABC DE – средняя линия ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

Средняя линия равна половине длины основания и параллельна ему.
Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Видео:Площадь треугольника ABC равна 24, DE - средняя линия, параллельная стороне AB. Найдите площадь треуСкачать

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

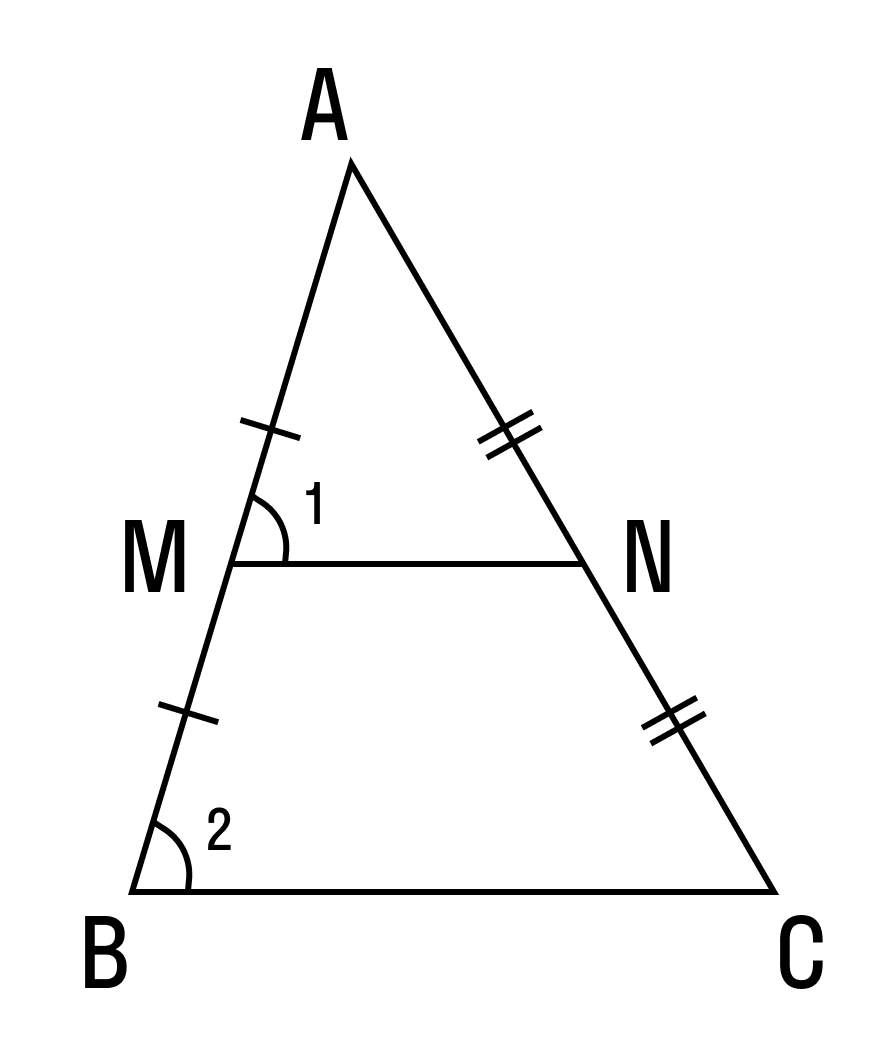
Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.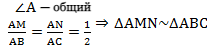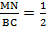

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

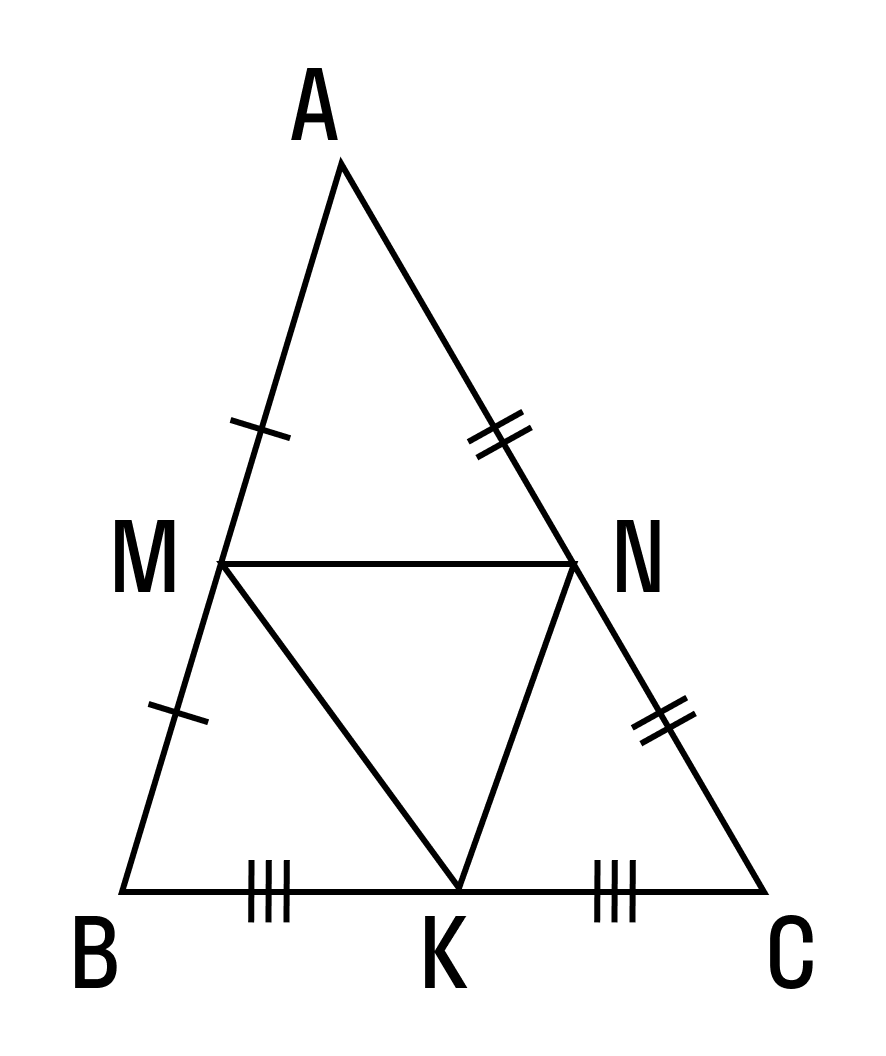
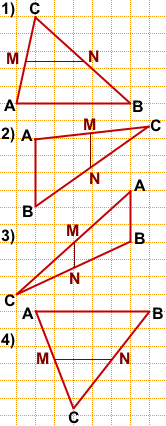
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Видео:ЗАДАНИЕ 1|ЕГЭ ПРОФИЛЬ| Площадь треугольника ABC равна 52, DE-средняя линия, параллельная стороне AB.Скачать

Средняя линия треугольника на клетчатой бумаге

Рассмотрим, как может быть найдена средняя линия треугольника по рисунку на клетчатой бумаге.

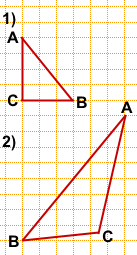
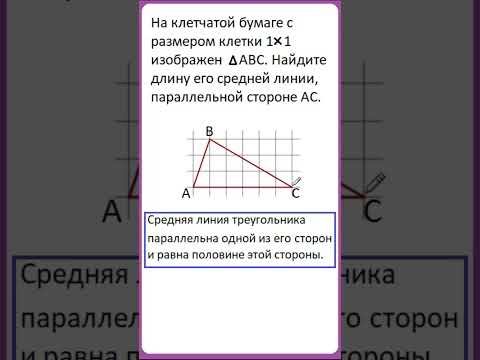
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.

Найдите длину его средней линии, параллельной стороне AB.

Как правило, в таких заданиях на чертеже треугольник расположен таким образом, что по клеточкам посчитать длину средней линии невозможно.

Но задача легко разрешима с применением свойства средней линии треугольника:

средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.

Следовательно, чтобы найти длину средней линии, параллельной стороне AB, надо найти длину отрезка AB.

Длина искомой средней линии равна её половине.

А как быть, если длину стороны треугольника посчитать по клеточкам не получается?

Возможно, в этом случае сторону треугольника можно найти с помощью теоремы Пифагора.

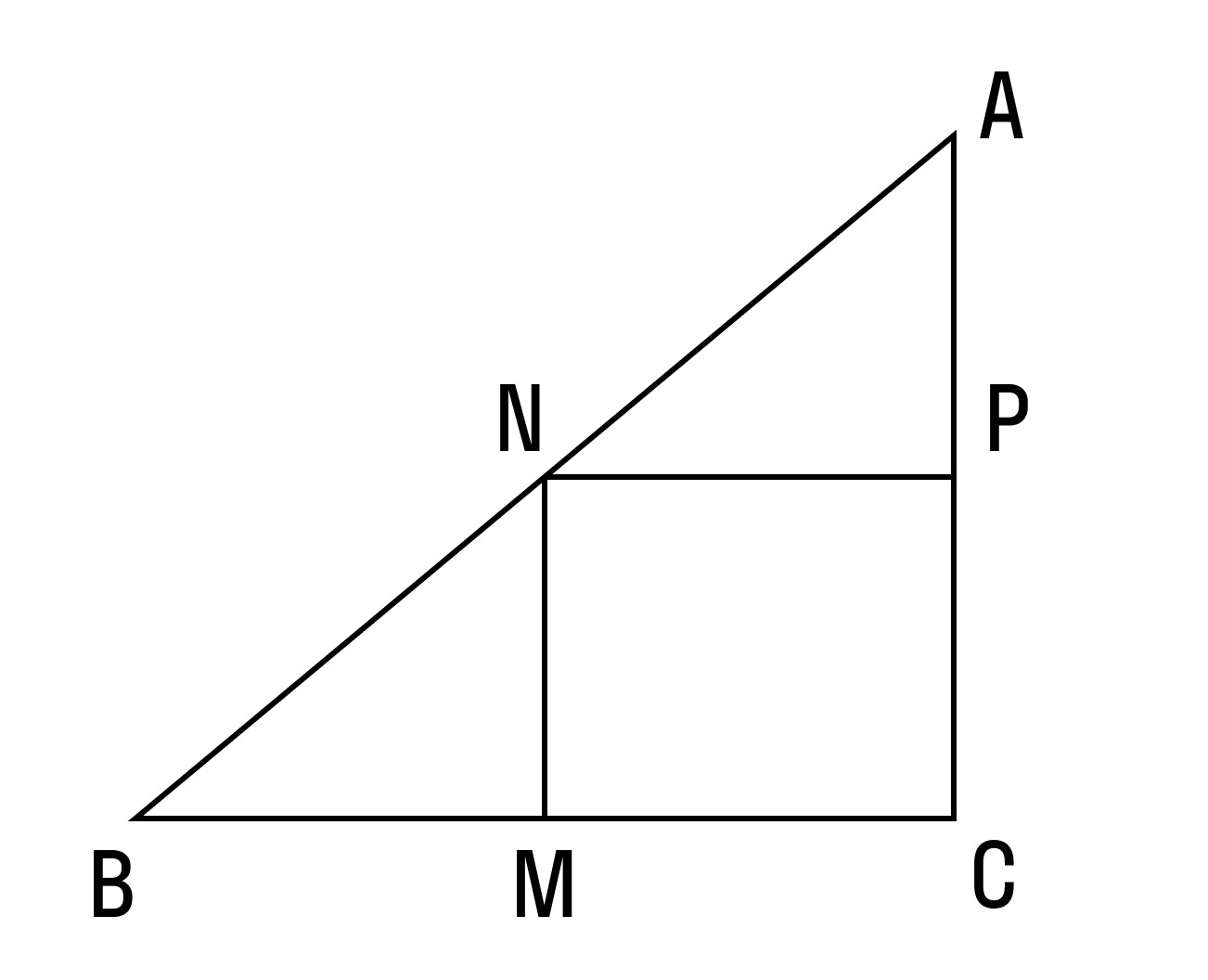
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.

Найдите длину его средней линии, параллельной стороне AB.

1)В прямоугольном треугольнике ABC AB — гипотенуза.

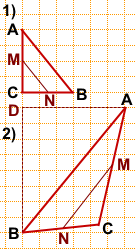
По теореме Пифагора

Средняя линия MN равна половине гипотенузы:

2)Достроим по клеточкам прямоугольный треугольник ABD с гипотенузой AB.

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Что такое средняя линия треугольника

В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Определение средней линии треугольника

Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

KL – средняя линия треугольника ABC
K – середина стороны AB: AK = KB
L – середина стороны BC: BL = LC

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

На рисунке выше:

Свойство 2

Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

На рисунке выше:

△KBL ∼ △ABC (подобие по пропорциональности всех сторон)
Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL.
S_△ABC = 4 ⋅ S_△KBL

Свойство 3

В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.

Свойство 4

Три средние линии треугольника делят его на 4 равных по площади треугольника.

Видео:Теорема о средней линии треугольникаСкачать

Признак средней линии треугольника

Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

Видео:18 ЗАДАНИЕ ОГЭ ПРО СРЕДНЮЮ ЛИНИЮ ТРЕУГОЛЬНИКАСкачать

Пример задачи

Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.