В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
- Формулы вычисления радиуса описанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равносторонний треугольник
- Примеры задач
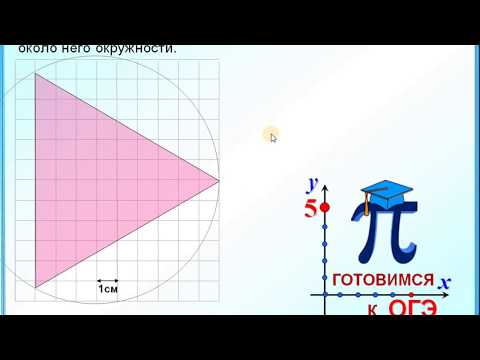
- Треугольник ABC — правильный, его сторона равна 18 см. Найдите радиус ОВ описанной около него окружности.
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Прямоугольник и прямоугольный треугольник: радиус вписанной и описанной окружности. Задание В6
- 📺 Видео
Видео:Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Видео:Геометрия Радиус окружности описанной около треугольника ABC равен 6 см Найдите радиус окружностиСкачать

Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
Видео:2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

Треугольник ABC — правильный, его сторона равна 18 см. Найдите радиус ОВ описанной около него окружности.
Видео:Задание 16 ОГЭ по математике. Окружность описана около равностороннего треугольника. Задача 2Скачать

Ваш ответ
Видео:Радиус окружности описанной около равностороннего треугольникаСкачать
решение вопроса
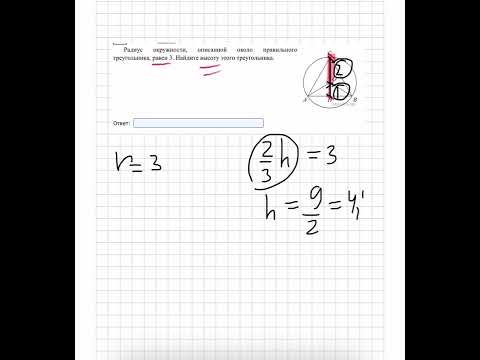
Видео:Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,997
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Прямоугольник и прямоугольный треугольник: радиус вписанной и описанной окружности. Задание В6
При решении задач на нахождение радиуса вписанной или описанной окружности нужно вспомнить такие факты:
1. Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы. Соответственно, радиус окружности, описанной около прямоугольного треугольника равен половине гипотенузы.
2. Центр окружности, описанной около прямоугольника или квадрата, лежит в точке пересечения диагоналей.
3. Радиус окружности, вписанной в квадрат, равен половине стороны квадрата.
4. Центр окружности, вписанной в равносторонний треугольник, а также центр окружности, описанной около равностороннего треугольника лежит в точке пересечения медиан ( высот и биссектрис).
И, так как точка пересечения медиан любого треугольника делит их в отношении 2:1, считая от вершины,
- радиус окружности, вписанной в равносторонний треугольник равен
медианы (высоты, биссектрисы) равностороннего треугольника, и
- радиус окружности, описанной около равностороннего треугольника равен
медианы (высоты, биссектрисы) равностороннего треугольника
5. Радиус окружности, вписанной в прямоугольный треугольник, удобно находить, дважды выразив площадь прямоугольного треугольника:





Рассмотрим примеры решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике:
1 . Задание B7 (№ 27947)
Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.
Центр окружности, описанной около прямоугольника лежит в точке пересечения диагоналей:

2 . Задание B7 (№ 27948)
Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными
ОК- радиус окружности, вписанной в квадрат ABCD:


3 . Задание B7 (№ 27949)
Найдите радиус R окружности, описанной около треугольника ABC, если стороны квадратных клеток равны 1. В ответе укажите 


В ответе требуется указать
4 . Задание B7 (№ 27950)
Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1.

Высота (она же медиана) ВК=3, следовательно,
5 . Задание B7 (№ 27951)
Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.

И.В. Фельдман, репетитор по математике.
📺 Видео
Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Задание 24 ОГЭ по математике #7Скачать

Радиус описанной окружностиСкачать

ОГЭ 2020 задание 17Скачать

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

2053 радиус окружности описанной около правильного треугольника равен 56Скачать









 медианы (высоты, биссектрисы) равностороннего треугольника, и
медианы (высоты, биссектрисы) равностороннего треугольника, и медианы (высоты, биссектрисы) равностороннего треугольника
медианы (высоты, биссектрисы) равностороннего треугольника











