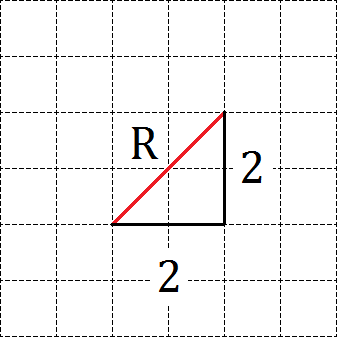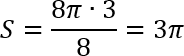In demo mode you can only solve 10 tasks a day.
Please, buy full access.
Please, register:
The answer is wrong. Please, try one more time
Найдите площадь круга, если нанесена сетка с единичными квадратами.
(displaystyle S=) (displaystyle cdot pi )
Из рисунка видно, что радиус круга равен (displaystyle 5) единицам:
Площадь круга для радиуса (displaystyle r) равна (displaystyle pi r^2) Следовательно, площадь круга радиуса (displaystyle r=5) равна
(displaystyle picdot 5^2 =25pi)
Задача B5: площадь сектора
Сегодня мы научимся считать площади кругов и секторов именно в том виде, в котором они встречаются на настоящем ЕГЭ по математике. Основная проблема таких задач B5 — мы не знаем радиус. Большинство учеников просто теряются, когда обнаруживают, что окружность не проходит через узлы сетки, расположенные на горизонтальных и вертикальных диаметрах.
Однако решение есть: достаточно выбрать любую точку окружности, лежащую в узлах координатной сетки (такая точка обязательно найдется, иначе задача составлена некорректно), а затем с помощью теоремы Пифагора найти квадрат радиуса этой окружности.
Все расчеты мы будем выполнять на примере следующей задачи:
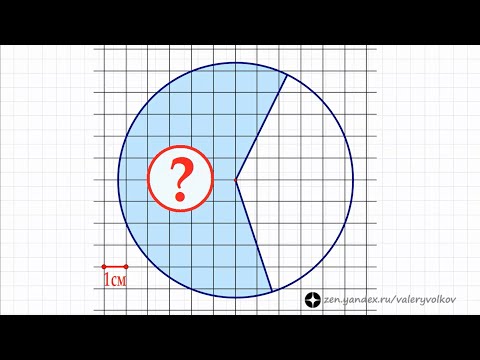
Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S /π.
В первую очередь нам потребуется формула площади круга:
где R — радиус нашего круга. Эту формулу надо знать наизусть. Без нее задачи B5 на площадь круга не решаются вообще.
Но есть и другая проблема. Давайте внимательно посмотрим на рисунок. Для вычисления площади круга (а затем — и сектора) нам надо знать радиус.
Ну и где же здесь радиус? Если мы проведем горизонтальную ось, то получим непонятное число на отрезке [2; 3]. Конечно, можно сказать, что это число ближе к x = 3, но чему именно равно это число, нам неизвестно. А следовательно, использовать эту примерную оценку для решения задачи мы не можем. Надо действовать как-то иначе.
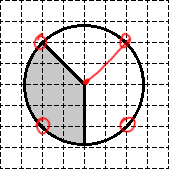
Например, давайте пройдемся по нашей окружности и отметим на ней те точки, которые лежат в узлах координатной сетки. Таких точек будет 4 штуки:
Что дают нам эти точки? А дело в том, что мы можем точно указать, на сколько клеток эти точки отстоят от центра окружности. Например, рассмотрим точку A и центр окружности O :
Мы видим, что точка A отстоит от точки O на 2 клетки по горизонтали и на 2 клетки по вертикали. Получаем прямоугольный треугольник с катетами 2 и 2. Кроме того, гипотенуза нашего прямоугольного треугольника как раз и является радиусом круга, площадь сектора в котором нам и требуется найти.
По теореме Пифагора получаем:
R 2 = 2 2 + 2 2 = 4 + 4 = 8
Теперь мы знаем квадрат радиуса круга: R 2 = 8. Следовательно, зная радиус, мы можем найти площадь всего круга. Достаточно просто подставить найденный радиус в формулу площади. Получим:
S = π R 2 = π · 8 = 8π
Следующий шаг — мы должны понять, какую часть площади круга занимает закрашенный сектор. Для этого давайте схематично разделим исходный круг на 8 равных частей, как пиццу. На полученной разметке закрасим те кусочки, которые входят в состав искомого сектора. Получится вот такая картинка:
Получается, что закрашенных кусочков k = 3. При этом всего кусков было n = 8. Поскольку площади всех секторов, возникающих при «разрезании» исходного круга, одинаковы, можно найти площадь каждого из них, разделив общую площадь на 8. Затем надо умножить полученное число на 3, поскольку в искомом секторе содержится 3 таких одинаковых кусочка. Подставляем все в формулу:
Но это еще не все! В задаче B5 нас просят указать величину S /π. Подставляем и получаем:
Вот мы и нашли ответ. Площадь сектора, деленная на π, равна 3. Как видите, ничего сложного в этой задаче нет. Все, что от нас требуется — правильно выбирать точки на окружности (надо, чтобы они лежали в узлах координатной стеки), а затем подставлять полученные числа в теорему Пифагора.
Надеюсь, этот урок поможет тем ученикам, которым предстоит сдавать ЕГЭ по математике. Задачи на площадь секторов встречаются довольно редко, но к ним надо быть готовым, чтобы они не застали вас врасплох.
Нахождение площади сектора круга
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.
Определение сектора круга
Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.
- AB – дуга сектора;
- R (или r) – радиус круга;
- α – это угол сектора, т.е. угол между двумя радиусами. Также его иногда называют центральным углом.
Формулы нахождения площади сектора круга
Через длину дуги и радиус круга
Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).
Через угол сектора (в градусах) и радиус круга
Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах ( α°) и деленной на 360°.
Через угол сектора (в радианах) и радиус круга
Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (aрад) и квадрата радиуса круга.
Примеры задач
Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.
Решение
Воспользуемся первой формулой, подставив в нее заданные значения:
Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см 2 , а радиус круга – 8 см.
Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше: