Найдите х треугольника mpr

Геометрия | 5 — 9 классы

ДАЮ МНОГО БАЛЛОВ!

Дано : треугольник MPR — равносторонний высота RT = 8 Найти сторону PR.

Лови )) треугольникMPR — равносторонний, МР = MR = PR = 2 * высота * корень3 / 3 = 2 * 8 * корень3 / 3 = 16 * корень3 / 3.

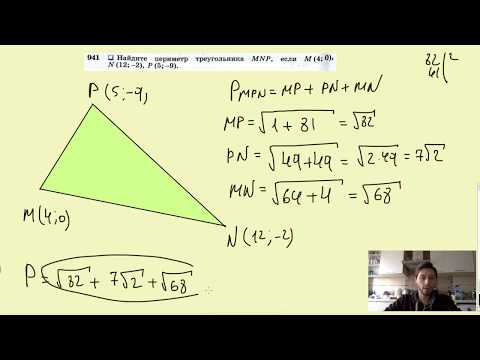
Видео:№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать

Помогите решить СРОЧНО Высота равностороннего треугольника на 4 см меньше его стороны?

Помогите решить СРОЧНО Высота равностороннего треугольника на 4 см меньше его стороны.

Видео:Найдите сторону треугольника на рисункеСкачать

Даны стороны треугольника а, в, с?

Даны стороны треугольника а, в, с.

Найдите высоту треугольника, опущенную на сторону с

Пожалуйста, объясните как найти.

Видео:Найдите третью сторону треугольникаСкачать

ПОМОГИТЕ ПОЖАЛУЙСТА?

ДАЮ МНОГО БАЛЛОВ!

Дано : треугольник MPR — равносторонний высота RT = 8 Найти сторону PR.

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

ДАЮ 40 БАЛОВ Сторона равностороннего треугольника равна 12√3 ?

ДАЮ 40 БАЛОВ Сторона равностороннего треугольника равна 12√3 .

Видео:Математика головоломка геометрия Найти угол х ?Скачать

Высота равностороннего треугольника равна 12√3?

Высота равностороннего треугольника равна 12√3.

Найти его сторону.

Видео:15 задание треугольники огэ по математике / маттаймСкачать

Найдите высоту равностороннего треугольника со стороной а?

Найдите высоту равностороннего треугольника со стороной а.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Найдите высоту равностороннего треугольника со стороной а?

Найдите высоту равностороннего треугольника со стороной а.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Высота равносторонего треугольника равна 13√3?

Высота равносторонего треугольника равна 13√3.

Найдите сторону этого треугольника пожалуйста.

Видео:№1048. Найдите косинусы углов треугольника с вершинами А (2; 8),Скачать

Помогите Найти и решить 5, 6 треугольника через дано, найти, решение даю много баллов?

Помогите Найти и решить 5, 6 треугольника через дано, найти, решение даю много баллов.

Видео:Супер ЖЕСТЬ ➜ Найдите сторону треугольника ➜ Решить без тригонометрииСкачать

У равностороннего треугольника высота проведенная к стороне равна 8см ?

У равностороннего треугольника высота проведенная к стороне равна 8см .

Найти сторону этого треугольника.

Перед вами страница с вопросом ПОМОГИТЕ ПОЖАЛУЙСТА?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Вот, надеюсь поймешь, камера ужасная.

56 — 24 = 32 32 / 2 = 16 24 / 2 = 12 Ответ : 12, 12, 16, 16.

Периметр параллелограммаравен удвоенной сумме 2 — х его сторон или : Р = 2а + 2в. По условию мы знаем 2а = 24смПериметр Р = 56см. Подставим эти значения в формулу : 24 + 2в = 562в = 56 — 242в = 32в = 32 : 2в = 16 см — 1из других сторон. 2а = 24а =..

1. DO = BD / 2 = 9 2. AC = 2 * BO = 22 3. ∠ACD = (180° — 84°) / 2 = 48°.

Соs120° = — 0, 5. Скалярное произведение равно 3·4·(0, 5) = — 6.

Противоположные стороны прямоугольника равны. Периметр прямоугольника находят по формуле Р = 2(а + b), где a и b — стороны прямоугольника, Р — его периметр. Пусть меньшая сторона прямоугольника х см, тогда большая сторона прямоугольника равна (2х) ..

Ответ 28, 28 Сторону берем за Х. И по теореме пифагора находим эту сторону. Так как у на сквадрат то получаем Х ^ 2 + X ^ 2 = 10 ^ 2. 2X ^ 2 = 100. X ^ 2 = 50. Х = корню из 50. Х = 5 корней из 2. Ну а дальше все просто.

Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:№1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:Короткие загадки, которые осилит не каждый профессорСкачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:Найдите биссектрису прямоугольного треугольника с катетами 3 и 5 ★ Как решать?Скачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Найдите х треугольника mpr

9) Рисунок 1: тр. KML — равнобедренный ( КМ = МL )
▪ Отложим отрезок МN, равный отрезку KM, на её продолжении ***** угол NML = 180° — 120° = 60° ***** тр. NML — равносторонний, то есть на стороне ML построили равносторонний треугольник внешним образом ***** KM = ML = MN = NL = x
▪ По теореме Пифагора в тр. KNL:
KN^2 = KL^2 + NL^2

10) тр. RTS — прямоугольный , угол Т = 90°
▪ По теореме Пифагора в тр. RTS:
RS^2 = RT^2 + TS^2
TS^2 = 13^2 — 12^2
TS^2 = 169 — 144 = 25
TS = 5
▪ Площадь треугольника RTS:
S rts = TM • RS / 2 = RT • TS / 2
TM • RS = RT • TS
TM = RT • TS / RS = 12 • 5 / 13 = 60 / 13 = 4_8/13

11) ▪тр. АСВ — равнобедренный ( АС = СВ )
CD — высота, медиана, биссектриса **** AD = DB = 10/2 = 5
▪ По теореме Пифагора в тр. BCD:
CD^2 = 13^2 — 5^2 = 169 — 25 = 144
CD = 12
▪Плошадь тр. АСВ:
S acb = CD • AB / 2 = AE • CB / 2
CD • AB = AE • CB
AE = CD • AB / CB = 12 • 10 / 13 = 120 / 13 =
9_3/13

12) KMRN — ромб ( KM = MR = RN = KN )
▪Диагонали ромба взаимно перпендикулярны, делящие ромб на 4 равных прямоугольных треугольника. Диагонали ромба точкой пересечения делятся пополам ***** Пусть точка О — точка пересечения диагоналей ромба ***** KO = OR = 10/2 = 5 ***** MO = ON = 12/2 = 6
▪ По теореме Пифагора в тр. МОК:
МК^2 = 5^2 + 6^2 = 25 + 36 = 61
МК = V61

13) АBCD — ромб ( AB = BC = CD = AD )
▪Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам ***** Пусть точка О — точка пересечения диагоналей ромба ***** ВO = OD = 12/2 = 6
▪По теореме Пифагора в тр. ВОС:
ОС^2 = 10^2 — 6^2 = 100 — 36 = 64
ОС = 8
АС = 2•ОС = 2•8 = 16

14)
▪Применим для тр. MNK теорему Пифагора:
MK^2 = MN^2 + NK^2
25^2 = 7^2 + 24^2
625 = 49 + 576
625 = 625
Следовательно, по теореме, обратной теореме Пифагора, следует, что тр. МNK — прямоугольный ( угол N = 90° )
▪ Площадь тр. MNK:
S mnk = NL • MK / 2 = MN • NK / 2
NL • MK = MN • NK
NL = MN • NK / MK = 7 • 24 / 25 = 168/25 = 6,72

15) SRLK — прямоугольник
▪Очевидно, что в этой задаче не хватает данных для её решения
Допустим, что в условии задачи известна сторона KS = 5, тогда
▪ По теореме Пифагора в тр. LKS:
SL^2 = KS^2 + KL^2
SL^2 = 5^2 + 12^2 = 25 + 144 = 169
SL = 13

16)
▪ Применим для тр. МКТ теорему Пифагора:
МТ^2 = КТ^2 + МК^2
34^2 = 30^2 + 16^2
1156 = 900 + 256
1156 = 1156
Значит, по теореме, обратной теореме Пифагора, следует, что тр. МКТ — прямоугольный ( угол К = 90° )
▪Пропорциональные отрезки в прямоугольном треугольнике:
МК^2 = MN • MT
16^2 = MN • 34
256 = MN • 34
MN = 256/34 = 128/17 = 7_9/17

🎬 Видео

ОГЭ по математике. Задание 15Скачать

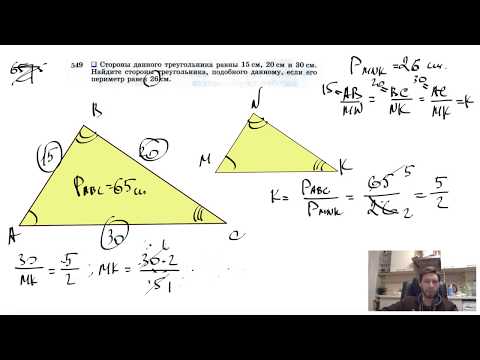
№549. Стороны данного треугольника равны 15 см, 20 см и 30 см. Найдите стороны треугольникаСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Почти никто не решил ➜ Найдите сторону треугольникаСкачать

Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать