Конспект урока
Геометрия, 10 класс
Урок №10. Перпендикуляр и наклонные
Перечень вопросов, рассматриваемых в теме.
- Определение перпендикуляра, наклонной и проекции наклонной на плоскость;
- Доказательство теоремы о трех перпендикулярах;
- Определение угла между прямой и плоскостью.
Глоссарий по теме
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Определение: углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения
Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.
Видео:Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Свойства перпендикуляра и наклонной
Свойства перпендикуляра и наклонной вытекают из теоремы Пифагора и признаков равенства прямоугольных треугольников.
1) Любая наклонная больше перпендикуляра.
Дано: A∉a, AB — перпендикуляр,
Так как AB — перпендикуляр к прямой a, то треугольник ABC — прямоугольный.
По теореме Пифагора AC²=AB²+BC².
Так как BC>0, то и BC²>0.
Следовательно, AB²+BC²>AB². Отсюда, AC²>AB². Поскольку AC>0 и AB>0, то AC>AB.
Что и требовалось доказать.
2) Равные наклонные имеют равные проекции.
Дано: A∉a, AB — перпендикуляр,
AC и AD — наклонные,
BC и BD — их проекции,
Так как AB — перпендикуляр к прямой a, то треугольники ABC и ABD — прямоугольные.
1) AC=AD (по условию);
2) AB — общая сторона.
Следовательно, треугольники ABC и ABD равны (по катету и гипотенузе).
Из равенства треугольников следует равенство соответствующих сторон. Значит, BC=BD.
Что и требовалось доказать.
И обратно: если проекции наклонных равны, то и наклонные тоже равны.
Кроме того, из этого доказательства следует, что равные наклонные образуют равные углы с прямой a; углы между равными наклонными и перпендикуляром также равны.
3) Из двух наклонных больше та, у которой проекция больше.
Дано: A∉a, AB — перпендикуляр,
AC и AD — наклонные,
BC и BD — их проекции,
Так как AB — перпендикуляр к прямой a, то треугольники ABC и ABD — прямоугольные.
По теореме Пифагора AC²=AB²+BC² и AD²=AB²+BD².
Отсюда, AB²=AC²-BC² и AB²=AD²-BD².
Приравнивая правые части равенств, имеем: AC²-BC²=AD²-BD².
Так как BC>BD, то и BC²>BD².
Значит, и AC²>AD². А так как AC>0 и AD>0, то AC>AD.
Что и требовалось доказать.
И обратно: б о льшей наклонной соответствует б о льшая проекция.
Видео:Геометрия 8. Урок 10 - Теорема Пифагора. Наклонная и проекция.Скачать

Определение перпендикуляра и наклонной
1) Определение перпендикуляра и наклонной.
Пусть дана плоскость и не лежащая на ней точка.
· Отрезок прямой, перпендикулярной плоскости, соединяющий данную точку с точкой на плоскости называется перпендикуляром из данной точки к данной плоскости.
· Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
· Любой отрезок, соединяющий данную точку с точкой на плоскости и не являющийся перпендикуляром к плоскости, называется наклонной.
· Конец отрезка, лежащий в плоскости, называется основанием наклонной.
На рисунке из точки А проведены к плоскости α перпендикуляр АВ и наклонная АС. Точка В — основание перпендикуляра, точка С — основание наклонной, ВС — проекция наклонной АС на плоскость α.
2) Доказательство того, что перпендикуляр корочек наклонной
На рисунке 2 изображена плоскость α, перпендикуляр к ней AO, наклонная AB, а также показан отрезок BO, соединяющий основания наклонной и перпендикуляра. Отрезки AO, BO и AB образуют ΔAOB.
Рассмотрим ΔAOB, из определения перпендикуляра следует, что он прямоугольный. Перпендикуляр AO является катетом этого треугольника, а наклонная AB – его гипотенузой. Катет прямоугольного треугольника всегда меньше его гипотенузы (по теореме Пифагора), следовательно, перпендикуляр всегда короче наклонной.
3) Определение проекции
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
Отрезок BO на рисунке 2 – является проекцией наклонной AB.
4) Теорема о сравнительной длине наклонных и их проекций
А) Любая наклонная больше своей проекции.
Вновь рассмотрим ΔAOB, изображенный на рис. 2, из определения перпендикуляра следует, что он прямоугольный. Проекция BO является катетом этого треугольника, а наклонная AB – его гипотенузой, т. к. катет прямоугольного треугольника всегда меньше его гипотенузы, следовательно, проекция наклонной на плоскость всегда короче самой наклонной.
Б) Равные наклонные имеют равные проекции
Доказательство: Рассмотрим треугольники AOB и AOD, они равны, т. к. равны их гипотенузы AB и AD, и углы AOB и AOD (они прямые), а сторона AO у них общая. Из равенства треугольников следует и равенство их сторон BO = OD, что и требовалось доказать.
В) Если проекции наклонных равны, то и наклонные равны. Доказывается аналогично утверждению Б.
Г) Большей наклонной соответствует большая проекция.
Рассмотрим прямоугольные треугольники AOB и AOD, AB > AD.


Но так как AB > AD => AB2 > AD2 => 

=> BO > DO. Что и требовалось доказать.
Д) Из двух наклонных больше та, у которой проекция больше. Доказывается аналогично Г.
📽️ Видео
Наклонная, проекция, перпендикуляр. 7 класс.Скачать

Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Геометрия 10 класс Атанасян №138 Как найти наклонную и проекцию если известен перпендикуляр и уголСкачать

Наклонная, проекция, перпендикуляр и их свойства. Практическая часть. 7 класс.Скачать

Наклонная, проекция, перпендикуляр и их свойства. 7 класс.Скачать

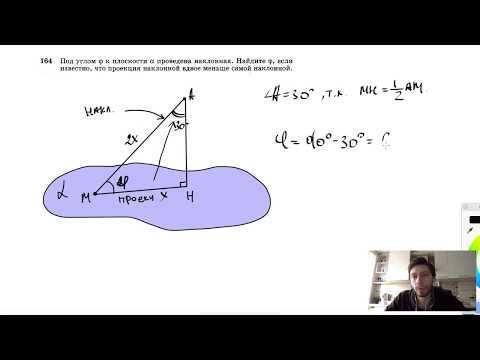
№164. Под углом φ к плоскости α проведена наклонная. Найдите φ, если известно, чтоСкачать
Перпендикуляр и наклонная в пространстве. Практическая часть. 10 класс.Скачать

Свойства проекций катетов | Геометрия 8-9 классыСкачать

Построение треугольника в трёх проекцияхСкачать

Геометрия 10 класс (Урок№10 - Перпендикуляр и наклонные.)Скачать

урок №29 Перпендикуляр, наклонная и проекция наклонной 7 классСкачать

№138. Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которымиСкачать

Стереометрия "с нуля" Урок 6 Перпендикуляр и наклонная к плоскостиСкачать

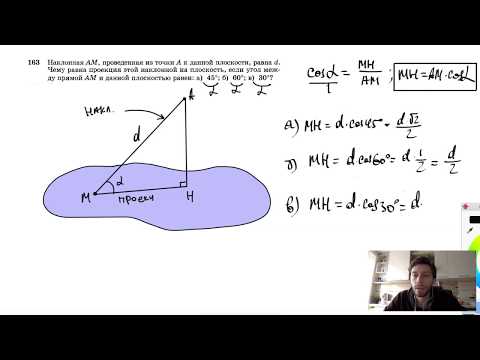
№163. Наклонная АМ, проведенная из точки А к данной плоскости, равна d. Чему равна проекцияСкачать
ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Урок 87. Движение по наклонной плоскости (ч.1)Скачать








