Задача о построении треугольника по заданным биссектрисам. По существу, классическими задачами на построение являются также и задачи, связанные с построением треугольника.
Легко построить треугольник по трем сторонам, чуть сложнее сделать это, если даны три его медианы или три высоты. Самый трудный случай возникает для трех данных биссектрис.
Эта задача трудна даже для равнобедренного треугольника, т.е. тогда, когда две биссектрисы совпадают (если равны все три биссектрисы, то задача легко решается).
АЕ, BD — биссектрисы треугольника
Пусть в равнобедренном треугольнике АВС известны длины биссектрис АЕ и BD АЕ =а, BD = Ь.
Угол при основании треугольника обозначим а. Треугольник АВС будет построен, как только будет найдено значение какой-либо тригонометрической функции угла а. Пусть sin а = х. Наша цель показать, что не для каждого треугольника отрезок х можно построить с помощью циркуля и линейки.
Найдем площадь треугольника АВС двумя способами:
Хдавс = S MCE + аве =-a-2b- ctg 2а • sin 2а + — ? а • sin а • . .
1 Фердинанд Карл Луис Линдеманн (1852-1939) — немецкий математик, профессор Кенигсбергского (с 1883 г.) и Мюнхенского (с 1893 г.) университетов.
Отсюда получаем уравнение:
sin 2a a sin 2a sin 2a
Пусть — = k; разделив обе части уравнения на (явно ненулевое) число ——,
получим уравнение с параметром к:
2 ? cos 2a • к — cos 2a • sin a + sina.
2(l-2sin 2 a)^ = (1-2sin 2 a)sin a + sin a.
При нашем обозначении x = sin a получаем:
2Л( 1 — 2x 2 ) = 2x( 1 — 2x 2 ) + x,
4x 3 — 4Ax 2 -3x + 2k.
При к = 3 получаем:
4у 3 — 12у 2 -3у + 6.
Простым перебором вариантов можно убедиться, что у этого многочлена нет рациональных корней. По теореме Вантцеля его корни нельзя выразить в квадратных радикалах через коэффициенты уравнения, а это значит, что равнобедренный треугольник с соотношением биссектрис 3 : 1 построить с помощью циркуля и линейки нельзя.
При соотношении биссектрис 1 : 3 многочлен:
12у 3 -4у 2 -9у + 2
также не имеет рациональных корней. Его тоже, используя только циркуль и линейку, построить нельзя.
Задача о построении треугольника по трем биссектрисам с помощью циркуля и линейки в общем случае неразрешима.
Отметим, что невозможность построения связана с ограничением на инструменты. Все три основные задачи древности неразрешимы, если использовать инструменты богов: циркуль и линейку без делений. Но стоит лишь чуть приземлить инструментарий, а именно нанести на линейку всего одно деление, как ситуация меняется.
С помощью циркуля и линейки с делением можно и куб удвоить, и трисектрису построить, и начертить правильный семиугольник.
Рассмотрим для примера построение трисектрисы.
Сначала отметим, что прямой угол делится на три части с помощью циркуля и обычной, «божественной» линейки без делений. Тупой угол можно представить в виде суммы прямого и острого угла. Разделив этот острый угол на три части и прибавим к нему треть прямого (угол в 30°), мы получим одну третью исходного тупого угла. Таким образом, достаточно научиться строить трисектрису лишь острых углов.
Итак, пусть дан острый угол АОВ = а, и нам нужно разделить его на три равные части. В нашем распоряжении есть линейка с делением; допустим, что расстояние от начала линейки до деления равно а. Построим прямую ОВ, а затем проведем полуокружность с центром в точке О и радиусом, равным а. С помощью линейки с делением через точку А проведем прямую так, чтобы отрезок DE, отсеченный полуокружностью и прямой ОВ, был равен а. Через точку О построим луч ОС, параллельный прямой AD.
Луч ОС — это и есть искомая трисектриса угла АОВ.
Для доказательства соединим точки А и Е с центром О нашей окружности и рассмотрим два треугольника: ODE и ОЕА. Оба треугольника равнобедренные, причем угол при основании треугольника ОЕА в два раза больше угла при основании треугольника ODE.
Видео:Построение биссектрисы в треугольникеСкачать

Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.
Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.
Виды треугольников по углам
Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.
| Остроугольные | Тупоугольные | Прямоугольные |
| Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС. | Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой. | Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный. |
 |  |  |
Виды треугольников по сторонам
Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.
| Разносторонний | Равнобедренный | Равносторонний |
| Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС. | Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС. | Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС. |
 |  |  |
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.
По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.
Биссектриса
Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.
В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD1, EE1 и CC1.
По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.
Высота
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.
На рисунке показаны высоты треугольника АВС: АН1, ВН2 и СН3.
По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.
Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.
При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .
Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.
Составим отношение сторон:
A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF
Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.
Составим отношение сторон:
A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .
Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .
Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24
Теперь найдем CD=AC-AD=54-24=30
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Медианы, биссектрисы и высоты треугольника
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы продолжим рассмотрение элементов треугольника – медиан, биссектрис и высот треугольника.
Вначале дадим определение медианы треугольника и рассмотрим три медианы треугольника. Дадим определение биссектрисы треугольника и рассмотрим три биссектрисы треугольника. Дадим определение высоты треугольника и рассмотрим высоты в произвольном треугольнике и в тупом треугольнике. Далее решим ряд задач с использованием этих элементов.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
💥 Видео
7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Построение треугольника по трём сторонам с помощью циркуля и линейки. 5 классСкачать

Построение биссектрисы углаСкачать

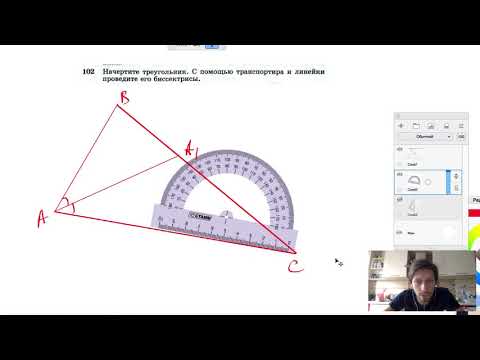
№102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.Скачать
Построение биссектрисы угла. 7 класс.Скачать

Построение медианы в треугольникеСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Биссектрисы треугольника.Скачать

ХОЗБЛОК. Армокаркас для ленточного фундамента 4м * 3 м.Скачать

Построение высоты в треугольникеСкачать

Формула для биссектрисы треугольникаСкачать

Биссектриса треугольника. Построение. 1 частьСкачать

Построение биссектрисы углаСкачать

Найдите биссектрису треугольникаСкачать
Свойство биссектрисы треугольника с доказательствомСкачать

Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать

№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать










