На единичной окружности лежит точка

Геометрия | 5 — 9 классы

На единичной окружности лежит точка м( — 1 / 2 ; корень3 / 2).

Тогда sin угла АОМ равен А)1 / 2 б)корень 3 / 2.

Синус угла в единичной окружности — это ордината

Е. , sin(∠AOM) = √3 / 2.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Дана окружность с центром о и диаметром аб?

Дана окружность с центром о и диаметром аб.

Точка с лежит на окружность.

Найдите гдадусную меру угла асо, если угол соб равен 96 градусов.

Видео:Как искать точки на тригонометрической окружности.Скачать

Треугольник ABC вписан в окружность с центром в точке О?

Треугольник ABC вписан в окружность с центром в точке О.

Найдите градусную меру угла С треугольника АВС, если угол АОВ равен 153 градуса.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Запишите уравнение окружности проходящей через начало координат и точку А(6 ; 0), если известно, что радиус окружности равен 3(корень из 2), центр лежит на прямой у = х?

Запишите уравнение окружности проходящей через начало координат и точку А(6 ; 0), если известно, что радиус окружности равен 3(корень из 2), центр лежит на прямой у = х.

Видео:Изобразить на единичной окружности точку.Скачать

Точка о — центр окружности угол асв = 48?

Точка о — центр окружности угол асв = 48.

Найти величину угла аов.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Окружность вписаная в ромб, точкой касания делит его сторону в отношении 2 : 3, тогда sin угла ромба равен?

Окружность вписаная в ромб, точкой касания делит его сторону в отношении 2 : 3, тогда sin угла ромба равен?

Видео:Отбор корней по окружностиСкачать

Отрезок прямой АВ — хорда, окружности с центром в точке О?

Отрезок прямой АВ — хорда, окружности с центром в точке О.

Угол АОВ равен 146 гр.

Найдите величину угла между прямой и касательной к окружности, проходящей через точку А.

Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

Найдите величину угла АСВ если величина угла аов равна 130, а окружность с центром в точке О касается сторон угла С в точках А и В?

Найдите величину угла АСВ если величина угла аов равна 130, а окружность с центром в точке О касается сторон угла С в точках А и В.

Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать

В угол С, вписанна окружность с центром в точке О, которая касается сторон угла в точках А и В?

В угол С, вписанна окружность с центром в точке О, которая касается сторон угла в точках А и В.

Угол АОВ равен 33°.

Ответ дайте в градусах.

Видео:45 Где лежат на единичной окружности точки π/4, 3π/4Скачать

Касательная в точках а и в к окружностям с центром о пересекаются под углом 68 найдите аов?

Касательная в точках а и в к окружностям с центром о пересекаются под углом 68 найдите аов.

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Прямая АО перпендикулярно плоскости окружности с центром О?

Прямая АО перпендикулярно плоскости окружности с центром О.

Точка В лежит на окружности.

Найти расстояние от точки А до точки В, если радиус окружности равен 8 см и угол А В О равен 60 градусов.

На этой странице сайта размещен вопрос На единичной окружности лежит точка м( — 1 / 2 ; корень3 / 2)? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Абд равно бцд т. К сумма углов треугольника равна 180 градусов то угол абд будет равен углу цбд а треугольники равны по стороне и двум прилежащим углам соответственно.

∠1 = 180° — 50° = 130°, так как сумма смежных углов равна 180°. ∠1 = ∠3 = 130°, а эти углы соответственные при пересечении прямых b и с секущей n, значитb║c. ∠2 = 180° — 108° = 72° так как эти углы смежные. ∠х = ∠2 = 72° как соответственные при пе..

Извини, времени нет всё решить, но с 1 — ым помогу LL1 = (2a + 5b) / 2 KK1 = ((2a + 5b) / 2 + 2a) / 2 MM1 = ((2a + 5b) / 2 + 5b) / 2 Вроде, так.

Угол. Равный 90°, разделен лучом так, что 3 угла АВL = 2 углам LВС⇒ 3 ∠АВL = 2 ∠LВС⇒ ∠LВС = 3∠АВL : 2⇒ 5∠ABL = 180° ∠ABL = 36° ∠LBC = 90° — 36° = 54° Проверка : 3∠ABL = 3•36° = 108° 2∠LBC = 2•54° = 108° — решение верно.

Решение в приложении.

Abcd параллелограмм ab = X bc = X + 4 2x + 2(x + 4) = 24 2x + 2x + 8 = 24 4x = 24 — 8 4x = 16 x = 4 ab и cd = 4 см bc и ad = 8см.

Δ прямоугольный ? Δ прямоугольный по теореме Пифагора найдем AB : [img = 10] [img = 11] [img = 12] [img = 13] Ответ : [img = 14].

Углы вертикальные . Вобщем 360 градусов.

30, 30, 150, 150 так как получаются вертикальные углы.

В треугольнике АВО ∠В = ∠А = 30⇒∠О = 180 — 60 = 120°⇒ Углы между диагоналями 120°и 60°.

Видео:№168. Двугранный угол равен φ. На одной грани этого угла лежит точка, удаленная на расстояние dСкачать

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

На единичной окружности лежит точка

Введем основные тригонометрические функции.

Пусть радиус-вектор $vec = bar$ точки $M$ образует угол $alpha$ с осью $Ox$ (рис.), причем $x$ и $y$ соответственно абсцисса и ордината конца $M$ вектора, $r$ — его модуль, а величина угла $alpha$ измеряется в градусах или в радианах.

1. Синусом угла $alpha$ (обозначение: $sin alpha$) называется отношение ординаты $y$ (см. рис.) к длине $r$ радиуса-вектора $bar $:

2. Косинусом угла $alpha$ (обозначение: $cos alpha$) называется отношение абсциссы $x$ к длине $r$ радиуса-вектора $bar $:

3. Тангенсом угла $alpha$ (обозначение: $tg alpha$) называется отношение синуса угла $alpha$ к косинусу этого угла:

4. Котангенсом угла $alpha$ (обозначение: $ctg alpha$) называется отношение косинуса угла $alpha$ к синусу этого угла:

5. Секансом угла $alpha$ (обозначение: $sec alpha$) называется величина, обратная $cos alpha$:

6. Косекансом угла $alpha$ (обозначение: $cosec alpha$) называется величина, обратная $sin alpha$:

Замечание 1. Тригонометрические функции (1) — (6) действительно являются функциями только угла $alpha$, т. е. не зависят от длины подвижного радиуса-вектора. Для того чтобы в этом убедиться, достаточно доказать, что если подвижный радиус-вектор $vec$ образует с осью абсцисс данный угол $alpha$, то отношения $frac$ и $frac$ не зависят от длины радиуса-вектора.

Замечание 2. Из определения $tg alpha$ и $ctg alpha$ следует, что

$tg alpha = frac$, (7)
$ctg alpha = frac$. (8)

Соотношения (7) и (8) можно было бы принять в качестве определений для $tg alpha$ и $ctg alpha$.

Замечание 3. Аналогично получаем

$sec alpha = frac$,(9)
$cosec alpha = frac$ (10).

Соотношения (9) и (10) можно было бы также принять в качестве определений для $sec alpha$ и $cosec alpha$.

Замечание 4. Во всех определениях (1) — (6) предполагаем, что соответствующие отношения существуют (имеют смысл). Например, $tg alpha$ имеет смысл, если $cos alpha neq 0, ctg alpha$ имеет смысл, если $sin alpha neq 0$, и т.д. Поскольку (замечание 1) тригонометрические функции (1) — (6) угла $alpha$ не зависят от длины подвижного радиуса-вектора, то в качестве радиуса-вектора можно брать вектор с длиной, равной единице $(| vec| = r = 1)$. Такой вектор называют единичным радиусом-вектором. В случае единичного радиуса-вектора формулы для основных тригонометрических функций запишутся так (рис.):

$begin sin alpha = y, cos alpha = x \ tg alpha = frac, ctg alpha = frac \ sec alpha = frac, cosec alpha = frac end$. (11)

Формулы для $tg alpha$ и $ctg alpha$ остались прежними (см. (7) и (8)), а формулы для остальных основных тригонометрических функций приняли более простой вид (см. (1), (2), (9) и (10)). Следовательно, синус и косинус угла а равны соответственно ординате и абсциссе конца подвижного единичного радиуса-вектора. Конец этого единичного радиуса-вектора при изменении угла а от $0^$ до $360^$ опишет окружность, называемую единичной окружностью (рис.). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов. Осью тангенсов называется перпендикуляр, восставленный в точке $A$ к неподвижному радиусу-вектору $bar$. Положительное и отрицательное направления на оси тангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси ординат (рис.). Рассмотрим угол $alpha = angle AOM$ и введем понятие соответствующей точки оси тангенсов.

а) Если точка $M$ единичной окружности лежит справа от оси ординат, то соответствующей ей точкой оси тангенсов назовем точку $M_$ (точку пересечения продолжения $MO$ с осью тангенсов, рис а.

б) Если точка $M$ единичной окружности лежит слева от оси ординат, то соответствующей ей точкой сси тангенсов назовем точку $M_$ (точку пересечения продолжения $MO$ с ссыо тангенсов, рис. б.

Заметим, что тангенс угла а численно равен ординате $y_$ (рис.) соответствующей точки сси тангенсов, т. е. всегда $tg alpha — y_$. Докажем это для углов первых двух четвертей:

1) $0^ leq alpha < 90^$ (рис. a), $tg alpha = frac<y_> = y_ geq 0$, где $y_$ — ордината точки $M_$.
2) $90^ < alpha leq 180^$ (рис. б). $tg alpha = frac<y_><x_> leq 0$, где $x_$ и $y_$ — абсцисса и ордината точки $M$. Из подобия прямоугольных треугольников $OMM_$ и $OM_A$ имеем

Следовательно, $tg alpha = frac<y_><x_> = y_ leq 0$.

Заметим еще следующее:
а) если точка $M$ лежит на оси ординат (например, $alpha = 270^$), то соответствующей ей точки сси тангенсов не существует, но при этом и $tg alpha$ также не существует;
б) в рассмотренных случаях 1)-2) мы брали угол $alpha$ в пределах от $0^$ до $360^$, но в наших рассуждениях ничего не изменится, если мы будем предполагать угол $alpha$ любым.

Осью котангенсов называется перпендикуляр, восставленный в точке В (конец радиуса-вектора $bar $, образующего с осью $Ox$ угол, равный $90^$) к оси ординат. Положительное и отрицательное направления на оси котангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси абсцисс (рис.). Введем понятие соответствующей точки оси котангенсов.

а) Если точка $M$ единичной окружности лежит над осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку $M_$ (точку пересечения продолжения $OM$ с осью котангенсов, рис. а).

б) Если точка $M$ единичной окружности лежит под осью абсцисс, то соответствующей ей точкой сси котангенсов назовем точку (точку пересечения продолжения $MO$ с осью котангенсов, рис. б).

Аналогично предыдущему можно получить, что котангенс угла $alpha$ равен абсциссе $x_$ соответствующей точки оси котангенсов, т. е. $ctg alpha = x_$. Если точка $M$ лежит на оси абсцисс (например, $alpha — 180^$), то соответствующей ей точки оси котангенсов не существует, но при этом и $ctg alpha$ также не существует.

🔥 Видео

Числовая окружностьСкачать

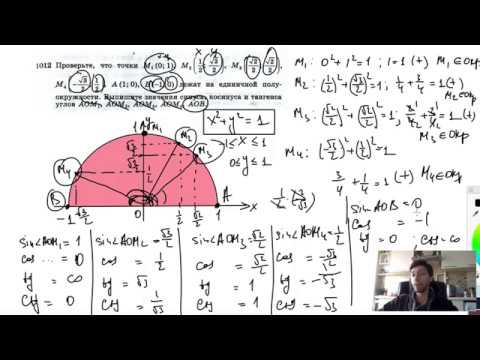
№1012. Проверьте, что точки М1(0; 1), M2(½;√3/2), M3(√2/2; √2/2)Скачать

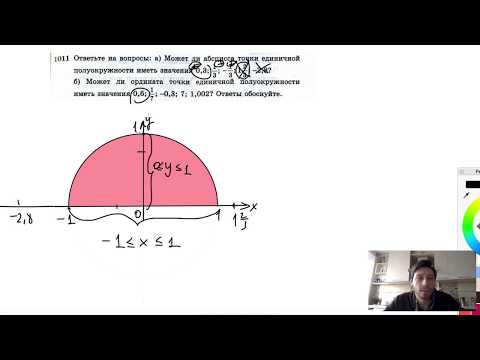
№1011. Ответьте на вопросы: а) Может ли абсцисса точки единичной полуокружности иметь значения 0,3Скачать

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Точки на числовой окружностиСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

46 Где расположены на единичной окружности точки π/3,π/6 и другиеСкачать