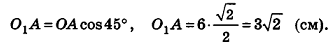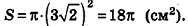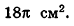Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
- Некоторые свойства пирамиды
- Виды пирамид
- Многогранники. Виды многогранников и их свойства
- Понятие многогранника, виды многогранников в геометрии
- Призма и её свойства
- Пирамида
- Правильный многогранник: виды и свойства многогранников
- Гексаэдр и его свойства
- Тетраэдр
- Октаэдр и его свойства
- Додекаэдр
- Икосаэдр
- Полуправильные многоугольники
- Звёздчатые многогранники
- Многогранник — виды, свойства и формулы с примерами решения
- Определение многогранника
- Построение многогранников и их простейших сечений
- Пример №1
- Пример №2
- Пример №3
- Многогранные углы и многогранники
- Пример №4
- Многогранники в геометрии
- Многогранники в высшей математике
- Призмы
- Многогранники и их виды с различных сторон
- Площадь поверхности призмы
- Площадь боковой поверхности прямой призмы
- Площадь полной поверхности призмы
- Сечение призмы плоскостью
- Пирамида
- Площадь боковой поверхности правильной пирамиды
- Сечение пирамиды плоскостью. Усечённая пирамида
- Многогранники и их изображения
- Многогранники
- Куб, параллелепипед
- Призма и пирамида
- Аксиомы стереометрии
- Пример №9
- Пример №10
- Пример №11
- Пример №12
- Следствия из аксиом
- Построение сечений многогранников плоскостью
- Пример №13
- Пример №14
- Подробное построение сечений многогранников
- Пример №15
- Пример №16
- Пример №17
- Пример №18
- Пример №19
- Пример №20
- Пример №21
- Пример №22
- Многограники в геометрии
- Двугранные и многогранные углы. многогранник
- Двугранный угол
- Трехгранный и многогранный углы
- Правила определения понятий
- Пирамида
- Пирамида и ее элементы
- Правильная пирамида
- Нахождение расстояния от точки до плоскости боковой грани пирамиды
- Некоторые виды пирамид
- Сечения многогранников
- Секущая плоскость и сечение. Сечения призмы
- Сечения пирамиды. Усеченная пирамида
- Построение сечений многогранников
- Построение точки X пересечения прямой АВ с плоскостью основания многогранника
- Правильные многогранники
- Виды правильных многогранников
- Полуправильные многогранники. Другие виды многогранников
- Справочный материал
- Двугранные и многогранные углы
- Многогранники
- Призмы
- Пирамиды
- Историческая справка
- Тела вращения
- Цилиндр
- Поверхности и тела вращения
- Пример №223
- Виды определений
- Конус
- Конус и его элементы
- Сечения конуса. Усеченный конус
- Пример №224
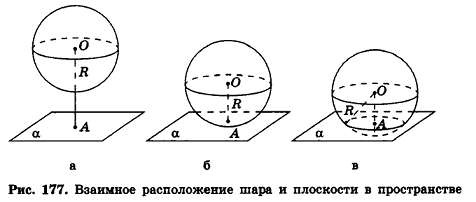
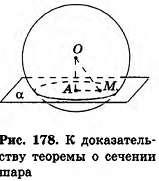
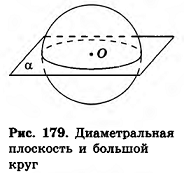
- Шар и сфера
- Пример №225
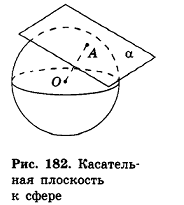
- Касательная плоскость к сфере
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

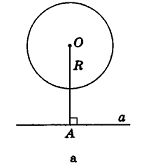
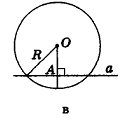
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
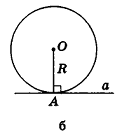
2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное.
Видео:Геометрия 10 класс (Урок№13 - Многогранник.)Скачать

Виды пирамид
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Видео:27. Понятие многогранникаСкачать

Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Многогранники. Виды многогранников и их свойства
Многогранники не только занимают видное место в геометрии, но и встречаются в повседневной жизни каждого человека. Не говоря уже об искусственно созданных предметах обихода в виде различных многоугольников, начиная со спичечного коробка и заканчивая архитектурными элементами, в природе также встречаются кристаллы в форме куба (соль), призмы (хрусталь), пирамиды (шеелит), октаэдра (алмаз) и т. д.
Видео:Урок 03. Многогранники в стереометрииСкачать

Понятие многогранника, виды многогранников в геометрии
Геометрия как наука содержит раздел стереометрию, изучающую характеристики и свойства объёмных фигуры. Геометрические тела, стороны которых в трёхмерном пространстве образованы ограниченными плоскостями (гранями), носят название «многогранники». Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.
Тем не менее у всех многогранников есть общие свойства:
- Все они имеют 3 неотъемлемых компонента: грань (поверхность многоугольника), вершина (углы, образовавшиеся в местах соединения граней), ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).
- Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.
- Выпуклость означает, что тело полностью расположено только по одну сторону плоскости, на которой лежит одна из граней. Правило применимо ко всем граням многогранника. Такие геометрические фигуры в стереометрии называют термином выпуклые многогранники. Исключение составляют звёздчатые многогранники, которые являются производными правильных многогранных геометрических тел.
Многогранники можно условно разделить на:
- Виды выпуклых многогранников, состоящих из следующих классов: обычные или классические (призма, пирамида, параллелепипед), правильные (также называемые Платоновыми телами), полуправильные (второе название – Архимедовы тела).
- Невыпуклые многогранники (звёздчатые).
Видео:10 класс, 27 урок, Понятие многогранникаСкачать

Призма и её свойства
Стереометрия как раздел геометрии изучает свойства трёхмерных фигур, виды многогранников (призма в их числе). Призмой называют геометрическое тело, которое имеет обязательно две совершенно одинаковые грани (их также называют основаниями), лежащие в параллельных плоскостях, и n-ое число боковых граней в виде параллелограммов. В свою очередь, призма имеет также несколько разновидностей, в числе которых такие виды многогранников, как:
- Параллелепипед — образуется, если в основании лежит параллелограмм — многоугольник с 2 парами равных противоположных углов и двумя парами конгруэнтных противоположных сторон.
- Прямая призма имеет перпендикулярные к основанию рёбра.
- Наклонная призма характеризуется наличием непрямых углов (отличных от 90) между гранями и основанием.
- Правильная призма характеризуется основаниями в виде правильного многоугольника с равными боковыми гранями.
Основные свойства призмы:
- Конгруэнтные основания.
- Все рёбра призмы равны и параллельны по отношению друг к другу.
- Все боковые грани имеют форму параллелограмма.
Видео:Пересечение многогранников. Пирамида с призматическим вырезом.Скачать

Пирамида
Пирамидой называют геометрическое тело, которое состоит из одного основания и из n-го числа треугольных граней, соединяющихся в одной точке – вершине. Следует отметить, что если боковые грани пирамиды представлены обязательно треугольниками, то в основании может быть как треугольный многоугольник, так и четырёхугольник, и пятиугольник, и так до бесконечности. При этом название пирамиды будет соответствовать многоугольнику в основании. Например, если в основании пирамиды лежит треугольник – это треугольная пирамида, четырёхугольник – четырёхугольная, и т. д.
Пирамиды – это конусоподобные многогранники. Виды многогранников этой группы, кроме вышеперечисленных, включают также следующих представителей:
- Правильная пирамида имеет в основании правильный многоугольник, и высота ее проектируется в центр окружности, вписанной в основание или описанной вокруг него.
- Прямоугольная пирамида образуется тогда, когда одно из боковых рёбер пересекается с основанием под прямым углом. В таком случае это ребро справедливо также назвать высотой пирамиды.
- В случае если все боковые рёбра пирамиды конгруэнтны (одинаковой высоты), то все они пересекаются с основанием под одним углом, а вокруг основания можно прочертить окружность с центром, совпадающим с проекцией вершины пирамиды.
- Если в основании пирамиды лежит правильный многоугольник, то все боковые рёбра конгруэнтны, а грани являются равнобедренными треугольниками.
Видео:Многогранник. 11 класс.Скачать

Правильный многогранник: виды и свойства многогранников
В стереометрии особое место занимают геометрические тела с абсолютно равными между собой гранями, в вершинах которых соединяется одинаковое количество рёбер. Эти тела получили название Платоновы тела, или правильные многогранники. Виды многогранников с такими свойствами насчитывают всего пять фигур:
Своим названием правильные многогранники обязаны древнегреческому философу Платону, описавшему эти геометрические тела в своих трудах и связавшему их с природными стихиями: земли, воды, огня, воздуха. Пятой фигуре присуждали сходство со строением Вселенной. По его мнению, атомы природных стихий по форме напоминают виды правильных многогранников. Благодаря своему самому захватывающему свойству – симметричности, эти геометрические тела представляли большой интерес не только для древних математиков и философов, но и для архитекторов, художников и скульпторов всех времён. Наличие всего лишь 5 видов многогранников с абсолютной симметрией считалось фундаментальной находкой, им даже присуждали связь с божественным началом.
Видео:Лекция № 7. Многогранники. Виды многогранников. Основные позиционные задачиСкачать

Гексаэдр и его свойства
В форме шестигранника преемники Платона предполагали сходство со строением атомов земли. Конечно же, в настоящее время эта гипотеза полностью опровергнута, что, однако, не мешает фигурам и в современности привлекать умы известных деятелей своей эстетичностью.
В геометрии гексаэдр, он же куб, считается частным случаем параллелепипеда, который, в свою очередь, является разновидностью призмы. Соответственно и свойства куба связаны со свойствами призмы с той лишь разницей, что все грани и углы куба равны между собой. Из этого вытекают следующие свойства:
- Все рёбра куба конгруэнтны и лежат в параллельных плоскостях по отношению друг к другу.
- Все грани – конгруэнтные квадраты (всего в кубе их 6), любой из которых может быть принят за основание.
- Все межгранные углы равны 90.
- Из каждой вершины исходит равное количество рёбер, а именно 3.
- Куб имеет 9 осей симметрии, которые все пересекаются в точке пересечения диагоналей гексаэдра, именуемой центром симметрии.
Видео:Многогранники. Геометрия 11 класс.Скачать

Тетраэдр
Тетраэдр – это четырёхгранник с равными гранями в форме треугольников, каждая из вершин которых является точкой соединения трёх граней.
Свойства правильного тетраэдра:
- Все грани тетраэда – это равносторонние треугольники, из чего следует, что все грани четырёхгранника конгруэнтны.
- Так как основание представлено правильной геометрической фигурой, то есть имеет равные стороны, то и грани тетраэдра сходятся под одинаковым углом, то есть все углы равны.
- Сумма плоских углов при каждой из вершин равняется 180, так как все углы равны, то любой угол правильного четырёхгранника составляет 60.
- Каждая из вершин проецируется в точку пересечения высот противоположной (ортоцентр) грани.
Видео:Видеоурок по математике "Понятие правильного многогранника"Скачать

Октаэдр и его свойства
Описывая виды правильных многогранников, нельзя не отметить такой объект, как октаэдр, который визуально можно представить в виде двух склеенных основаниями четырёхугольных правильных пирамид.
- Само название геометрического тела подсказывает количество его граней. Восьмигранник состоит из 8 конгруэнтных равносторонних треугольников, в каждой из вершин которого сходится равное количество граней, а именно 4.
- Так как все грани октаэдра равны, равны и его межгранные углы, каждый из которых равняется 60, а сумма плоских углов любой из вершин составляет, таким образом, 240.
Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Додекаэдр
Если представить, что все грани геометрического тела представляют собой правильный пятиугольник, то получится додекаэдр – фигура из 12 многоугольников.
- В каждой вершине пересекаются по три грани.
- Все грани равны и имеют одинаковую длину рёбер, а также равную площадь.
- У додекаэдра 15 осей и плоскостей симметрии, причём любая из них проходит через вершину грани и середину противоположного ей ребра.
Видео:Математика 10 класс. Многогранники.Скачать

Икосаэдр
Не менее интересная, чем додекаэдр, фигура икосаэдр представляет собой объёмное геометрическое тело с 20 равными гранями. Среди свойств правильного двадцатигранника можно отметить следующие:
- Все грани икосаэдра — равнобедренные треугольники.
- В каждой вершине многогранника сходится пять граней, и сумма смежных углов вершины составляет 300.
- Икосаэдр имеет так же, как и додекаэдр, 15 осей и плоскостей симметрии, проходящих через середины противоположных граней.
Видео:Правильные и полуправильные многогранникиСкачать

Полуправильные многоугольники
Кроме Платоновых тел, в группу выпуклых многогранников входят также Архимедовы тела, которые представляют собой усечённые правильные многогранники. Виды многогранников данной группы обладают следующими свойствами:
- Геометрические тела имеют попарно равные грани нескольких типов, например, усечённый тетраэдр имеет так же, как и правильный тетраэдр, 8 граней, но в случае Архимедова тела 4 грани будут треугольной формы и 4 — шестиугольной.
- Все углы одной вершины конгруэнтны.
Видео:МногогранникиСкачать

Звёздчатые многогранники
Представители необъёмных видов геометрических тел – звёздчатые многогранники, грани которых пересекаются друг с другом. Они могут быть образованы путём слияния двух правильных трёхмерных тел либо в результате продолжения их граней.
Таким образом, известны такие звёздчатые многогранники, как: звёздчатые формы октаэдра, додекаэдра, икосаэдра, кубооктаэдра, икосододекаэдра.
Видео:10 класс, 30 урок, ПризмаСкачать

Многогранник — виды, свойства и формулы с примерами решения
Содержание:
Известно, что фигуры делятся на плоские и пространственные, в зависимости от того, расположена фигура только на плоскости или в пространстве. До сих пор мы на уроках геометрии, в основном, изучали свойства плоских фигур. В конце 9 класса мы рассмотрели свойства некоторых пространственных фигур: призмы, пирамиды, цилиндра, конуса и шара (рис.1). В планиметрии изучают свойства плоских фигур, а в стереометрии — свойства пространственных фигур. Стереометрия (от греческого «stereos» — «пространственный», «metreo» — «измеряю»).
Предметы, изображенные на рисунке 2, как символы пространственных тел, дают представление о них. Все предметы окружающего нас мира имеют три измерения, их форма похожа на какую-нибудь геометрическую фигуру. Вы познакомились с такими фигурами в конце 9 класса. Теперь начинаем системное изучение курса стереометрии. Сначала вкратце напомним некоторые сведения об элементах пространственных фигур.
Видео:ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Определение многогранника
Многогранник — это пространственное тело, ограниченное плоскими многоугольниками.
Плоские многоугольники называют гранями многогранника, их вершины — вершинами многогранника, а стороны — ребрами многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называют диагональю многогранника (рис. 3).
Границу многогранника называют его поверхностью. Многогранник делит пространство на две части. Одну из них, бесконечную, называют внешней областью, а ограниченную часть внутренней областью многогранника.
Если многогранник расположен по одну сторону от плоскости, проходящей через любую его грань, то многогранник называют выпуклым многогранником. Например, куб — выпуклый многогранник. На рисунке 4 изображен многогранник, не являющийся выпуклым. Позже мы будем изучать простейшие многогранники: призмы и пирамиды.
Многогранник, две грани которого, являются равными многоугольниками, а остальные — параллелограммами, называют призмой (рис. 5). Равные грани называют основаниями, а параллелограммы боковыми гранями многогранника (рис. 6).
По числу сторон в основании многогранники разделяют на треугольные, четырехугольные и т.д. n-угольные призмы.
На рисунке 5.а изображена треугольная призма 
Если боковая грань призмы перпендикулярна основанию, то ее называют прямой призмой, если не перпендикулярна, то наклонной призмой.
Если основания прямой призмы являются правильными многоугольниками, то его называют правильной (рис. 8).
Призма, основанием которой является параллелограмм, называют параллелепипедом (рис. 9). Параллелепипеды, как и призмы, могут быть прямыми и наклонными. Прямой параллелепипед с прямоугольным основанием называют прямоугольным параллелепипедом (рис. 10). Ясно, что все грани прямоугольного параллелепипеда будут прямоугольниками.
Три ребра прямоугольного параллелепипеда, исходящие из одной вершины, называют его измерениями.
Прямоугольный параллелепипед с равными измерениями называется кубом. Ясно, что гранями куба являются равные квадраты.
По числу сторон основания различают треугольные, четырехугольные и т.д. n-угольные пирамиды.
На рисунке 13 изображена треугольная, а на рисунке 14-четырехугольная пирамида.
Если основанием пирамиды является правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, перпендикулярен любой прямой, проведенной в плоскости основания через этот центр, то сс называют правильной пирамидой.
Высоту боковой грани, опущенную из вершины правильной пирамиды, называют апофемой. На рисунке 14 изображена правильная пирамида APQRS. Отрезок АВ является апофемой этой пирамиды.
Теорема 1.1. В правильной пирамиде: а) боковые грани; б) боковые ребра; в) апофемы равны между собой.
Доказательство: Пусть 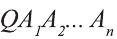
а) Отрезки 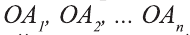
Так как в прямоугольных треугольниках 
б) Так как боковые ребра правильной пирамиды 
Следовательно, боковые грани пирамиды равны по трем сторонам.
в) Так как боковые грани правильной пирамиды равны, то апофемы, проведенные из вершины Q, также равны между собой.
Следовательно, в правильной пирамиде апофемы равны между собой.□
Теорема 1.2. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на ее апофему.
Доказательство: Пусть 
Построение многогранников и их простейших сечений
При решении геометрических задач очень важно построить правильный чертеж. Часто считают правильный чертеж — «половиной решения». Правильное построение стереометрических чертежей считается достаточно сложной, ответственной, а иногда и трудной работой, так как стереометрические фигуры имеют три измерения и их нужно изобразить на плоскости, на странице тетради. Неправильный чертеж может привести к неверному решению или к тупику.
Построение призмы выполняют в следующем порядке (рис. 11). Сначала строят одно из оснований в виде многоугольника. Затем из каждой вершины многоугольника проводят параллельные и равные друг другу отрезки, то есть образующие призмы. Концы этих отрезков последовательно соединяют. Получают второе основание призмы. На чертеже невидимые ребра призмы чертят штрих-пунктирной линией.
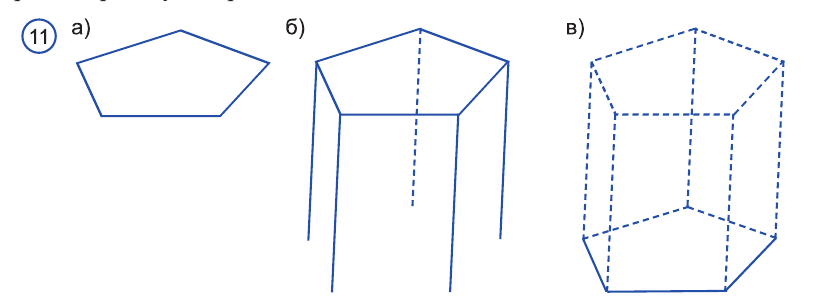
Правильный чертеж можно построить только при правильном представлении взаимного расположения пространственных геометрических фигур. Если одной из пространственных фигур является многогранник, а другой плоскость, то необходимо построить их сечение. Займемся построением таких сечений.
Пусть многогранник пересекает некоторая плоскость. Геометрическая фигура, являющаяся многоугольником, вершины которого — это точки пересечения многогранника и плоскости, называют сечением многогранника.
Секущая плоскость пересекает поверхность многогранника по отрезкам, а сечение многогранника состоит из одного или нескольких многоугольников. На рисунке 13 изображено сечение пятиугольной призмы, являющееся семиугольником. Сечение на рисунке 14, полученное пересечением рамы плоскостью, состоит из двух четырехугольников.
Чтобы изобразить сечение многогранника, нужно отметить общие точки его граней и секущей плоскости.
Пример №1
Построим сечение треугольной пирамиды QABC, которая пересекает ее ребра АВ, AQ и CQ в точках К, L М соответственно (рис. 15).
Решение:
Построение. Секущая плоскость а имеет с гранью AQB пирамиды две общие точки: К и L. Следовательно секущая плоскость пересекает эту грань по отрезку KL.
Аналогично, так как секущая плоскость а имеет с гранью AQC пирамиды две общие точки М и L, поэтому она пересекает эту грань по отрезку ML.
Секущая плоскость а имеет с гранью ABC пирамиды одну общую точку К. Найдем точку, в которой эта плоскость пересекается с ребром ВС. Продолжив прямые LMи АС, принадлежащие этой плоскости, найдем их точку пересечения X. Точка X лежит также в плоскостях AQC и ABC.
Секущая плоскость а имеет с гранью ABC пирамиды две общие точки: К vi X. Тогда секущая плоскость пересекает эту грань по отрезку КХ.
Точка N пересечения прямой КХ и ребра ВС также принадлежит плоскости а.
Следовательно, плоскость а пересекает грань ABC по отрезку KN, а грань BQC по отрезку MN.
Четырехугольник KLMN является сечением пирамиды плоскостью а. Каждый из отрезов KL и KN называют следом плоскости а на гранях ABQ и ABC соответственно.
Пример №2
Построим сечение треугольной пирамиды OKLMN, полученное пересечением плоскости b с ребром пирамиды OL в точке А и прямой к, лежащей в основании пирамиды KLMN (рис. 16).
Решение:
Построение. Найдем точку пересечения прямых LM и к. Так как эта точка лежит на прямой к, то она принадлежит и плоскости р. Подобно этому, так как эта точка лежит на прямой LM, то она принадлежит и грани LOM. Точка А принадлежит обеим этим плоскостям. Поэтому плоскость Р псрссскаст плоскость LOM по прямой АХ, а грань LOM по отрезку АВ. Точка В является точкой пересечения прямых АХ и ОМ.
Точно также, определяем точки У и D пересечения плоскости р и ребра OLK и отрезка AD. Затем определяем точки Z и С и прямые DC и ВС. В результате, полученный четырехугольник ABCD является искомым сечением.
Пример №3
Точки А, В и С лежат на разных ребрах четырехугольной призмы. Найдем сечение призмы плоскостью ABC (рис. 17).
Решение:
Искомое сечение зависит от того, на каких ребрах четырехугольной призмы и как расположены точки А, В и С. На рисунке 17 изображен наиболее простой случай, когда точки А, В и С расположены на ребрах, исходящих из одной вершины.
Построение сечения в случае, изображенном на рисунке 18, считается более сложным. Оставшиеся случаи сечений приведены на рисунках 19 и 20. Как видите, сечение может быть треугольником, четырехугольником, пятиугольником и шестиугольником. Построение этих сечений выполните самостоятельно.
Многогранные углы и многогранники
С двугранным углом вы познакомились в 10 классе. Геометрическую фигуру, состоящую из двух полуплоскостей (грани) а и b с общей их ограничивающей прямой АВ (ребро) называют двугранным углом (рис. 1) и обозначают (а b).
Начертим лучи РR и РQ, проходящие через произвольную точку Р на рёбре двугранного угла и перпендикулярные ему. Угол 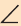
Двугранные углы также как и плоские углы делят по величине на острые, прямые и тупые (рис. 3). Также как и плоские углы двугранные углы могут быть смежными и вертикальными (рис. 4).
Полуплоскость, делящую двугранный угол на два равных двугранных угла, называют биссектором (рис. 5).
Пример №4
Из точек А и В, лежащих на гранях двугранного угла, линейный угол которого равен 60°, к его рёбру проведены перпендикуляры АА1 и ВВ1 (рис. 6). Найдите длину отрезка АВ, если АА1 = 12, ВВ1 = 10 и А1В1 = 13.
Решение:
Проведем прямые 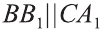
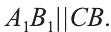
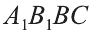
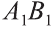
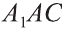
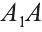
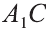
Следовательно, треугольник АВС — прямоугольный.
По теореме косинусов:
А по теореме Пифагора:
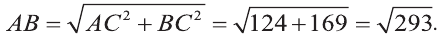
В пространстве три исходящих из одной точки луча a, b и с образуют три плоских угла (ab), (bс) и (ас) (рис.7). Фигуру (abc), полученную из этих плоских углов, называют трёхгранным углом.
Плоские углы трёхгранного угла называют его гранями, их стороны
— рёбрами, а общую вершину — вершиной трёхгранного угла.
Двугранные углы, образованные гранями трехгранного угла, называют двугранными углами трёхгранного угла.
Три плоских угла (ab), (bс) и (ас) называют также плоскими углами трёхгранного угла.
Плоские углы трёхгранного угла обозначают соответственно 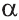
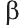
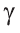
и сумма плоских углов трёхгранного угла меньше 360 о :
.
Аналогично определяется понятие многогранного угла (рис. 9).
Многогранники в геометрии
Если вы заметили, то до сих пор мы изучали в качестве пространственных фигур свойства ряда тел, в частности многогранников. Эти пространственные фигуры называются телами, поскольку их можно представить в виде части пространства, занятой каким-либо телом и ограниченной поверхностью. Напомним некоторые понятия, касающиеся многогранников.
Многогранником называют тело, ограниченное плоскими многоугольниками (рис. 10).
Если многоугольник расположен по одну сторону от плоскости каждой грани, то его называют выпуклым многогранником. На рисунке 10 изображён выпуклый, а на рисунке 11 не выпуклый многогранник. Обозначим число граней произвольного выпуклого многогранника Y, число его вершин U, число его рёбер Q. Заполним следующую таблицу для известных нам многогранников:
Из таблицы получаем, что 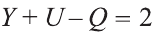
Теорема Эйлера. Для любого выпуклого многогранника имеет место соотношение: Y + U — Q = 2, где Y— число граней, U — число вершин, Q — число рёбер многогранника.
Примем её без доказательства. Из нее вытекают следующие следствия. Докажите их самостоятельно, используя теорему Эйлера.
1 следствие. Число плоских углов многогранника в два раза больше числа его рёбер.
2 следствие. Число плоских углов многогранника чётно.
3 следствие. Если в каждой вершине многогранника сходится одно и тоже число рёбер 


4 следствие. Если все грани многогранника являются равными n-угольниками, то справедливо равенство Y = 2Q.
5 следствие. 360° (Y- Q)-сумма всех плоских углов многогранника.
Выпуклый многогранник называют правильным, если его грани
являются равными правильными многоугольниками и в каждой вершине многогранника сходится одно и то же число рёбер. Известно всего пять видов правильных многогранников (проверьте это самостоятельно). Это следующие многогранники:
Исторические сведения:
Все правильные многогранники были известны в Древней Греции. XIII книга знаменитых «Начал» Евклида посвящена правильным многогранникам. Их чаще называют телами Платона. Великий ученых Древней Греции Платон (424-347 гг. до н.э.) в своём идеалистическом изображении мира сравнивает четыре таких тела с 4 элементами вселенной: тетраэдр — пламя, декаэдр — земля, октаэдр — воздух, икосаэдр — вода. А пятый многогранник — додекаэдр называет знаком строения всей вселенной («пятой основой»).
В XVIII веке в теорию многогранников внёс ощутимый вклад Леонард Эйлер (1707-1783) о связи вершин, граней и сторон в выпуклом многоугольнике, изданная в 1758 году и её доказательство упорядочили мир всевозможных многогранников.
Видео:Геометрия 10 кл Понятие многогранникаСкачать

Многогранники в высшей математике
Плоскости в пространстве могут располагаться различным образом.
Плоскости, располагаясь в пространстве различным образом, образуют так называемые пространственные фигуры- многогранники.
Многогранником называется тело, поверхность которого состоит из конечного числа плоских многоугольников, которые называются гранями. У многогранника не менее 4 граней. Отрезки, по которым пересекаются грани, называются рёбрами, а точки в которых пересекаются рёбра, называются вершинами. Отрезок, соединяющий две вершины не лежащие в одной грани, называется диагональю.
Призма — многогранник, две грани которого являются конгруэнтными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами.
Пирамида —это многогранник, одна грань которого многоугольник, а остальные грани — треугольники с общей вершиной.
Призма и пирамида называется по форме многоугольника, лежащего в основании.
Многогранники бывают двух видов: выпуклые и вогнутые. Если многогранник целиком расположен по одну сторону от плоскости каждой его грани, то он является выпуклым. У выпуклого многогранника две произвольным образом взятые точки, соединённые отрезком, располагаются во внутренней области.
Многогранники А и В — выпуклые, С и D — вогнутые.
Выпуклый многогранник, все грани которого являются конгруэнтными правильными многоугольниками, и в каждой его вершине сходится одинаковое число рёбер, называется правильным. Эти фигуры так же называют платоновыми телами. Например, куб является правильным многогранником. Различают пять видов Платоновых тел: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
Призмы
Два конгруэнтных многоугольника, расположенных в параллельных плоскостях и совпадающих при параллельном переносе, и все отрезки, которые соединяют соответствующие точки многоугольников, образуют фигуру, которая называется призмой. Многоугольники называются основаниями призмы, а отрезки прямых, соединяющих соответственные вершины, называются боковыми рёбрами призмы. Часть плоскости, проходящей через боковые рёбра призмы, называется боковыми гранями призмы. Боковые грани призмы параллелограммы. У каждого параллелограмма две стороны соответствуют сторонам основания, а две другие являются боковыми рёбрами. Если боковые рёбра перпендикулярны плоскости основания, то призма называется прямой призмой, если не перпендикулярны, то призма называется наклонной призмой.
Боковые грани правильной призмы прямоугольники. Если в основании прямой призмы лежит правильный многоугольник, то призма называется правильной.
Если в основании призмы лежит 
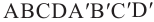
Расстояние между основаниями призмы называется высотой. Боковые рёбра прямой призмы являются её высотами.
Прямая, соединяющая две вершины призмы не принадлежащие одной грани, называется диагональю призмы.
Выберите точку вершины призмы и от неё начертите отрезки: на 2 единицы вниз, на 5 единиц влево и 3 единицы вправо.
Из каждой вершины параллелограмма начертите отрезки длинной 2 еденицы.
Многогранники и их виды с различных сторон
При помощи кубов можно получать различные конструкции. Их называют кубоиды. Виды кубоидов с различных сторон (план) или наоборот, сборка конструкции кубоида по плану имеет большое практическое значение.
Практическая работа. Ниже представлены вид сверху, вид сбоку и вид спереди конструкции фигуры, по которым построена сама фигура и её изображение на изометрической бумаге. Для примера представлено изображение фигуры сверху, сбоку и спереди. Составьте различные конструкции из кубов и изобразите их на изометрической бумаге.
Для изображения трёхмерных фигур удобно использовать изометрическую бумагу. Например, рёбра куба равные единице равны единице расстояния между точками. Получить изображение куба можно отметив вершины и соединив их. Аналогичным образом строятся все кубы из которых состоит кубоид.
Площадь поверхности призмы
Исследование 1. Изобразим развёртку прямоугольного параллелепипеда с измерениями а, b, с.
Поверхность параллелепипеда состоит из 6 попарно конгруэнтных прямоугольников и чтобы вычислить площадь полной поверхности, надо вычислить площади его граней.
Грани Площади 1.Правая и левая:
2.Нижняя и верхняя:
2. Передняя и задняя
Сумма площадей всех граней:
Площадь полной поверхности прямоугольного параллелепипеда с длиной а, шириной b и высотой с вычисляется но формуле 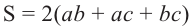
Исследование 2. Площадь боковой и полной поверхности прямой треугольной призмы.
1.Вычислите площадь боковой и полной поверхности прямой треугольной призмы с высотой И сторонами основания а, b , с.
2.Начертим развёртку призмы.
3.Боковая поверхность призмы состоит из трёх прямоугольников. Сумма площадей этих прямоугольников составляет площадь боковой поверхности. Площадь боковой поверхности:
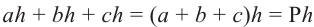
где Р — периметр основания.
4.Чтобы найти площадь полной поверхности, надо найти площади оснований. В нашем случае основание треугольное. Значит, для данной призмы площадь полной поверхности равна сумме площадей двух треугольников и площади боковой поверхности. Здесь площадь треугольника может быть вычислена по формуле Герона.
Исследование 3. Основаниями наклонной призмы являются два прямоугольника со сторонами 10 х 20. Две боковые грани (левая и правая) являются конгруэнтными прямоугольниками с длинами 10 и 18, две оставшиеся грани (передняя и задняя) являются параллелограммами со сторонами 20 и 18 и острым углом 30°. Найдите площадь полной поверхности.
Для того, чтобы найти площади передней и задней поверхностей призмы, являющимися параллелограммами, найдём высоту.
Сумма площадей передней и задней граней: 2 • 20 • 9 = 360 (кв.ед.)
Сумма площадей правой и левой граней: 2 — 10- 18 = 360 (кв.ед.)
Сумма площадей основания: 2 • 20 • 10 = 400 (кв.ед.)
Площадь полной поверхности: 360 + 360 + 400 = 1120 (кв.ед.)
Площадь боковой поверхности прямой призмы
Площадь боковой поверхности прямой призмы равна произведению периметра основания многоугольника на высоту (боковое ребро).
Здесь Р показывает периметр основания, а 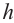
Площадь полной поверхности призмы
Площадь полной поверхности призмы равна сумме площадей основания и боковой поверхности.
Площадь полной поверхности прямой призмы вычисляется по формуле:
Пример №5
Вычислим площадь полной поверхности прямой призмы.
а)Найдём площадь полной поверхности прямой призмы, в основании которой лежит прямоугольный треугольник .
б) Найдём площадь полной поверхности прямой призмы в основании которой лежит трапеция.
Сечение призмы плоскостью
Исследование. Кусок сыра имеет форму прямой призмы. Как нужно разрезать сыр, чтобы полученный ломтик имел форму:
а)прямоугольника
Кусок сыра спереди и сбоку имеет форму прямоугольника. Разрезав сыр по вертикали, получим ломтик прямоугольной формы. б)треугольника
Кусок сыра сверху имеет форму треугольника. Разрезав сыр по горизонтали получим ломтик треугольной формы. в)трапеции
Кусок сыра сбоку имеет вид прямоугольника. Разрезав сыр под определённым углом получим ломтик в форме трапеции.
При сечении призм плоскостью в результате на ней остаётся след, определяющий форму сечения. На рисунке изображены сечения плоскостью прямоугольного параллелепипеда.
Сечение плоскостью параллельной основаниям.
Сечение -прямоугольник.
Сечение плоскостью перпендикулярной основаниям.
Сечение -прямоугольник.
Сечение плоскостью под определённым углом к плоскости основания через противоположные грани.
Сечение -параллелограмм.
Сечение плоскостью под определённым углом к плоскости основания через рёбра из одной вершины.
Сечение -треугольник.
Будьте внимательны! Сечение плоскостью не означает отсечённую часть. Сечение — это след, который остаётся при сечении на плоскости. Плоскость, перпендикулярная боковым рёбрам призмы, называется перпендикулярным сечением. Сечением призмы, параллельное основанию является многоугольник, конгруэнтный основанию.
Сечение, проходящее через боковые рёбра, не принадлежащие одной грани, называется диагональным сечением призмы.
Количество диагональных сечении 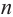
Так как каждое диагональное сечение призмы является параллелограммом, то количество диагоналей 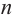
Площадь боковой поверхности призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра: 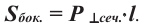
Пример №6
Основанием наклонной призмы является равнобедренный треугольник. Грань АСА’С’ — прямоугольник. Если АА’ = 12 см, АВ = ВС = 8 см, АС = 6 см и а = 30°, найдём площадь боковой поверхности.
Решение: Площадь боковой поверхности призмы: 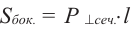
Решение задачи более удобно провести на чертеже представленном в открытом виде. DE и FE равны катетам лежащим напротив угла 30° и следовательно они равны 4 см. Периметр перпендикулярного сечения DEF равен
Пирамида
Одна грань пирамиды многоугольник, все остальные грани — треугольники. Треугольники с общей вершиной являются боковыми гранями, многоугольник — основанием. Общие стороны боковых граней называются рёбрами. Общая вершина для боковых граней, состоящих из треугольников, называется вершиной пирамиды.
Перпендикуляр, опущенный из вершины пирамиды на её основание, называется высотой пирамиды. Правильной называется пирамида, в основании которой лежит правильный многоугольник и основание высоты пирамиды совпадает с центром этого многоугольника.
Высота, проведённая из вершины правильной пирамиды на основание боковой грани (треугольника), называется апофемой.
Пирамида называется по форме многоугольника, лежащего в основании. Например, треугольная пирамида, четырёхугольная пирамида и т.д.
Боковые рёбра правильной пирамиды конгруэнтны. Боковые грани правильной пирамиды конгруэнтные равнобедренные треугольники. Правильная треугольная пирамида ещё называется тетраэдром. Tetra в переводе с греческого четыре, т.е. 4 грани (каждая в форме треугольника).
В частном случае пирамиду можно изобразить следующим образом:
1.Начертите параллелограмм и его диагонали.
2.Из точки пересечения диагоналей восстановите перпендикуляр. 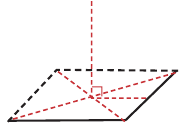
Боковую поверхность правильной пирамиды можно найти как сумму площадей конгруэнтных треугольников.
Например, на рисунке площадь боковой поверхности правильной шестиугольной пирамиды равна сумме площадей 6 конгруэнтных треугольников, из которых состоит боковая поверхность.
Площадь боковой поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра многоугольника, лежащего в основании, и апофемы.
Здесь Р — периметр основания,
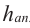
Площадь полной поверхности пирамиды равна сумме площадей основания и боковой поверхности.
Пример №7
Сторона основания правильной шестиугольной пирамиды равна 6 см. Найдём площадь полной поверхности, если апофема равна 9 см.
Решение:
Найдите: 
Чтобы найти площадь основания, сначала надо найти апофему основания 
Центральный угол правильного шестиугольника: 360° : 6 = 60°
Тогда 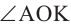
Пример №8
Боковые рёбра правильной треугольной пирамиды равны 10 см, а высота 6 см. Найдём площадь полной поверхности.
Решение:
Дано: АD = 10 см, DO = 6 см
Найдите: 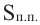
Чтобы найти боковую поверхность пирамиды, надо найти периметр основания и апофему. Для этого достаточно найти одну сторону правильного треугольника.
Из
Известно что 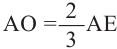
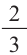
то АЕ = 12 (см). Так как углы 
Найдем апофему из
Сечение пирамиды плоскостью. Усечённая пирамида
Плоскость, параллельная плоскости основания и пересекающая ее боковые ребра, отсекает от нее подобную пирамиду. Другая часть представляет собой многогранник, которой называется усечённой пирамидой. Параллельные грани усечённой пирамиды называются её основаниями, остальные грани — боковой поверхностью. Отрезок перпендикуляра между плоскостями основания называется высотой усечённой пирамиды. Если пирамида правильная, то сечение плоскостью также является правильным многоугольником и усечённая пирамида также является правильной. Боковые грани правильной усечённой пирамиды конгруэнтные трапеции.
Высота этой трапеции являются апофемой правильной усечённой пирамиды.
Площадь боковой поверхности правильной усечённой пирамиды вычисляется по формуле: 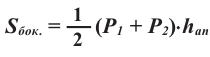
Плоскость, проходящая через два боковых ребра, не принадлежащих одной грани усечённой пирамиды, называется диагональным сечением.
Этапы построения усечённой пирамиды.
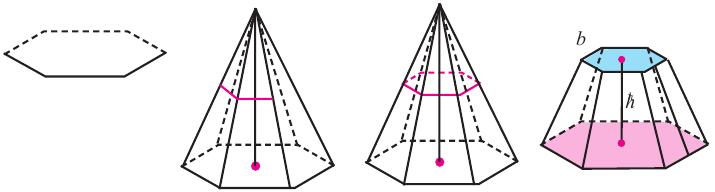
3)На любом ребре пирамиды выберите точку, постройте отрезки, параллельные , сторонам основания, и начертите другое основание. Сотрите боковые рёбра от вершины, до меньшего основания.
Видео:Видеоурок по темам Многоугольники и МногогранникиСкачать

Многогранники и их изображения
В предыдущих классах мы в основном изучали планиметрию — геометрию на плоскости. Теперь, зная свойства плоских геометрических фигур, приступаем к изучению стереометрии (греч. стереос — пространственный) — раздела геометрии, в котором исследуются свойства не только плоских, но и пространственных геометрических фигур, т. е. таких, не все точки которых лежат в одной плоскости: например, параллелепипед и пирамида (рис. 1, а); шар и цилиндр (рис. 1, б).
Представление о пространственных геометрических фигурах дают окружающие нас предметы, если принимать во внимание только их форму и размеры, не интересуясь всеми остальными свойствами: цветом, массой и т. д. Например, апельсин, капля воды в невесомости дают представление о шаре; спичечный коробок и многие жилые дома имеют форму параллелепипеда; усыпальницы египетских фараонов построены в форме пирамиды (рис. 1, в).
Точки и прямые были основными фигурами в планиметрии. Наряду с ними в стереометрии в качестве основных рассматриваются и плоскости. Представление о части плоскости дает поверхность оконного стекла, гладкая поверхность письменного стола или мраморной плитки.
В стереометрии, как и в планиметрии, используются общематематические понятия «принадлежать» или «лежать на», «множество», «число» и т. д.
В пространстве имеется бесконечно много плоскостей, и на каждой из них справедливы аксиомы планиметрии и следствия из них. Поэтому в дальнейшем, рассматривая фигуры, лежащие в какой-либо плоскости, будем пользоваться всеми свойствами этих фигур и теоремами, доказанными в планиметрии. Кроме того, отметим, что признаки равенства и подобия треугольников, изученные в планиметрии, справедливы и для треугольников, лежащих в разных плоскостях.
В стереометрии большую роль играют пространственные представления, развитию которых способствуют различные изображения фигур. Доказательства теорем стереометрии и решения задач сопровождаются изображениями плоских и пространственных фигур на плоскости рисунка (в тетради или на доске). За изображение фигуры принимается фигура, подобная ее проекции на некоторую плоскость, и выбирается такое изображение, которое дает верное представление о форме фигуры, является удобным для изучения ее свойств. При этом некоторые невидимые части фигуры для большей наглядности изображаются штриховой линией (рис. 2, а, б, в).
Перечислим простейшие правила построения изображений фигур.
- За изображение отрезка принимается отрезок. Середина отрезка изображается серединой его изображения; точка, делящая отрезок в отношении
изображается точкой, делящей его изображение в отношении
- Параллельные прямые (отрезки) изображаются параллельными прямыми (отрезками).
- В качестве изображения любого треугольника можно принять произвольный треугольник.
Из правил 2 и 3 следует, что за изображение квадрата, прямоугольника, ромба, параллелограмма можно принять произвольный параллелограмм. В дальнейшем будем этим пользоваться, выполняя изображения фигур.
Многогранники
Ранее уже отмечалось, что одним из объектов изучения стереометрии являются пространственные фигуры, к которым относятся и многогранники. Дадим описание многогранников.
Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости; сами многоугольники называются гранями, их стороны — ребрами многогранника, а их вершины — вершинами многогранника.
Понятие геометрического тела и определение многогранника будут даны позже, а сейчас отметим, что наглядное представление о геометрическом теле дает часть пространства, которую занимает какое-либо физическое тело.
Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней — площадью (полной) поверхности.
Представление о многогранниках дают кристаллы различных минералов, встречающихся в природе. Например, бриллиант представляет собой алмаз, ограненный должным образом, т. е. имеющий форму определенного многогранника. Другими примерами моделей многогранников с достаточной точностью служат книжные полки, шкафы, строящиеся дома и т. д. Как видим, в окружающем нас пространстве есть множество разнообразных предметов, имеющих форму многогранников.
На рисунках 3, а, б, в и 4, а даны изображения некоторых многогранников.
А вот многоугольники, изображенные на рисунке 4, б, в, не ограничивают части пространства, а следовательно, не образуют поверхность одного многогранника.
Многогранник называется выпуклым, если он лежит по одну сторону от плоскости каждой своей грани. Если это условие не выполняется, то многогранник называется невыпуклым. Выпуклые многогранники изображены на рисунках 3, а, б, в. Многогранник, изображенный на рисунке 4, а, невыпуклый.
Дадим описание некоторых выпуклых многогранников.
Куб, параллелепипед
Куб — это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины — вершинами куба. На рисунке 5, a, б даны изображения куба. Изображение на рисунке 5, а является более наглядным.
Заметим, что шесть равных квадратов в пространстве могут быть расположены так, что они не будут гранями одного куба, например, как показано на рисунке 5, в.
Параллелепипед — это многогранник, у которого шесть граней и каждая из них — параллелограмм.
Стороны параллелограммов называются ребрами параллелепипеда, а их вершины — вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными.
Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани — боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, — его боковыми ребрами.
Прямой параллелепипед — это такой параллелепипед, у которого боковые грани — прямоугольники.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники. Представление о форме прямоугольного параллелепипеда дают спичечный коробок, строительный кирпич или каждая из моделей, которые получаются при распиливании на две части модели куба, сделанной из дерева, как показано на рисунке 6, а.
Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный. Основанием прямого параллелепипеда может служить параллелограмм, не являющийся прямоугольником. Представление о прямом, но не прямоугольном параллелепипеде дает, например, комната, в которой пол и потолок имеют форму ромба, не являющегося квадратом.
Изображения параллелепипеда даны на рисунке 6, б, в.
Если основаниями параллелепипеда служат параллелограммы 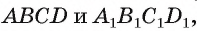
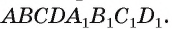
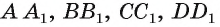
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. На рисунке 7, а отмечены противолежащие вершины О к F параллелепипеда.
Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали. На рисунках 7, б изображены две диагонали параллелепипеда.
Призма и пирамида
Призма (n-угольная) — это многогранник, у которого две грани — равные n-угольники, а остальные n граней — параллелограммы. Равные n-угольники называются основаниями, а параллелограммы — боковыми гранями, призмы.
Прямая призма — это такая призма, у которой боковые грани — прямоугольники.
Представление о форме прямой призмы дают, например, модели, которые получаются в результате распиливания деревянного бруска, имеющего форму прямоугольного параллелепипеда, вдоль ребра, как показано на рисунке 8, а. При этом получаются две модели, одна из которых представляет собой модель прямой пятиугольной призмы, а другая — модель прямой треугольной призмы.
Правильная n-угольная призма — это призма, у которой все боковые грани — прямоугольники, а ее основания — правильные га-угольники.
Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается 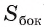
Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается 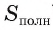
Если основания призмы есть «-угольники 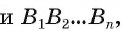
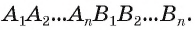
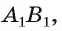
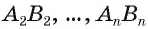
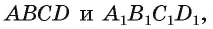
Пирамида (n-угольная) — это многогранник, у которого одна грань — какой-нибудь n-угольник, а остальные n граней — треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.
Пирамида, вершина которой — точка S, а основание — n-угольник 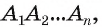
Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается 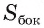
Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается 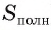
Правильная n-угольная пирамида — это такая пирамида, основание которой — правильный n-угольник, а все боковые ребра равны между собой.
У правильной пирамиды боковые грани — равные друг другу равнобедренные треугольники.
Треугольная пирамида называется тетраэдром, если все ее грани — равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды.
Заметим, что не всякая правильная треугольная пирамида является тетраэдром.
На рисунке 9, а дано изображение правильной четырехугольной пирамиды SABCD. Пространственные фигуры, изображенные на рисунке 9, б, в, не являются пирамидами, так как указанные треугольники и четырехугольник не ограничивают части пространства.
В дальнейшем, если дано изображение какого-либо многогранника, иногда будем говорить, что дан многогранник.
Аксиомы стереометрии
В первом параграфе уже отмечалось, что в стереометрии основными фигурами являются точки, прямые и плоскости. Как и в планиметрии, точки обозначаются заглавными латинскими буквами А, В, С. а прямые — строчными латинскими буквами а, в, с. или двумя заглавными латинскими буквами АВ, СЕ и т. д., плоскости — строчными буквами греческого алфавита 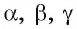
Если точка А лежит на прямой а (в плоскости 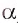
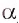
Если точка В не принадлежит прямой а (плоскости 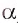
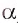
Например, на рисунке 18, а, б изображены точки А и О, лежащие на прямой 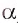
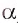
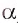
Свойства геометрических фигур в пространстве устанавливаются путем логических рассуждений на основе некоторых утверждений (аксиом), которые принимаются без доказательств.
Часть аксиом, используемых в стереометрии, известны уже из курса планиметрии. Здесь сформулируем только три аксиомы о взаимном расположении точек, прямых и плоскостей, которые являются специфически пространственными.
А 1. Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
Плоскость, проходящую через точки А, В и С, не лежащие на одной прямой, обозначают ABC или (ABC).
Например, на рисунке 19, а, б изображена треугольная пирамида DABC. Плоскость 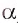
На аксиоме А 1 основано устройство штативов некоторых измерительных приборов. Острия ножек штатива расположены в одной плоскости, поэтому измерительный прибор занимает устойчивое положение.
А 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Если каждая точка прямой а лежит в плоскости 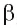
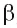
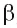
На рисунке 20, а, б 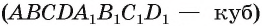
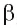
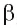
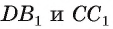
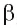
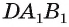
Если прямая а и плоскость а имеют только одну общую точку О, то говорят, что они пересекаются в точке О, и пишут:
На рисунке 20, а, б изображена прямая 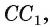
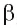
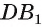
А 3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Если прямая а — общая прямая плоскости 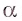
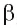
Например, на рисунке 21, 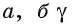
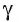
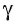
Пример №9
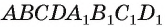
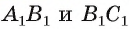
1)Так как 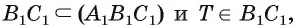
2)Поскольку
3) Таким образом, 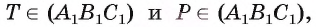
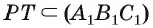
Пример №10
Плоскости 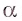
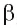
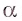
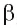
Пусть прямая b и плоскость 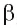
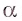
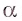
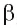
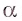
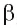
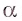
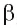
Пример №11
Дан куб 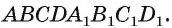
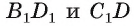
Решение:
1)Точка Т есть точка пересечения диагоналей грани 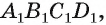
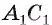
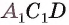
2)В треугольнике 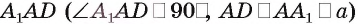
3)Отрезок TO — средняя линия треугольника
Следовательно,
Ответ:
Пример №12
Найдите расстояние от вершины В куба 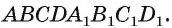
Решение:
1)Треугольник 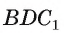
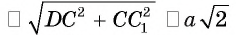
2)Точка О — середина отрезка 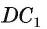
3)Так как треугольник 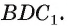
Следствия из аксиом
Из курса планиметрии мы уже знаем, что утверждение, справедливость которого обосновывается путем логических рассуждений, называется теоремой, а само обоснование — доказательством. Докажем некоторые следствия из аксиом. Доказать теорему — значит путем рассуждений обосновать, что она следует из некоторых аксиом или ранее доказанных теорем. Очевидность не является критерием справедливости теорем, поэтому в процессе доказательств, обращаясь к рисункам, необходимо одновременно следить за правильностью рассуждений, чтобы быть уверенными в справедливости сделанных выводов.
Теорема 1. Через прямую и не лежащую на ней точку проходит единственная плоскость.
I.Докажем, что такая плоскость существует.
1)Пусть точка А не лежит на прямой
2)Отметим на прямой b две точки Т и С.
3)Точки А, Т и С не лежат на одной прямой, следовательно, по аксиоме А 1 через эти точки проходит некоторая плоскость 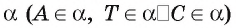
4)Точки Т и С прямой b лежат в плоскости а, значит, по аксиоме А 2 плоскость а проходит через точку А и прямую 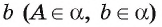
II.Докажем единственность этой плоскости.
1) Допустим, что существует еще одна плоскость 
2) Так как плоскость 
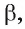
3) По аксиоме А 1 существует только одна плоскость, проходящая через точки А, Т и С, не лежащие на одной прямой. Следовательно, плоскость 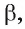
Например, пусть 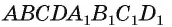
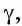
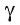
Через прямую AD и точку Б, проходит единственная плоскость 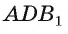
Теорема 2. Через две пересекающиеся прямые проходит единственная плоскость.
I. Докажем, существование плоскости.
1)Пусть прямые а и b пересекаются в точке 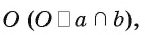
2)Тогда по теореме 1 существует плоскость а, проходящая через точку Е и прямую
3) Точки О и Е прямой b лежат в плоскости а, следовательно, по аксиоме А 2 плоскость а проходит через прямую b. Таким образом, существует плоскость а, проходящая через прямые а и b.
II. Докажем, что такая плоскость единственная.
1)Допустим, что существует еще одна плоскость 
2)Точка Е лежит на прямой b, следовательно, плоскость 
Например, пусть 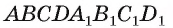
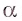
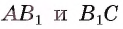
Плоскости 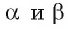
В заключение подчеркнем, что в силу теорем 1 и 2 возможны еще два способа задания плоскости: а) существует единственная плоскость, проходящая через прямую и не принадлежащую ей точку; б) существует единственная плоскость, проходящая через две пересекающиеся прямые.
Построение сечений многогранников плоскостью
Для решения задач по стереометрии часто необходимо умение строить на рисунке сечения многогранников (например, пирамиды, параллелепипеда, куба, призмы) некоторой плоскостью. Поясним, что понимается под сечением.
Секущей плоскостью пирамиды (призмы, параллелепипеда, куба) называется такая плоскость, по обе стороны от которой есть точки данной пирамиды (призмы, параллелепипеда, куба).
Сечением пирамиды (призмы, параллелепипеда, куба) называется фигура, состоящая из всех точек, которые являются общими для пирамиды (призмы, параллелепипеда, куба) и секущей плоскости. 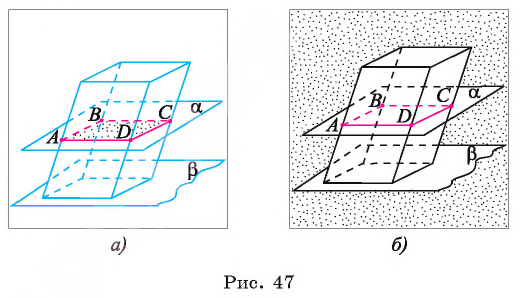
Секущая плоскость пересекает грани пирамиды (параллелепипеда, призмы, куба) по отрезкам, поэтому сечение есть многоугольник, лежащий в секущей плоскости, сторонами которого являются указанные отрезки.
Например, на рисунке 47, а, б изображен параллелепипед и секущая плоскость 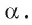
Для построения сечения пирамиды (призмы, параллелепипеда, куба), а точнее, его изображения можно построить точки пересечения секущей плоскости с ребрами пирамиды (призмы, параллелепипеда, куба) и соединить каждые две из них, лежащие в одной грани.
Заметим, что последовательность построения вершин и сторон сечения не существенна, но выполнять построение необходимо с учетом аксиом и теорем стереометрии, а также правил изображения фигур. Подчеркнем, что в основе построения сечений многогранников лежит две задачи на построение: а) линии пересечения двух плоскостей; б) точки пересечения прямой и плоскости.
а) Для построения прямой, по которой пересекаются некоторые две плоскости 
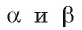
б) Для построения точки пересечения прямой 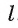
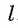
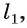
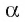
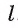
Пример №13
На ребрах AD, DC и СВ треугольной пирамиды DABC даны точки Т, О и Е соответственно. Точка О не является серединой ребра DC (рис. 48, а, б, в). Постройте сечение пирамиды плоскостью TOE.
Решение:
1) Проводим отрезки ТО и ОЕ (см. рис. 48, а). (Отрезки ТО и ОЕ лежат в секущей плоскости и в гранях ACD и CBD соответственно, поэтому являются сторонами искомого сечения.)
2)Находим точку 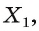
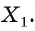
3)Отметим точку 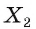
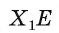

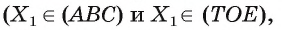
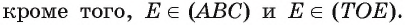
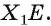
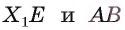
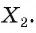
4)Проводим отрезок 
Четырехугольник 
Пример №14
Точка Т — середина ребра DB тетраэдра DABC (рис. 49, а, б). Постройте сечение тетраэдра плоскостью, проходящей через точки А, С и Т. Вычислите радиус окружности, вписанной в это сечение, если длина ребра данного тетраэдра равна 2 см.
Решение:
I. Построим сечение.
Точки Т и С лежат в каждой из плоскостей АТС и DBC, следовательно, плоскость АТС пересекает плоскость DBC по прямой ТС, а, значит, грань DBC — по отрезку ТС. Аналогично получаем, что секущая плоскость АТС пересекает грань ADB по отрезку AT, а каждую из граней ADC и ABC — по отрезку АС. Таким образом, треугольник АТС — искомое сечение данного тетраэдра DABC (см. рис. 49, а, б).
II. Вычислим, радиус окружности.
1) Так как треугольники AT В и СТВ равны

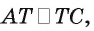
2) В прямоугольном треугольнике СТВ ( 

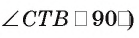
3) Пусть точка Е — середина отрезка АС, точка О — центр окружности, вписанной в треугольник АТС, а точка К — точка касания окружности и стороны ТС. В прямоугольном треугольнике 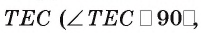
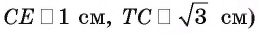
4) Имеем 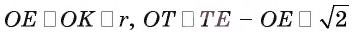

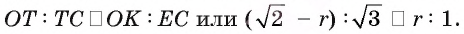
Заметим, что радиус r можно найти, воспользовавшись
формулой 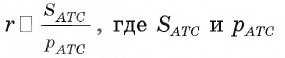
Подробное построение сечений многогранников
А) При изучении стереометрии приходится пространственные фигуры показывать на плоских рисунках. Часто на рисунке нужно показать взаимное расположение двух фигур. Если одна из фигур — многогранник, а вторая — плоскость, то их взаимное расположение характеризует та часть многогранника, которая принадлежит рассматриваемой плоскости, или, иными словами, сечение многогранника плоскостью. Плоскость при этом называют секущей плоскостью.
Секущая плоскость пересекает поверхность многогранника по отрезкам, а сечением многогранника плоскостью является один или несколько многоугольников.
На рисунке 106 изображено сечение пятиугольной призмы, которое является семиугольником. Сечение «рамы» плоскостью на рисунке 107 состоит из двух четырёхугольников.
Для построения сечения многогранника достаточно построить общие точки его граней и секущей плоскости.
Пример №15
Построим сечение треугольной пирамиды 
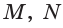
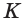
Секущая плоскость 
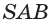
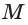
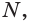
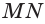
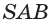
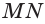
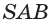
Рассуждая аналогично, получаем, что плоскость 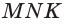
Треугольник 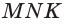
Пример №16
Построим сечение треугольной пирамиды 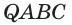
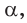
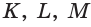
Секущая плоскость 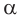
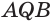
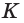
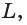
Поскольку точки 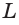
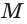
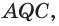
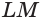
Грань 
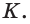
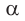
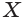
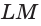
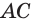
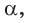
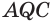
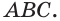
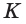
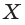
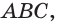
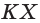
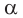
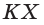
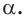
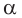
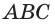
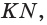
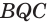
Четырёхугольник 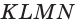
Прямые 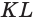
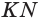
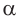
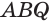
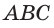
Пример №17
Построим сечение пирамиды 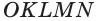
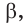
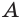
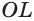
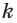
Найдём точку 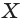
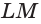
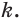
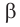
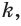
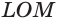
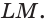
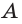
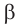
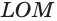
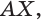
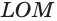
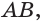
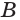
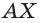
Аналогично найдём точки 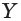
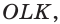
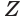
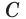
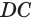
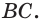
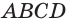
Б) 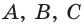
Построение искомого сечения зависит от того, на каких рёбрах призмы лежат точки 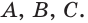
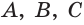
Пример №18
Точки 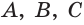
Вначале построим след секущей плоскости 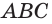
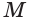
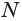
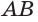
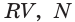
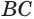
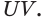
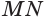
Точка 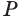
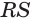
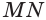
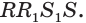
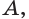
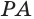
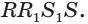
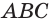
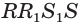
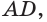
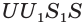
Искомым сечением является четырёхугольник
Видим, что новым элементом в этом решении в сравнении с примером 2 является построение следа секущей плоскости на плоскости основания.
Пример №19
Точки 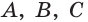
Вначале построим след секущей плоскости 
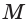
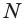
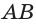
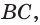
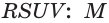
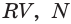
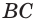
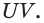
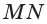
Точка 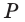
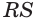
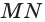
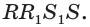
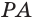
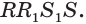
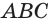
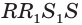
Найдём точку 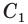
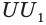
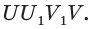
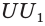
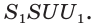
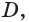
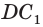
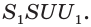
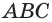
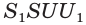
Искомым сечением является пятиугольник ABCED.
Пример №20
Точки 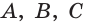
След 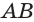
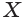
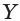
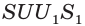
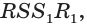
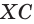
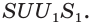
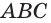
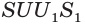
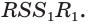
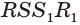
Пример №21
Постройте сечение куба 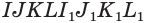
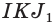
Решение:
Плоскость 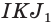
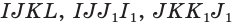
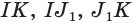
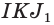
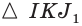
или
Следовательно, 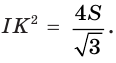
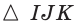
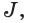
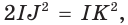
Ответ:
Пример №22
Постройте сечение правильной пирамиды 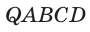
Решение:
Пусть 
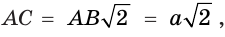
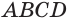
В 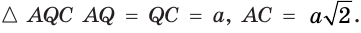
Ответ:
«Знание только тогда является знанием, когда оно приобретено усилиями своей мысли, а не памятью» (Л. Н. Толстой).
Многограники в геометрии
Геометрия — это настоящая естественная наука, только более простая, а значит, и более совершенная, чем любая другая.
Огюст Конт, французский философ
Среди твердых тел естественного и искусственного происхождения особенно важную роль играют многогранники. Подобно многоугольникам на плоскости, они наглядно демонстрируют, как объединение известных свойств простейших геометрических фигур рождает новые, до сих пор неизвестные факты. Недаром, говоря о всесторонне одаренном человеке, мы часто отмечаем многогранность его таланта.
Для успешного изучения многогранников необходимо восстановить в памяти свойства многоугольников, а также основные теоремы о расположении прямых и плоскостей в пространстве. Именно на этом теоретическом материале базируются основные теоремы данной главы.
Свойства многогранников находят широкое практическое применение в искусстве и строительстве, кристаллографии и компьютерной графике. Выдающийся архитектор XX столетия Ле Корбюзье справедливо отмечал, что шедевры старинной архитектуры появились только благодаря законам геометрии. И значительную часть этих бесценных для практической деятельности человека законов таят в себе именно многогранники.
Двугранные и многогранные углы. многогранник
Понятие двугранного угла рассматривалось нами в курсе геометрии 10 класса. Вспомним, как вводилось это понятие.
Двугранный угол
В планиметрии углом называется фигура, состоящая из двух лучей с общим началом. По аналогии в пространстве можно рассматривать две полуплоскости с общей граничной прямой. Если мы перегнем по прямой лист бумаги, то получим модель такой пространственной фигуры.
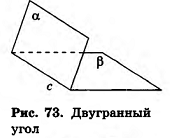
Определение:
Двугранным углом называется фигура, состоящая из двух полуплоскостей (граней двугранного угла) с общей граничной прямой (ребром двугранного угла).
На рисунке 73 изображен двугранный угол с гранями 
Измерение двугранных углов сводится к измерению углов между лучами, выполнить которое можно с помощью дополнительных построений следующим образом.
Через точку О на ребре данного двугранного угла (рис. 75) проведем плоскость, перпендикулярную ребру угла. Она пересекает грани угла по лучам OA и ОВ, перпендикулярным ребру данного угла. Угол АОВ, образованный этими лучами, называют линейным углом данного двугранного угла. Часто при построении линейного угла двугранного угла плоскость, перпендикулярную ребру, не строят, ограничиваясь проведением
в гранях данного угла лучей с общим началом, перпендикулярных ребру угла.
Очевидно, что двугранный угол имеет множество линейных углов. Покажем, что все линейные углы двугранного угла равны.
Действительно, пусть 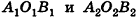
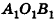
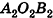
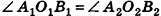
Определение:
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Из доказанного следует, что градусная мера двугранного угла не зависит от выбора линейного угла.
Согласно определению угла в планиметрии, градусная мера двугранного угла лежит в пределах от 0° до 180° (случаи, когда грани двугранного угла совпадают или принадлежат одной плоскости, как правило, не рассматриваются). Как и среди углов на плоскости, среди двугранных углов различают острые (меньше 90°), прямые (те, что равны 90°) и тупые (больше 90° и меньше 180°).
Итак, для обоснования градусной меры двугранного угла необходимо построить его линейный угол, то есть указать на гранях данного двугранного угла два луча с общим началом, перпендикулярных ребру угла.
Один из способов построения таких лучей описан в решении следующей задачи.
Пример:
На одной из граней двугранного угла, равного 45°, лежит точка, удаленная на 8 см от ребра угла. Найдите расстояние от этой точки до другой грани угла.
Решение:
Пусть точка А принадлежит грани а данного двугранного угла (рис. 77). Проведем 
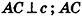
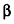
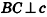
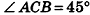
Ответ: 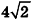
Говорят, что точка М лежит внутри двугранного угла, если существует линейный угол данного двугранного угла, во внутренней области которого лежит точка М. Так, на рисунке 77 во внутренней области данного двугранного угла лежит любая внутренняя точка отрезка АВ. Множество всех точек, лежащих внутри двугранного угла, называется внутренней областью двугранного угла.
Трехгранный и многогранный углы
Рассмотрим лучи 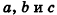
Определение:
Трехгранным углом называется фигура, состоящая из трех плоских углов с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости.
На рисунке 78 трехгранный угол с вершиной Р образован плоскими углами (ab), (bс) и (ас). Эти плоские углы называются гранями трехгранного угла, а их стороны 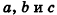
Пример: (неравенство треугольника для трехгранного угла)
Любой плоский угол трехгранного угла меньше суммы двух других плоских углов. Докажите.
Решение:
Пусть РА, РВ и PC — ребра трехгранного угла с вершиной Р, а угол АРС — наибольший из плоских углов данного угла (рис. 79). В грани АРС проведем луч РК так, чтобы 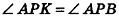
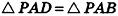
Пусть лучи AD и PC пересекаются в точке Е. Тогда из треугольника ABE по неравенству треугольника АЕ 2 , 8 м 2 и 32 м 2 . Найдите диагональ параллелепипеда.
Решение:
Пусть 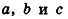
Перемножив правые и левые части уравнений системы, получим 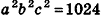
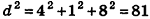
Определение:
Кубом называется прямоугольный параллелепипед, у которого все ребра равны.
На рисунке 94 изображен куб 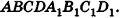
Связь между изученными видами призм иллюстрирует схема на с. 100.
Правила определения понятий
Формулирование верных с точки зрения логики определений основных понятий всегда является одной из наиболее сложных проблем любой науки. Не является исключением и геометрия: оказывается, что такие общеизвестные и легкие для распознавания фигуры, как призма, пирамида и т. п., таят логические ловушки, в которые попадали даже известные ученые, пытаясь дать строгие определения этих фигур.
Особенно много логических ошибок связано с определением призмы. Например, в одном из учебников геометрии было приведено такое определение: «Призмой называется многогранник, две грани которого — равные многоугольники с соответственно параллельными сторонами, а остальные грани — параллелограммы». Казалось бы, все верно — любая призма действительно удовлетворяет такому определению. Но посмотрим на рисунок 95: фигура, изображенная на нем, представляет собой объединение двух треугольных призм — прямой (она находится внизу) и наклонной, в основаниях которых лежат равные треугольники. Конечно же, такая фигура не является призмой, но она полностью удовлетворяет приведенному выше определению (убедитесь в этом самостоятельно).
В чем же кроется причина ошибки? В любом определении мы имеем дело с двумя понятиями — определяемым (в данном случае это понятие «призма») и тем, с помощью которого мы описываем определяемое понятие (в данном случае это понятие многогранник, две грани которого — равные многоугольники с соответственно параллельными сторонами, а остальные грани — параллелограммы»). Одно из основных требований к логически верным определениям заключается в том, чтобы оба эти понятия были тождественными, то есть описывали одно и то же множество предметов. А в нашем случае множество многогранников, грани которых имеют описанные свойства, шире множества призм, то есть кроме собственно призм включает в себя и другие многогранники (в частности, фигуру на рис. 95).
Чтобы помочь вам избежать подобных ошибок, определим три основных правила формулирования определения понятий.
1)Определение должно быть соразмерным, то есть множество предметов, которые представляют определяемое понятие, должно совпадать с множеством предметов, с помощью которых мы его описываем. Если этого правила не придерживаться, возникают типичные ошибки:
•слишком широкое определение (описание включает кроме предметов, являющихся представителями определяемого понятия, и другие предметы): например, определение «Лампа — это источник света» является неверным, так как кроме ламп существуют и другие источники света;
•слишком узкое определение (определяемое понятие в полной мере не соответствует приведенному описанию): например, определение «Дробь называется неправильной, если ее числитель больше знаменателя» не учитывает неправильную дробь, равную единице;
•определение в одном смысле широкое, а в другом — узкое: например, определение «Бочка — это емкость для хранения жидкостей», с одной стороны, широкое (емкостями для хранения жидкостей являются также ведра, бутылки и др.), а с другой — узкое (в бочке можно хранить не только жидкости).
2)Определение не должно содержать «логического круга», то есть определяемое понятие и понятие, с помощью которого его определяют, нельзя описывать друг через друга. Например, если мы определяем вращение как движение вокруг оси, то не можем определять ось как прямую, вокруг которой осуществляется вращение. «Логический круг» возникает и тогда, когда оба понятия в определении выражены практически одними и теми же словами. Например: «Фильтр — это прибор, с помощью которого осуществляется фильтрация» или «Гомотетией называется преобразование, которое переводит данную фигуру в гомотетичную» (такие логические ошибки называют тавтологиями).
3)Определение должно быть четким и понятным, то есть оно не должно содержать не свойственных науке двузначностей, метафор, сравнений, как, например, «Повторение — мать учения», «Математика — царица наук» и т. д.
Придерживаясь этих правил, вы сможете четко выражать свои мысли и объяснять собеседнику, что именно вы имеете в виду,— а это умение является залогом успеха не только в геометрии, но и в любой области вашей будущей деятельности.
Пирамида
Пирамида — греческое слово. По одной версии, происходит от египетского «пер о» — большой дом (так египтяне называли усыпальницы фараонов), по другой — от греческого «пор» — огонь (пирамиды традиционно связывали со стихией огня).
Пирамида и ее элементы
Рассмотрим изображенный на рисунке 98 многоугольник 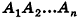
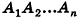
Определение:
Пирамидой называется многогранник, который состоит из плоского многоугольника (основания пирамиды), точки, не лежащей в плоскости основания (вершины пирамиды), и всех отрезков, соединяющих вершину с точками основания.
На рисунке 98 изображена пирамида с вершиной Р, основание которой — плоский n-угольник 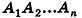
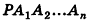
Отрезки 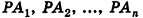
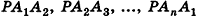
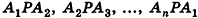
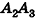
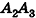
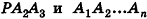
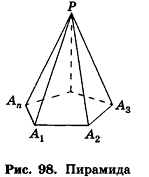
Треугольную пирамиду иначе называют тетраэдром (рис. 99). Так как все грани тетраэдра — треугольники, любую его грань можно считать основанием (для произвольной пирамиды это не так).
В школьном курсе мы будем рассматривать только те пирамиды, основания которых — выпуклые многоугольники. Такие пирамиды являются выпуклыми многогранниками.
Определение:
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания.
На рисунке 99 отрезок РО — высота треугольной пирамиды РАВС.
Изображение пирамиды строят по правилам параллельного проектирования. Построение обычно начинают с основания. Затем обозначают вершину пирамиды и соединяют ее с вершинами основания. Для некоторых видов пирамид, которые будут рассматриваться дальше, целесообразно после построения основания пирамиды сразу же построить ее высоту.
Площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней, а площадью полной поверхности — сумма площадей основания и боковой поверхности:
Правильная пирамида
Определение:
Правильной пирамидой называется пирамида, основанием которой является правильный многоугольник, а основание высоты пирамиды совпадает с центром этого многоугольника.
На рисунке 100 изображена правильная четырехугольная пирамида PABCD. Ее основанием служит квадрат ABCD, а основание высоты РО — точка О — является точкой пересечения диагоналей (центром) этого квадрата. Обоснуем на примере данной пирамиды некоторые свойства правильных пирамид (для произвольной пирамиды доказательство аналогично). Сначала докажем, что прямоугольные треугольники РАО, РВО, РСО и PDO равны. Действительно, так как точка О — центр окружности, описанной около основания пирамиды, то OA = OB = OC = OD . Тогда 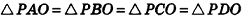
Определение:
Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины.
На рисунке 100 отрезок РМ — апофема правильной пирамиды PABCD. Так как все боковые грани правильной пирамиды равны, то и все апофемы правильной пирамиды равны. А из этого, в частности, следует, что все двугранные углы при основании правильной пирамиды равны (обоснуйте это самостоятельно).
Теорема (формула площади боковой поверхности правильной пирамиды)
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра ее основания на апофему:
Пусть сторона основания правильной n-угольной пирамиды равна а, а апофема — I. Тогда площадь одной боковой грани пирамиды равна —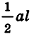
Пример:
В правильной треугольной пирамиде двугранный угол при основании равен а. Найдите площадь боковой поверхности пирамиды, если ее высота равна Н.
Решение:
1. Пусть дана правильная треугольная пирамида РАВС (рис. 101), 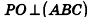
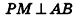
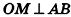
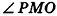
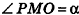
Найдем площадь боковой поверхности пирамиды.
2.
3. Из треугольника РМО
4. Отрезок ОМ — радиус окружности, вписанной в треугольник ABC. Тогда ОМ = 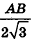
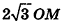
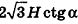
5.
Ответ:
Заметим, что при решении многих задач, связанных с правильными пирамидами, отдельно рассматривают прямоугольные треугольники РАО и РМО (рис. 101) В частности, в треугольнике РАО РО — высота пирамиды, РА — боковое ребро, АО — радиус окружности, описанной около основания пирамиды; в треугольнике РМО РО — высота пирамиды, РМ — апофема, МО — радиус окружности, вписанной в основание пирамиды.
Нахождение расстояния от точки до плоскости боковой грани пирамиды
В некоторых задачах, связанных с пирамидами, необходимо найти расстояние от данной точки пирамиды до боковой грани, не содержащей данную точку. Пусть, например, в правильной треугольной пирамиде РАВС (рис. 102) нужно построить расстояние от основания высоты РО — точки О — до боковой грани РВС. Ясно, что можно было бы опустить из точки О перпендикуляр ON к плоскости РВС. Но такое построение не позволяет сразу определить особенности расположения точки N в треугольнике РВС, которые могут быть использованы в процессе дальнейшего решения задачи. Между тем, оказывается, что точка N принадлежит апофеме РМ данной пирамиды.
Для того чтобы получить этот факт в процессе нахождения расстояния от точки О до плоскости РВС, можно рассуждать следующим образом.
- Пусть
, РМ — апофема данной правильной пирамиды. Так как
, а отрезок ОМ — проекция наклонной РМ на плоскость ABC, то по теореме о трех перпендикулярах
.
- Так как прямая ВС перпендикулярна двум прямым плоскости POM
, то по признаку перпендикулярности прямой и плоскости
.
- Так как плоскость РВС содержит прямую ВС, перпендикулярную плоскости РОМ, то по признаку перпендикулярности плоскостей
.
- Проведем в плоскости РОМ перпендикуляр ON к прямой РМ. Тогда
по свойству двух перпендикулярных плоскостей. Значит, отрезок ON — расстояние от точки О до плоскости РВС.
Таким образом, мы построили отрезок ON не как перпендикуляр к плоскости боковой грани пирамиды, а как перпендикуляр к апофеме, и доказали, что он в то же время является перпендикуляром к плоскости РВС.
Пример:
Высота правильной четырехугольной пирамиды образует с плоскостью боковой грани угол 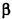
Решение:
1. Пусть дана правильная четырехугольная пирамида PABCD (рис. 103, a), 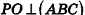
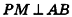
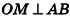
2. Так как 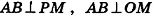
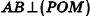
3. Так как плоскость РАВ содержит прямую АВ, перпендикулярную плоскости РОМ, то по признаку перпендикулярности плоскостей 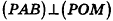
4. Проведем в плоскости РОМ из точки О и из точки L — середины высоты РО — перпендикуляры: 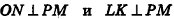
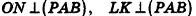
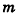

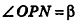
Найдем площадь полной поверхности пирамиды.
5. 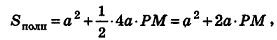
6. Из треугольника PKL 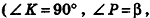
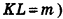
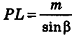
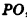
7. Из треугольника POM
8. Так как точка О — центр квадрата ABCD, 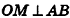
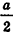
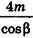
9.
Ответ:
Некоторые виды пирамид
Решение стереометрических задач, связанных с пирамидами, обычно начинается с построения рисунка. Но во многих случаях для правильного отображения на рисунке взаимного расположения элементов пирамиды (в частности, положения ее высоты) необходимо провести предварительный анализ условия задачи и на основании существующих данных определить свойства пирамиды. Попробуем установить такие свойства для отдельных видов пирамид.
Пирамиды, в которых высота принадлежит плоскостям одной или двух боковых граней
Рассмотрим сначала пирамиду, в которой две боковые грани перпендикулярны плоскости основания. По теореме о двух плоскостях, перпендикулярных третьей, прямая пересечения плоскостей, содержащих данные боковые грани, перпендикулярна плоскости основания. Следовательно, если две боковые грани пирамиды перпендикулярны плоскости основания, то прямая их пересечения содержит высоту пирамиды. Например, на рисунке 106, а соседние грани РАВ и РАС пирамиды РАВС перпендикулярны плоскости основания ABC, а высотой пирамиды является их общее ребро РА. На рисунке 106, б изображен более сложный случай: грани РАВ и PCD, которые не являются соседними, перпендикулярны плоскости основания пирамиды, а высота пирамиды РО лежит на прямой пересечения плоскостей РАВ и PCD вне данной пирамиды (объясните, почему эти плоскости пересекаются).
Рассмотрим теперь пирамиду РАВС, в которой одна боковая грань РАС перпендикулярна плоскости основания ABC (рис. 107). Нетрудно догадаться, что высота данной пирамиды РО будет принадлежать плоскости грани РАС. Но если провести из вершины пирамиды перпендикуляр РО к плоскости ABC, то обоснование принадлежности точки О прямой АС будет достаточно громоздким. В этом случае стоит прибегнуть к «хитрости» — воспользоваться тем, что перпендикуляр, проведенный в одной из двух перпендикулярных плоскостей к прямой пересечения этих плоскостей, является перпендикуляром к другой плоскости. Итак, проведем в плоскости РАС перпендикуляр РО к прямой АС; тогда по упомянутому свойству перпендикулярных плоскостей 
Таким образом, если в пирамиде одна боковая грань перпендикулярна плоскости основания, то высота пирамиды принадлежит плоскости этой грани и является перпендикуляром, проведенным из вершины пирамиды к прямой пересечения плоскости данной грани с плоскостью основания. Заметим, что основание высоты РО может лежать как на отрезке АС (рис. 107, а), так и вне его (рис. 107, б).
Пример:
Основанием пирамиды является правильный треугольник. Одна боковая грань пирамиды перпендикулярна основанию, а две другие наклонены к нему под углом 
Решение:
1.Пусть дана треугольная пирамида РАВС, в основании ‘которой лежит правильный треугольник ABC, 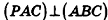
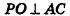
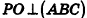
2.Проведем из точки О перпендикуляры к сторонам основания: 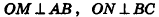
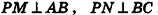
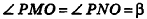
Найдем площадь боковой поверхности пирамиды.
3.
4.Прямоугольные треугольники 
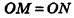
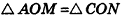
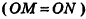
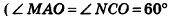
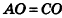
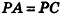
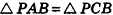
5.Из треугольника
6.Из треугольника
Так как О — середина АС, то
7.
Ответ:
Заметим, что геометрическая конфигурация данной задачи позволяет получить еще один полезный факт: если две соседние боковые грани пирамиды наклонены к ее основанию под равными углами, то основание высоты пирамиды лежит на биссектрисе угла между ребрами основания, принадлежащими данным боковым граням. Обоснуйте этот факт самостоятельно.
Другой способ вычислений, который можно использовать для решения этой задачи, будет описан в п. 9.3.
Пирамиды, в которых основанием высоты является центр окружности, описанной около основания пирамиды
В пункте 9.1 мы рассмотрели случаи, когда предварительный анализ условия задачи существенно влияет на построение рисунка и ход решения. Рассмотрим еще один подобный пример.
Пример:
Основанием пирамиды является прямоугольный треугольник с катетами 6 см и 8 см. Все боковые ребра пирамиды равны 13 см. Найдите высоту пирамиды.
Решение:
Решение этой задачи можно начать с построения изображения данной пирамиды РАВС с основанием ABC ( 
Так как точка Р равноудалена от вершин треугольника ABC, то основание перпендикуляра, проведенного из данной точки к плоскости ABC, является центром окружности, описанной около основания пирамиды. Значит, точка О — центр окружности, описанной около треугольника ABC. Так как в прямоугольном треугольнике центр описанной окружности является серединой гипотенузы, то точка О — середина отрезка АС. Таким образом, условию данной задачи соответствует рисунок 109, б. Завершим теперь решение задачи.
Из треугольника ABC по теореме Пифагора АС = 10 см, значит, АО = ОС = 5 см.
Из треугольника РОА 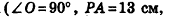
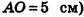
Только что приведенные рассуждения можно обобщить для произвольной пирамиды.
Пример: (о пирамиде с равными боковыми ребрами)
Если все боковые ребра пирамиды равны, то основанием ее высоты является центр окружности, описанной около основания пирамиды. Докажите.
Решение:
Для данной пирамиды 
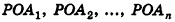
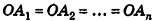
Опираясь на другие признаки равенства прямоугольных треугольников, нетрудно получить еще одно полезное обобщение.
Если в пирамиде выполняется хотя бы одно из условий:
- все боковые ребра равны;
- все боковые ребра образуют равные углы с плоскостью основания пирамиды;
- все боковые ребра образуют равные углы с высотой пирамиды, то основанием высоты пирамиды является центр окружности, описанной около основания пирамиды.
Наличие хотя бы одного из этих условий указывает на то, что около основания данной пирамиды можно описать окружность, центр которой является основанием ее высоты. Более того, имеет место обратное утверждение. Сформулируйте и докажите его самостоятельно.
Заметим также, что при решении многих задач, связанных с пирамидами, имеющими описанные выше свойства, отдельно рассматривают прямоугольный треугольник 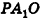
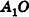
Пирамиды, в которых основанием высоты является центр окружности, вписанной в основание пирамиды
Рассмотрим еще одну задачу, важным этапом решения которой является определение положения основания высоты пирамиды.
Пример:
Основанием пирамиды является ромб с диагоналями 10 см и 24 см. Все двугранные углы при основании пирамиды равны 60°. Найдите площадь боковой поверхности пирамиды.
Решение:
Пусть дана пирамида PABCD, основание которой — ромб ABCD (BD = 24 см, АС = 10 см), 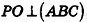
Проведем из точки Р перпендикуляры: 
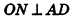
Прямоугольные треугольники РКО, PLO, РМО и PNO равны по катету и противолежащему углу. Отсюда следует, что OK = OL = ОМ = ON. Так как по доказанному эти равные отрезки перпендикулярны сторонам ромба ABCD, то точка О равноудалена от прямых, содержащих стороны ромба, значит, является центром окружности, вписанной в ромб, — точкой пересечения его диагоналей (рис. 112, б).
Треугольники АОВ, ВОС, COD и AOD — ортогональные проекции боковых граней пирамиды АРВ, ВРС, CPD и APD на плоскость основания. По теореме о площади ортогональной проекции многоугольника
Складывая эти равенства, получим: 
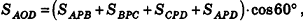
Отсюда 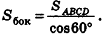
Итак,
Обобщим только что приведенные рассуждения.
Пример: (о пирамиде с равными двугранными углами при основании)
Если все двугранные углы при основании пирамиды равны, то основанием ее высоты является центр окружности, вписанной в основание пирамиды. Докажите.
Решение:
Для данной пирамиды 
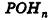
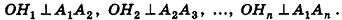
Напомним, что мы рассматриваем только те пирамиды, основаниями которых являются выпуклые многоугольники.
Следует заметить, что если вместо равенства двугранных углов при основании рассматривать равенство углов наклона плоскостей боковых граней пирамиды к плоскости основания, возможна геометрическая ситуация, когда высота пирамиды лежит вне пирамиды. Но рассмотрение таких случаев выходит за пределы нашего курса.
Еще одно важное обобщение решенной задачи касается способа вычисления площади боковой поверхности пирамиды.
Пример: (об ортогональной проекции боковых граней пирамиды на плоскость основания)
Если все двугранные углы при основании пирамиды равны 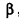
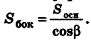
Решение:
Для данной пирамиды 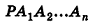
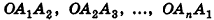
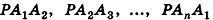
Отсюда
Окончательно получим: 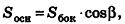
Эту формулу удобно применять, в частности, для вычисления площади боковой поверхности правильной пирамиды.
Аналогично можно доказать следующее утверждение.
Если основание пирамиды состоит из ортогональных проекций нескольких боковых граней, каждая из которых образует с плоскостью основания двугранный угол 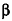
Докажите это утверждение самостоятельно.
Данным фактом можно воспользоваться в задаче п. 9.1, где
Обратим внимание на то, что при решении многих задач, связанных с пирамидами, имеющими описанное выше свойство, отдельно рассматривают прямоугольный треугольник 
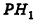
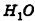
Сечения многогранников
С простейшими случаями сечений тетраэдра и куба вы уже встречались в 10 классе. Придадим представлениям о сечениях геометрических тел определенную математическую строгость.
Секущая плоскость и сечение. Сечения призмы
Пусть в пространстве даны тело и некоторая плоскость. Если хотя бы две точки тела лежат по разные стороны от данной плоскости, то говорят, что плоскость пересекает тело. В таком случае она является секущей плоскостью данного тела. Например, на рисунке 119 плоскость а является секущей плоскостью тела F.
Определение:
Сечением геометрического тела плоскостью называется фигура, состоящая из всех общих точек тела и секущей плоскости.
На рисунке 119 закрашенная фигура является сечением тела F плоскостью а.
Если данное тело — многогранник, то секущая плоскость пересекает его грани по отрезкам. Эти отрезки ограничивают плоский многоугольник, являющийся общей частью данного многогранника и секущей плоскости. Коротко говорят, что сечением многогранника является многоугольник (имея в виду соответствующий плоский многоугольник).
Очевидно, что если многогранник имеет л граней, то количество сторон многоугольника, являющегося сечением данного многогранника, не превышает п. Например, сечением параллелепипеда (он имеет 6 граней) может быть только треугольник, четырехугольник, пятиугольник или шестиугольник. На рисунке 120 сечение куба — шестиугольник ABCDEF.
Для построения сечения многогранника достаточно построить все точки пересечения секущей плоскости с ребрами данного многогранника, после чего соединить отрезками каждые две построенные точки, принадлежащие одной грани. Напомним, что если секущая плоскость пересекает плоскости двух параллельных граней, то прямые пересечения параллельны. Так, на рисунке 120 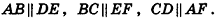
Пример:
Постройте сечение куба 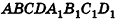
Решение:
Так как точки М и N принадлежат грани 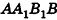
Так как грани куба 
Пусть G — точка пересечения этой прямой с ребром AD (рис. 121, в). Рассуждая аналогично, проводим через точку К прямую, параллельную MN.
Пусть Т — точка пересечения проведенной прямой с ребром CD. Так как точки G и Т принадлежат одной грани ABCD, то отрезок GT — сторона искомого сечения. Следовательно, искомым сечением является пятиугольник MNKTG (рис. 121, г).
Подробнее о построении сечений речь пойдет в п. 10.3. Заметим, что часто задачи на вычисление площадей сечений объединяют в себе задачи на вычисление и на построение: действительно, при решении таких задач необходимо не только вычислить площадь некоторого сечения, но и описать его построение и обосновать, что полученное сечение является искомым.
Пример:
В правильной четырехугольной призме через диагональ одного основания и противолежащую ему вершину другого основания проведено сечение плоскостью Q. Найдите площадь боковой поверхности призмы, если данное сечение образует с плоскостью основания угол а.
Решение:
Пусть дана правильная четырехугольная призма 
Рассуждая аналогично, определяем, что прямые АС и 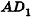
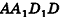
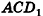
По условию 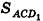
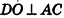
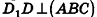
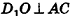
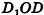
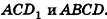
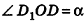
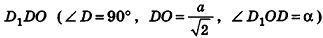
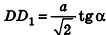
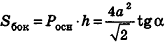
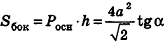
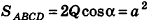
Окончательно получаем:
Ответ:
Рассмотрим подробнее простейшие сечения призм.
Любое сечение призмы плоскостью, параллельной боковому ребру, является параллелограммом. Так, параллелограммом является диагональное сечение призмы — сечение плоскостью, проходящей через боковое ребро и диагональ основания. На рисунке 123 параллелограмм 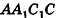
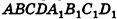
При изучении наклонных призм особую роль играет сечение призмы плоскостью, пересекающей все боковые ребра и перпендикулярной этим ребрам (рис. 124, а). Но существуют наклонные призмы, у которых такого сечения может и не быть. Поэтому будем считать перпендикулярным сечением призмы многоугольник, вершинами которого являются точки пересечения плоскости, перпендикулярной боковым ребрам призмы, с прямыми, содержащими эти ребра (рис. 124, а, б).
Теорема (формула площади боковой поверхности наклонной призмы)
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро:
Пусть перпендикулярное сечение наклонной n-угольной призмы — га-угольник, стороны которого равны 
Сечения пирамиды. Усеченная пирамида
Рассмотрим простейшие сечения пирамид.
Любое сечение пирамиды плоскостью, проходящей через ее вершину, является треугольником. Так, треугольником является диагональное сечение пирамиды — сечение плоскостью, проходящей через вершину пирамиды и диагональ ее основания. На рисунке 125 треугольник PBD — диагональное сечение пирамиды PABCD. Важным случаем сечения пирамиды является сечение, параллельное плоскости основания.
Теорема (о сечении пирамиды, параллельном плоскости основания)
Плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает пирамиду, подобную данной.
Пусть дана пирамида с вершиной Р (рис. 126). Через точку А1 на боковом ребре РА проведена секущая плоскость а, параллельная основанию пирамиды. Рассмотрим гомотетию данной пирамиды с центром Р и коэффициентом 
Рассмотрим теперь другую часть пирамиды, которую отсекает плоскость сечения, параллельная основанию. Эта часть представляет собой многогранник, который называют усеченной пирамидой. Две ее грани (основания усеченной пирамиды) — подобные многоугольники, лежащие в параллельных плоскостях, а остальные грани (боковые грани усеченной пирамиды) — трапеции.
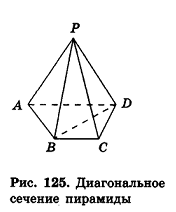
На рисунке 127 изображена усеченная треугольная пирамида 
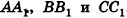
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания. Например, на рисунке 127 высотой усеченной пирамиды является отрезок А1О.
Изображение усеченной пирамиды обычно строят таким образом. Сначала изображают соответствующую полную пирамиду, а затем строят ее сечение плоскостью, параллельной плоскости основания.
Если секущая плоскость правильной пирамиды параллельна основанию, то в результате пересечения получается правильная усеченная пирамида. Основаниями такой пирамиды являются правильные подобные многоугольники, а отрезок, соединяющий центры этих многоугольников, является высотой пирамиды. Очевидно, что боковые ребра правильной усеченной пирамиды равны, значит, ее боковые грани — равнобедренные трапеции. Высоты этих трапеций называются апофемами правильной усеченной пирамиды. Например, на рисунке 128 изображена правильная четырехугольная усеченная пирамида 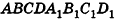
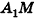
Теорема (формула площади боковой поверхности правильной усеченной пирамиды)
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований на апофему:
Пусть стороны оснований правильной га-угольной усеченной пирамиды с апофемой I равны 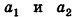
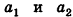
Отсюда площадь боковой поверхности данной усеченной пирамиды 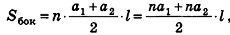
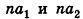
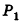
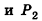
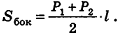
Пример:
Найдите площадь боковой поверхности правильной четырехугольной усеченной пирамиды, если ее диагональное сечение — трапеция с основаниями 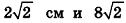
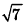
Решение:
Пусть трапеция 
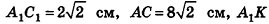
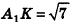
Так как данная пирамида правильная, то трапеция 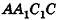
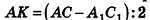
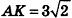
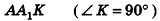
Рассмотрим теперь боковую грань пирамиды — равнобедренную трапецию 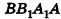
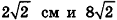
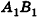

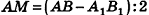
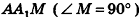
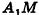
Следовательно,
Ответ:
Следует знать, что для проведения вычислений при решении задач об усеченных пирамидах иногда удобно рассматривать такие фрагменты их сечений:
- фрагмент сечения, проходящего через боковое ребро и центры окружностей, описанных около оснований,— в случае, если боковые ребра пирамиды равны (рис. 130, а, б):
— высота пирамиды,
— радиусы окружностей, описанных около оснований,
— боковое ребро,
— угол наклона бокового ребра к плоскости большего основания;
- фрагмент сечения, проходящего через центры окружностей, вписанных в основания, перпендикулярно ребру основания,— в случае, если боковые грани наклонены к основанию под равными углами (рис. 130, в, г):
— высота пирамиды,
— радиусы окружностей, вписанных в основания,
— высота боковой грани,
— линейный угол двугранного угла при большем основании.
Заметим также, что при решении некоторых задач целесообразно достроить данную усеченную пирамиду до полной.
Построение сечений многогранников
При решении задач на построение сечений многогранников часто возникает необходимость построить прямую пересечения секущей плоскости с плоскостью грани многогранника. Такую прямую называют следом секущей плоскости на плоскости данной грани. След легко построить, если известны две точки плоскости данной грани, принадлежащие секущей плоскости. Но такие точки не всегда даны — для их нахождения применяют специальный метод следов.
Рассмотрим данный метод на примере уже известной вам задачи из п. 10.1.
Пусть требуется построить сечение куба 
Построим теперь точку пересечения прямой MN с плоскостью основания ABC. Для этого определим прямую пересечения грани 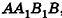
Так как точки М и G принадлежат грани 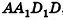
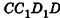
Как видим, самый «тонкий» момент применения метода следов — построение точки пересечения прямой, принадлежащей секущей плоскости, с плоскостью грани многогранника. Для этого используют известное свойство параллельного проектирования: проекцией прямой является прямая, причем если данная прямая не параллельна плоскости проекции, то она пересекается со своей проекцией. Обобщим различные случаи таких построений для призмы и пирамиды, представив их в виде таблицы.
Построение точки X пересечения прямой АВ с плоскостью основания многогранника
Заметим, что метод следов не всегда удобно применять, если построенная прямая сечения «почти параллельна» плоскости основания многогранника (то есть пересекает ее под углом, близким к 0°),— в таком случае искомая точка пересечения X может выйти за пределы рисунка.
Рассмотрим еще один метод, с помощью которого можно строить сечения многогранников, не выходя за их пределы.
Пусть требуется построить сечение четырехугольной пирамиды PABCD плоскостью, проходящей через точки М, N и К на. ребрах пирамиды (рис. 132, а). Сначала, как и в предыдущих случаях, построим отрезки MN и NK, которые являются сторонами искомого сечения. Но для построения точки пересечения секущей плоскости MNK с ребром PC применим метод, отличный от метода следов.
Проведем диагонали основания АС и BD и обозначим точку их пересечения Т. Соединим полученную точку Т с вершиной пирамиды Р (рис. 132, б). Плоскость диагонального сечения PJBD и секущая плоскость MNK имеют общие точки М и К, а значит, пересекаются по прямой МК. Прямые МК и РТ пересекаются (объясните почему) в некоторой точке Т1 (рис. 132, в), также принадлежащей секущей плоскости MNK.
Аналогично плоскости РАС и MNK имеют общие точки N и T1 а значит, пересекаются по прямой NT1. Прямая NT1 пересекает ребро PC в некоторой точке L (рис. 132, г), которая также является общей точкой плоскостей MNK и РАС, а следовательно, принадлежит искомому сечению. Соединив точку L с точками М и К, получим искомое сечение MNKL.
Описанный метод построения сечений называют методом внутреннего проектирования или методом проекций. Такое название несложно объяснить: действительно, точка Т основания пирамиды является проекцией точки сечения Т1 на плоскость основания в направлении прямой РТ; таким образом, получив сначала проекцию точки Т1 мы восстановили и саму точку.
Правильные многогранники
Как известно, в планиметрии для любого натурального числа га, не меньшего 3, существует правильный n-угольник — многоугольник, в котором все стороны равны и все углы равны. Пространственными аналогами правильных многоугольников являются правильные многогранники.
Виды правильных многогранников
Определение:
Правильным многогранником называется выпуклый многогранник, у которого все грани являются равными правильными многоугольниками и в каждой вершине сходится одинаковое число ребер.
Примером правильного многогранника является куб: все его грани — равные квадраты, а в каждой вершине сходится по три ребра.
Из данного определения следует, что все ребра правильного многогранника равны. Можно также доказать, что все двугранные углы правильного многогранника, содержащие две грани с общим
С древних времен человечеству были известны пять видов правильных многогранников, причем доказано, что других видов правильных многогранников не существует. Прежде чем рассмотреть каждый вид отдельно, обоснуем, что гранями правильного многогранника могут быть только треугольники, четырехугольники или пятиугольники. Действительно, при 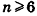
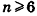
Перейдем к описанию каждого из пяти видов правильных многогранников.
Правильный тетраэдр — это многогранник, поверхность которого состоит из четырех равносторонних треугольников (рис. 138). В каждой вершине правильного тетраэдра сходится по три ребра. Заметим, что правильный тетраэдр является правильной треугольной пирамидой, у которой боковые ребра равны ребрам основания.
Куб (правильный гексаэдр) — шестигранник, поверхность которого состоит из шести квадратов (рис. 139). В каждой вершине куба сходится по три ребра. Напомним, что куб является правильной четырехугольной призмой, у которой боковые ребра равны ребрам основания.
Правильный октаэдр — восьмигранник, гранями которого являются равносторонние треугольники (рис. 140). В отличие от правильного тетраэдра, в каждой вершине правильного октаэдра сходится по четыре ребра.
Правильный додекаэдр — многогранник, поверхность которого состоит из двенадцати правильных пятиугольников (рис. 141). Каждая вершина правильного додекаэдра является вершиной трех правильных пятиугольников, то есть из нее выходит по три ребра.
Правильный икосаэдр — многогранник, поверхность которого состоит из двадцати равносторонних треугольников (рис. 142). Каждая вершина правильного икосаэдра является вершиной пяти правильных треугольников, то есть в ней сходится по пять ребер.
Рассмотрим элементы симметрии некоторых правильных многогранников.
Правильный тетраэдр не имеет центра симметрии. Осью симметрии этого многогранника является прямая, проходящая через середины двух скрещивающихся ребер. Таким образом, правильный тетраэдр имеет три оси симметрии (рис. 143, а). Плоскость симметрии правильного тетраэдра проходит через его ребро перпендикулярно скрещивающемуся с ним ребру (рис. 143, б). Итак, правильный тетраэдр имеет шесть плоскостей симметрии.
Куб имеет один центр симметрии — точку пересечения его диагоналей. Осями симметрии куба являются прямые, проходящие через центры двух противолежащих граней (таких прямых три), и прямые, проходящие через середины двух параллельных ребер, не принадлежащих одной грани (таких прямых шесть). Итак, куб имеет девять осей симметрии, каждая из которых проходит через его центр симметрии (рис. 144, а).
Плоскостями симметрии куба являются три плоскости, каждая из которых проходит через середины четырех параллельных ребер, и шесть плоскостей, проходящих через пару параллельных ребер, не принадлежащих одной грани. Таким образом, куб имеет девять плоскостей симметрии (рис. 144, б).
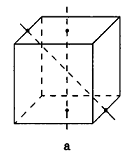
Остальные правильные многогранники имеют центр симметрии и несколько осей и плоскостей симметрии (попробуйте определить их число самостоятельно).
Свойства правильных многогранников издавна привлекают ученых, строителей, архитекторов, ювелиров. Великий древнегреческий философ Платон связывал с правильными многогранниками четыре природные стихии: с правильным тетраэдром — Огонь, с кубом — Землю, с правильным октаэдром — Воздух, с правильным додекаэдром — Воду. Он высказал гипотезу о том, что существует еще одна, пятая стихия, связанная с правильным икосаэдром, — Божественный эфир. И хотя эта гипотеза была позднее опровергнута наукой, исследования Платона по-прежнему вызывают интерес как одна из первых попыток математического моделирования в естествознании, а сами правильные многогранники и сегодня называют Платоновыми телами.
Совершенные формы правильных многогранников не могли не отобразиться на полотнах знаменитых художников. На рисунке 145 вы видите гравюру М. Эшера «Звезды», среди элементов которой есть правильные многогранники.
Полуправильные многогранники. Другие виды многогранников
Достаточно жесткие условия определения правильных многогранников существенно ограничивают их число. Поэтому наряду с правильными многогранниками внимание исследователей привлекают также и те, которые удовлетворяют условиям определения правильного многогранника лишь частично. Это, например, полуправильные многогранники — выпуклые многогранники, гранями которых являются правильные многоугольники нескольких видов, а в каждой вершине сходится одинаковое число ребер.
Среди известных вам видов многогранников к полуправильным относятся правильные n-угольные призмы, боковые ребра которых равны ребрам основания (за исключением куба, являющегося правильным многогранником). На рисунке 146 изображена правильная шестиугольная призма, все боковые грани которой — квадраты; такая призма является полуправильным многогранником. К полуправильным многогранникам относятся и так называемые антипризмы, основаниями которых являются равные правильные n-угольники, а боковыми гранями — равносторонние треугольники (рис. 147).
Кроме этих двух бесконечных серий — призм и антипризм, существует еще 14 видов полуправильных многогранников, 13 из которых открыл и описал Архимед (их называют телами Архимеда), а четырнадцатый был открыт только в XX веке.
Охарактеризуем тела Архимеда, изображенные на рисунке 148. Самые простые из них можно получить путем «срезания» углов правильных многогранников плоскостями. Например, срезав углы правильного тетраэдра так, чтобы каждая секущая плоскость отсекала третью часть его ребер, выходящих из одной вершины, получим усеченный тетраэдр (рис. 148, а).
Аналогичным образом, срезав углы правильных октаэдра и икосаэдра, получим усеченный октаэдр (рис. 148, б) и усеченный икосаэдр (рис. 148, в) — последний многоугольник напомнит многим из вас футбольный мяч. Так же из куба получают усеченный куб (рис. 148, г), а из правильного додекаэдра — усеченный додекаэдр (рис. 148, д).
Если в кубе провести секущие плоскости через середины ребер, выходящих из одной вершины, то в результате отсекания этими плоскостями частей куба получим кубооктаэдр (рис. 148, е). Его название объясняется тем, что он имеет шесть граней-квадратов (как куб) и восемь граней — правильных треугольников (как правильный октаэдр). Если указанным способом отсечь углы правильного додекаэдра, получим икосододекаэдр (рис. 148, ж).
К последним двум многогранникам можно снова применить операцию срезания углов. В результате получим еще два полуправильных многогранника — усеченный кубооктаэдр (рис. 148, з) и усеченный икосододекаэдр (рис. 148, и).
Другие четыре архимедовых тела — это ромбокубооктаэдр (рис. 148, к), ромбоикосододекаэдр (рис. 148, л), плосконосый куб (рис. 148, м) и плосконосый додекаэдр (рис. 148, н)*.
И, наконец, единственный полуправильный многогранник, открытый не Архимедом,— это псевдоромбокубооктаэдр (рис. 149). Его открыл в 1950 году немецкий математик Й. Миллер, а немного позднее, независимо от него и друг от друга,-г советские ученые В. Ашкинузе и Л. Есаулова.
Форму полуправильных многогранников ювелиры часто придают драгоценным камням при огранке (рис. 150).
Среди других видов многогранников большую эстетическую и декоративную ценность представляют звездчатые многогранники — невыпуклые многогранники, гранями которых являются
правильные многоугольники. Особенно выделяются правильные звездчатые многогранники — так называемые тела Кеплера — Пуансо. Их всего четыре (рис. 151). Такие многогранники можно получить из правильных додекаэдра и икосаэдра продолжением их ребер или граней.
Многочисленные формы звездчатых многогранников созданы самой природой: например, такие формы имеют снежинки (рис. 152). С давних пор ученые занимались исследованием их форм. Сейчас известно несколько тысяч видов снежинок.
Большое значение в химии и кристаллографии имеют другие природные многогранники — параллелоэдры. Это выпуклые многогранники, которыми можно заполнить пространство так, чтобы они не входили друг в друга и не оставляли между собой пустот. Пять типов параллелоэдров открыл в 1881 году один из основателей кристаллографии русский ученый Е. С. Федоров, в честь которого эти многогранники были названы телами Федорова (рис. 153). А знаменитая теорема теории параллелоэдров носит имя выдающегося украинского математика Георгия Феодосьевича Вороного (1868-1908). Вообще кристаллография как наука многим обязана геометрии, ведь физические свойства кристаллов зависят от структуры их кристаллических решеток, а те, в свою очередь, состоят из многогранников (рис. 154).
Справочный материал
Двугранные и многогранные углы
Двугранным углом называется фигура, состоящая из двух полуплоскостей (граней двугранного угла) с общей граничной прямой (ребром двугранного угла).
Угол АОВ — линейный угол двугранного угла.
Все линейные углы двугранного угла равны.
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Трехгранным углом называется фигура, состоящая из трех плоских углов с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости.
Многогранники
Многогранником называется тело, поверхность которого состоит из конечного числа плоских многоугольников.
Плоские многоугольники, из которых состоит поверхность многогранника, называются гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника.
Выпуклым многогранником называется многогранник, все точки которого лежат по одну сторону от плоскости каждой его грани или в самой этой плоскости.
Призмы
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников
Многоугольники называют основаниями призмы. Все грани призмы, не являющиеся основаниями, называют боковыми гранями призмы
- Основания призмы параллельны и равны
- Боковые грани призмы — параллелограммы
Боковыми ребрами призмы называются отрезки, соединяющие соответствующие вершины оснований.
- Боковые ребра призмы параллельны и равны.
Высотой призмы называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания
Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани
Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности — сумма площадей ее боковых граней.
Виды призм
Прямой призмой называется призма, боковые ребра которой перпендикулярны плоскостям оснований
Площадь боковой поверхности прямой призмы равна произведению периметра ее основания на высоту:
Наклонной призмой называется призма, которая не является прямой
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного свечения на боковое ребро:
Правильной призмой называется прямая призма, основания которой — правильные многоугольники
Параллелепипедом называется призма, основание которой — параллелограмм
- Противолежащие грани параллелепипеда параллельны и равны
- Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам
- Точка пересечения диагоналей параллелепипеда — центр его симметрии
Прямым параллелепипедом называется прямая призма, основанием которой является параллелограмм
Прямоугольным параллелепипедом называется прямой параллелепипед, основанием которого является прямоугольник
Пространственная теорема Пифагора. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:
Кубом называется прямоугольный параллелепи-у которого все ребра равны вершина
Пирамиды
Пирамидой называется многогранник, который состоит из плоского многоугольника (основания пирамиды), точки, не лежащей в плоскости основания (вершины пирамиды), и всех отрезков, соединяющих вершину с точками основания
Тетраэдром называют треугольную пирамиду
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания
Площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней, а площадью полной поверхности — сумма площадей основания и боковой поверхности:
Виды пирамид
Правильной пирамидой называется пирамида, основанием которой является правильный многоугольник, а основание высоты пирамиды совпадает с центром этого многоугольника
Апофемой правильной пирамиды называется высота боковой грани, проведенная из вершины пирамиды
- Все боковые ребра правильной пирамиды равны
- Все боковые ребра правильной пирамиды равно-наклонены к плоскости основания
- Все боковые ребра правильной пирамиды обра-! зуют равные углы с высотой пирамиды
- Все боковые грани правильной пирамиды — равные равнобедренные треугольники
- Все двугранные углы при основании правильной пирамиды равны
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра ее основания на апофему:
Усеченная пирамида
Плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает пирамиду, подобную данной, и многогранник, который называют усеченной пирамидой.
Основаниями усеченной пирамиды являются основание данной пирамиды и подобный ему многоугольник, полученный в сечении.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.
Если секущая плоскость правильной пирамиды параллельна основанию, то в результате пересечения получается правильная усеченная пирамида.
Апофемой правильной усеченной пирамиды называется высота боковой грани
- Основания — правильные многоугольники.
- Отрезок, соединяющий центры оснований,— высота.
- Боковые грани — равные равнобедренные трапеции Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований на апофему:
Историческая справка
Многогранники как наиболее распространенные геометрические тела интересовали ученых издавна. В разные эпохи математики предлагали собственные определения призмы и пирамиды. В результате возникло несколько подходов к определению многогранника — в частности, многогранник рассматривают либо как поверхность, либо как тело, ограниченное поверхностью. Каждый из этих подходов корректен с научной точки зрения и имеет своих сторонников.
Учение о правильных многогранниках изложено в последней книге знаменитых «Начал» Евклида, но некоторые историки приписывали первенство в исследовании правильных многогранников Пифагору. Между тем, почти все известные древнегреческие геометры так или иначе затрагивали в своих работах свойства правильных многогранников. В Средние века большой интерес к этой теме проявили художники и архитекторы.
Выдающийся немецкий астроном и математик Иоганн Кеплер (1571-1630) на основании теории правильных многогранников построил модель Солнечной системы (так называемый «кубок Кеплера»). Правда, в дальнейших исследованиях астрономов гипотезы Кеплера не нашли подтверждения. Но идея использования многогранников для моделирования природных явлений дала толчок многим исследованиям в разных областях науки.
Тела вращения
Глубокое изучение природы является дающим жизнь источником математических открытий.
Жан Батист Фурье, французский математик
Многочисленные геометрические объекты и даже направления геометрических исследований ученым подсказывает сама природа. Так, множество созданных ею предметов имеют форму тел вращения.
В этой главе мы рассмотрим три классических тела вращения — цилиндр, конус и шар. Все они являются лишь абстрактными моделями реальных предметов, окружающих нас в повседневной жизни, но общие исследовательские подходы к их изучению и полученные результаты могут быть использованы в архитектуре, искусстве, технике.
Изучение тел вращения опирается на известные из курса планиметрии свойства окружностей и многоугольников. В процессе усвоения нового материала вам помогут также модели рассматриваемых тел, которые вы можете изготовить своими руками.
Цилиндр
При вращении вокруг оси I на угол 360° произвольная точка М, не принадлежащая прямой I, описывает окружность (рис. 157, а). Центр этой окружности О лежит на прямой I, а сама окружность — в плоскости, проходящей через точку М и перпендикулярной прямой I.
Поверхности и тела вращения
Рассмотрим теперь линию т, которая лежит в одной плоскости с прямой ! и не пересекает ее. При вращении вокруг прямой I каждая точка линии т описывает окружность с центром на этой прямой. Линия т при таком вращении описывает некоторую поверхность (рис. 157, б). Эту поверхность называют поверхностью вращения.
Вернемся к рисунку 157, а и рассмотрим вращение вокруг прямой I отрезка ОМ, -один из концов которого принадлежит этой прямой. При таком вращении получается круг с центром О и радиусом ОМ. Тогда при вращении вокруг прямой I плоской фигуры 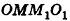
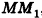
Очевидно, что любое сечение тела вращения плоскостью, перпендикулярной его оси, является кругом. Рассмотрим сечение тела вращения плоскостью, проходящей через его ось. Такое сечение называется осевым. На рисунке 158 шестиугольник ABCDEF — осевое сечение тела вращения. Данное тело получено вращением плоского пятиугольника АВСКМ вокруг прямой, содержащей сторону КМ.
Далее вместо слов «плоский многоугольник вращается вокруг прямой, содержащей его сторону», мы будем говорить ♦многоугольник вращается вокруг стороны».
Форму тел вращения имеют элементы архитектурных сооружений, многие технические детали, различные виды посуды и т. д. (рис. 159). Заметим, что дать определение любого тела вращения можно двумя способами — через описание самого тела или через описание способа его получения вращением плоской фигуры вокруг оси (о видах определений речь пойдет в п.12.3). В дальнейшем мы будем придерживаться более традиционного, первого, способа определения, но также указывать, как получить данную фигуру вращением.
Определение:
Цилиндром (точнее, круговым цилиндром) называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей, ограничивающих основания,— образующими цилиндра.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. Так как в школьном курсе мы будем рассматривать только прямые круговые цилиндры, в дальнейшем договоримся называть их просто цилиндрами.
Радиусом, цилиндра называется радиус его основания.
Высотой цилиндра называется перпендикуляр, проведенный из точки одного основания цилиндра к плоскости другого основания. Очевидно, что высота цилиндра равна его образующей.
На рисунке 160 изображен цилиндр с центрами оснований 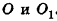
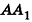
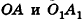
Рассмотрим некоторые свойства цилиндра.
Так как параллельный перенос является движением, то основания цилиндра — равные круги, лежащие в параллельных плоскостях.
Из свойств параллельного переноса следует и то, что образующие цилиндра параллельны и равны.
Цилиндр является телом вращения, которое получается вращением прямоугольника вокруг его стороны. Например, на рисунке 160 изображен цилиндр, полученный вращением прямоугольника 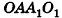
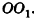
Цилиндрические формы часто встречаются в архитектуре, технике, спорте и в быту (рис. 161).
Рассмотрим некоторые виды сечений цилиндра. Сечение цилиндра плоскостью, параллельной плоскости основания, представляет собой круг, равный основанию. Действительно, параллельный перенос на вектор 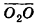
Так как образующие цилиндра параллельны друг другу и его оси, равны и перпендикулярны основаниям, то сечение цилиндра плоскостью, параллельной его оси, является прямоугольником (рис. 162, б). Две стороны этого прямоугольника — образующие цилиндра, а две другие — параллельные хорды его оснований. Осевое сечение цилиндра также является прямоугольником (рис. 162, в), две стороны которого — образующие цилиндра, а две другие — параллельные диаметры его оснований.
В случае, когда высота цилиндра равна диаметру его основания, осевое сечение цилиндра является квадратом, а сам цилиндр называется равносторонним.
Плоскость осевого сечения является плоскостью симметрии цилиндра (обоснуйте этот факт самостоятельно).
Плоскость, проходящая через образующую цилиндра и перпендикулярная осевому сечению, содержащему эту образующую, называется касательной плоскостью к цилиндру. Плоскость 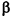
Пример №223
Радиус цилиндра равен 5 см. Площадь сечения, параллельного оси цилиндра и удаленного от нее на 4 см, равна 42 см 2 . Найдите высоту цилиндра.
Решение:
Пусть дан цилиндр с осью 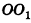
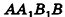
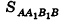
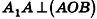
Проведем в плоскости АОВ перпендикуляр ОС к прямой АВ. Тогда 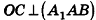
Проведем радиусы цилиндра OA и ОВ. Отрезок ОС — медиана и высота равнобедренного треугольника АОВ. Таким образом, из треугольника АОС 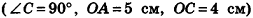
Следовательно, 
Виды определений
Как мы уже отмечали, в геометрии существуют разные подходы к определению основных фигур. Разные способы определения понятий используются и в других науках. Опишем наиболее распространенные виды определений.
Определение как логическая операция должно решать две задачи — выделять определяемый предмет и отличать его от всех других. Поэтому большинство научных определений — это определения, данные через ближайший род и видовое отличие (в логике такие определения называют классическими). Поясним особенности классического определения на примере известного вам определения куба: «Кубом называется прямоугольный параллелепипед, у которого все ребра равны». В этом определении сначала выделяется ближайший род многогранников, к которому относится куб, — прямоугольные параллелепипеды, а затем описывается отличие куба от остальных прямоугольных параллелепипедов, — равенство всех ребер.
К классическим относится и большинство определений в естественных и гуманитарных науках. Например, в филологии архаизмом называется устарелое слово, вышедшее из общего употребления. Для этого определения архаизма используется ближайший род («слово») и видовое отличие, заключающееся в устарелости данного слова.
Разновидностью классических являются так называемые генетические определения, в которых видовое отличие описывает способ образования определяемого предмета. Например, вместо определения цилиндра, приведенного в п. 12.2, можно было бы дать равносильное генетическое определение: «Цилиндром называется тело, которое получается при вращении прямоугольника вокруг его стороны».
Кроме определений, явно указывающих на тождество двух понятий — определяемого и того, которое определяет, существуют и другие, неявные определения. Вспомним, например, определение пирамиды: «Пирамидой называется многогранник, который состоит из плоского многоугольника (основания пирамиды), точки, не лежащей в плоскости основания (вершины пирамиды), и всех отрезков, соединяющих вершину с точками основания». В контексте этого определения мы описали, кроме пирамиды, еще два понятия — основание пирамиды и вершина пирамиды, иначе говоря, дали контекстуальное определение этих двух понятий.
Другим видом неявных определений являются определения путем показа. Представим, например, что нам нужно объяснить собеседнику, какой цвет называется «индиго». Конечно, наиболее действенный способ объяснения — показать предмет или изображение определяемого цвета. Определения путем показа в логике называют остенсивными. Так, в курсе геометрии мы использовали остенсивные определения для отдельных видов полуправильных и звездчатых многогранников (п. 11.2).
В науке, учебе, повседневной жизни в зависимости от конкретной ситуации целесообразными могут оказаться разные виды определений. Но главная цель, с которой они используются, всегда остается неизменной — определения должны способствовать процессу общения между людьми, помогать им лучше понимать друг друга. Недаром знаменитый древнегреческий философ Сократ говорил, что благодаря правильным определениям он продолжает дело своей матери-акушерки, помогая рождению истины в споре.
Конус
Определение:
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга (основания конуса), точки, не принадлежащей плоскости этого круга (вершины конуса), и всех отрезков, соединяющих вершину конуса с точками основания.
Конус и его элементы
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус называется прямым, если прямая, проходящая через вершину конуса и центр окружности основания, перпендикулярна плоскости основания (рис. 166). Так как в школьном курсе будут рассматриваться только прямые круговые конусы, в дальнейшем договоримся называть их просто конусами.
На рисунке 166 изображен конус с вершиной Р и центром основания О. Отрезок РА — образующая этого конуса, а отрезок OA — радиус его основания (или радиус конуса).
Высотой конуса называется перпендикуляр, проведенный из вершины конуса к плоскости основания. Очевидно, что в конусе высота соединяет вершину с центром основания. Например, на рисунке 166 высотой конуса является отрезок РО.
Все образующие конуса являются наклонными к плоскости основания, которые проведены из вершины конуса и имеют равные проекции. Отсюда следует, что все образующие конуса равны и составляют равные углы с плоскостью основания.
Конус является телом вращения, которое получается вращением прямоугольного треугольника вокруг его катета. Например, на рисунке 166 изображен конус, полученный вращением прямоугольного треугольника РОА вокруг катета РО. Таким образом, прямая, содержащая высоту конуса, является его осью.
Формы конусов (иначе их называют коническими формами) имеют многие тела, встречающиеся в природе и технике, в архитектуре и быту (рис. 167).
В физике, строительстве, сельском хозяйстве и горном деле используется понятие угла естественного уклона сыпучего материала, то есть угла наклона образующей к плоскости основания конуса, который образуется свободной поверхностью насыпи (рис. 168). Этот угол связан с коэффициентом трения и зависит от состава, формы, влажности и удельного веса материала (для песка он составляет от 20° до 40°, для грунта — от 17° до 55°, для зерна — от 20° до 30°). По углу естественного уклона определяют, в частности, максимально допустимые углы скоса карьеров, насыпей, штабелей и т. п.
Сечения конуса. Усеченный конус
Рассмотрим некоторые виды сечений конуса. Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, боковые стороны которого — образующие данного конуса (рис. 169, а). В частности, равнобедренным треугольником является осевое сечение конуса (рис. 169, б), причем высотой этого треугольника служит высота конуса, а основанием — диаметр основания конуса.
Если диаметр основания конуса равен образующей, то осевое сечение конуса — равносторонний треугольник; такой конус называется равносторонним. Плоскость осевого сечения является плоскостью симметрии конуса (обоснуйте этот факт самостоятельно).
Плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащего эту образующую, называется касательной плоскостью к конусу. Плоскость р на рис. 169, б является касательной к конусу.
Отдельного рассмотрения заслуживает сечение конуса, параллельное плоскости основания.
Теорема (о сечении конуса, параллельном плоскости основания)
Сечение конуса плоскостью, параллельной плоскости основания, является кругом, центр которого лежит на оси конуса. Образующая и высота конуса делятся плоскостью этого сечения на пропорциональные части.
Пусть плоскость а, параллельная плоскости основания конуса, пересекает его высоту РО в точке 
Рассмотрим преобразование гомотетии с центром Р, которое переводит плоскость основания конуса в плоскость а. Оно совмещает основание конуса с его сечением плоскостью а, а точку О — с точкой 
Рассмотрим теперь треугольники 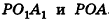
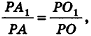
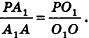
Площадь сечения конуса, параллельного плоскости основания, и площадь основания относятся как квадраты расстояний от вершины конуса до плоскостей сечения и основания.
Таким образом, плоскость, параллельная плоскости основания конуса и пересекающая его образующие, отсекает конус, подобный данному, и тело, которое называется усеченным конусом. Основание данного конуса и круг, полученный в сечении, называются основаниями усеченного конуса, а перпендикуляр, проведенный из точки одного основания к плоскости другого основания,— высотой усеченного конуса. Очевидно, что высотой усеченного конуса является, в частности, отрезок, соединяющий центры его оснований. Отрезки образующих данного конуса, ограниченные плоскостями оснований усеченного конуса, называются образующими усеченного конуса. Все образующие усеченного конуса равны и наклонены к плоскости каждого из оснований под равными углами (объясните почему).
На рисунке 171 изображен усеченный конус с высотой 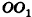
Усеченный конус является телом, которое получается вращением прямоугольной трапеции вокруг ее меньшей боковой стороны. Так, на рисунке 171 изображен усеченный конус, полученный вращением прямоугольной трапеции 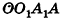
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, основаниями которой являются диаметры оснований усеченного конуса, а боковыми сторонами — его образующие. Так, на рисунке 172 осевое сечение усеченного конуса — равнобедренная трапеция
Пример №224
Радиусы оснований усеченного конуса равны R и г (R>r), а образующая наклонена к плоскости основания под углом 45°. Найдите площадь осевого сечения.
Решение:
Пусть равнобедренная трапеция 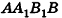
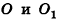
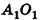
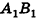
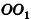
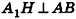
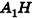
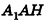
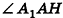
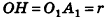
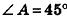
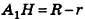
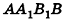
Ответ:
Заметим, что в некоторых задачах об усеченных конусах целесообразно рассматривать полный конус, из которого получен данный усеченный конус.
Шар и сфера
Как известно, множество всех точек плоскости, удаленных от данной точки на расстояние, не превышающее заданное, называется кругом. В пространстве все точки, обладающие аналогичным свойством, образуют шар (рис. 176, а).
Определение:
Шаром называется множество всех точек пространства, удаленных от данной точки на расстояние, не превышающее заданное.
Данную точку называют центром шара, а заданное расстояние — радиусом шара.
Сферой называется поверхность шара.
Таким образом, сфера состоит из всех точек пространства, удаленных от центра шара (он является также и центром сферы) на заданное расстояние R (радиус сферы). Радиусом шара (сферы) называется также любой отрезок, соединяющий центр с точкой сферы. На рисунке 175, а таким является отрезок OA.
Отрезок, соединяющий две точки сферы, называется хордой сферы. Хорда, проходящая через центр сферы, называется диаметром шара (сферы). Концы диаметра называются диаметрально противоположными точками. На рисунке 175, а точки А и В — диаметрально противоположные точки сферы, АВ — диаметр шара (сферы).
Шар является телом вращения, которое получается вращением полукруга вокруг его диаметра (рис. 175, б).
Рассматривая взаимное расположение шара и плоскости в пространстве, целесообразно провести аналогию с расположением круга и прямой на плоскости (рис. 176, а-в). Три случая расположения шара относительно плоскости определяются соотношением между радиусом шара и расстоянием от его центра до плоскости:
- если расстояние от центра шара до плоскости больше радиуса шара, то шар и плоскость не имеют общих точек (рис. 177, а): действительно, если
, то для любой точки М плоскости а
то есть плоскость а не содержит точек шара;
- если расстояние от центра шара до плоскости равно радиусу шара, то плоскость имеет с шаром (и сферой, которая его ограничивает) единственную общую точку (рис. 177, б): в этом случае для произвольной точки М плоскости а, которая не совпадает с А, ОМ > OA = R, то есть плоскость а имеет с шаром единственную общую точку А (более подробно этот случай будет рассмотрен в п. 14.2);
- если расстояние от центра шара до плоскости меньше радиуса шара, то шар и плоскость пересекаются по кругу (рис. 177, в).
Рассмотрим последний случай подробно.
Теорема (о сечении шара)
Если расстояние от центра шара до плоскости меньше радиуса шара, то сечение шара данной плоскостью является кругом. Центр этого круга находится в основании перпендикуляра, проведенного из центра шара к плоскости сечения.
Пусть а — секущая плоскость шара с центром О и радиусом R, 
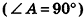
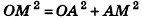
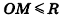
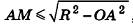
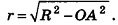
Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью является окружностью. Центр этой окружности находится в основании перпендикуляра, проведенного из центра сферы к плоскости сечения.
Заметим, что в случае, когда секущая плоскость проходит через центр шара (такая плоскость называется диаметральной), центры шара и сечения совпадают, а радиус сечения равен радиусу шара (рис. 179).
Любая диаметральная плоскость шара является его плоскостью симметрии (докажите это самостоятельно).
Сечение шара диаметральной плоскостью называется большим кругом, а окружность этого сечения — большой окружностью.
На географическом глобусе линия экватора представляет собой большую окружность (рис. 180, а). Географические параллели — это линии сечений поверхности Земли плоскостями, параллельными плоскости экватора, а градусы северной и южной широты указывают угол между соответствующими радиусами земного шара — например, город Харьков находится на 50° северной широты (рис. 180, б).
Пример №225
Через конец радиуса шара проведена плоскость под углом 45° к данному радиусу. Найдите площадь получившегося сечения, если радиус шара равен 6 см.
Решение:
Пусть круг с центром 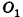
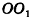
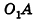
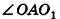
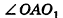
Из треугольника
Искомая площадь S равна 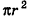
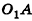
Ответ:
Касательная плоскость к сфере
Рассмотрим более подробно случай, когда шар и плоскость имеют единственную общую точку.
Определение:
Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой единственную общую точку.
Общая точка касательной плоскости и сферы называется точкой касания. На рисунке 182 плоскость а касается сферы (шара) с центром О в точке А.
Определим взаимное расположение касательной плоскости и радиуса сферы, проведенного в точку касания.
Теорема (свойство касательной плоскости)
Касательная плоскость к сфере перпендикулярна радиусу сферы, проведенному в точку касания.
Пусть плоскость а касается сферы с центром О в точке А (рис. 183). Докажем методом от противного, что 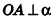
Если это не так, то отрезок OA является наклонной к плоскости а. Проведем перпендикуляр ОВ к плоскости а. Очевидно, что ОВ
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.












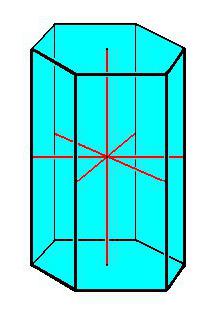
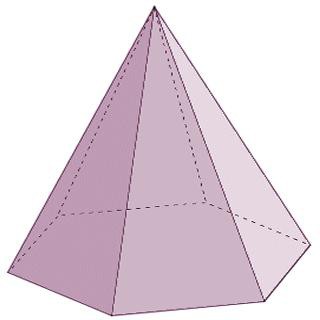


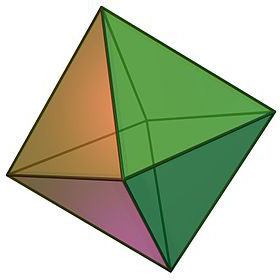
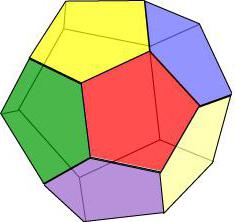
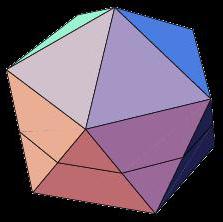

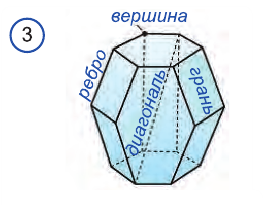
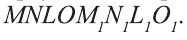
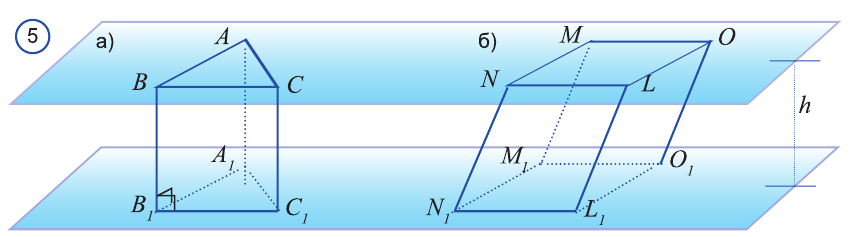
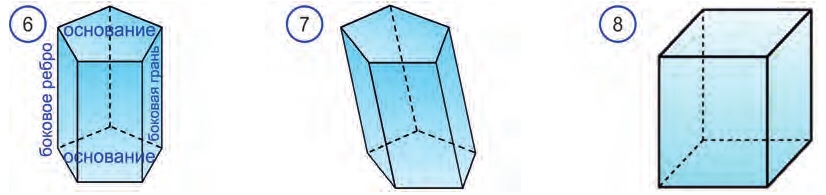
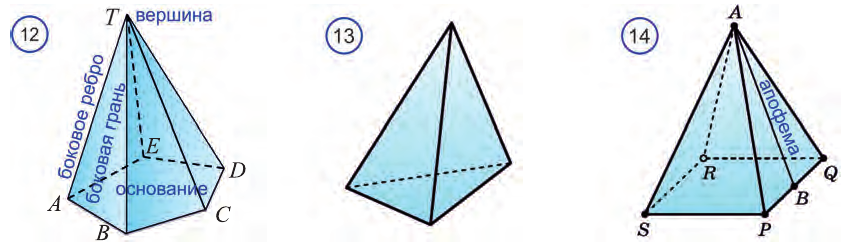
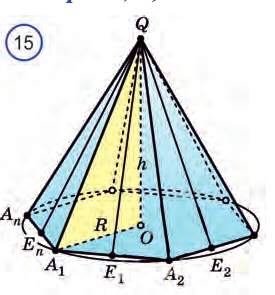

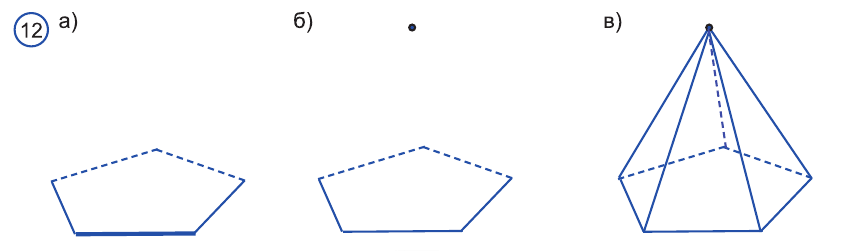
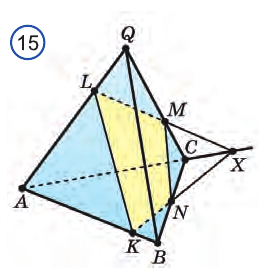
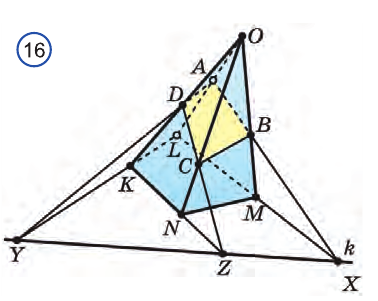
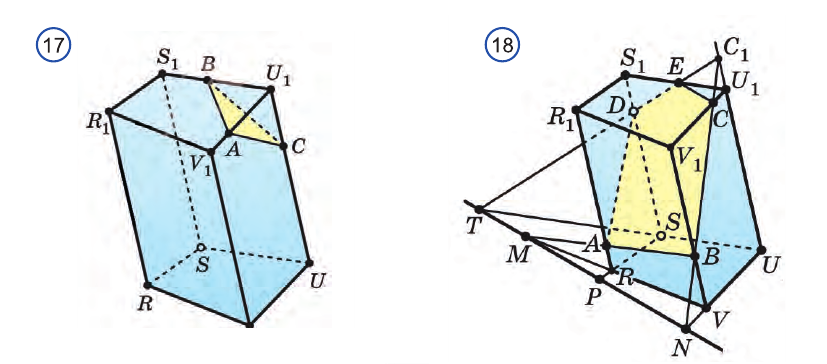
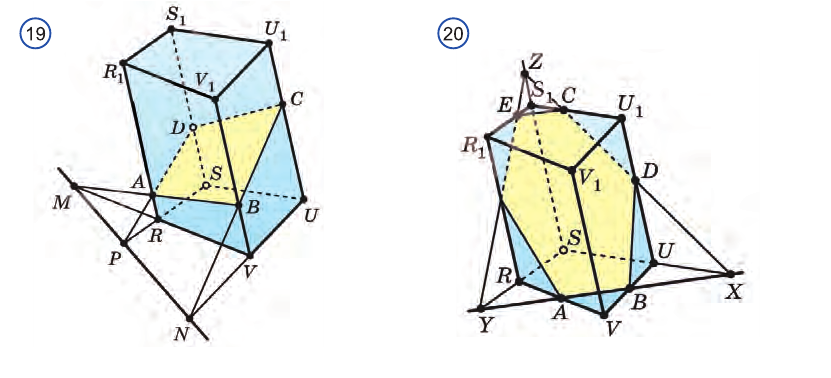

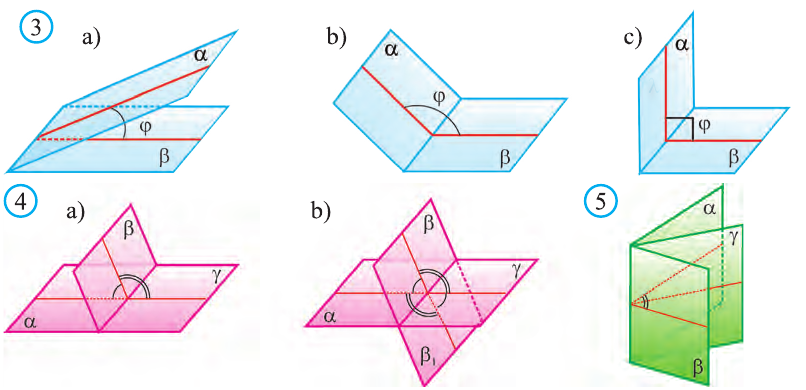
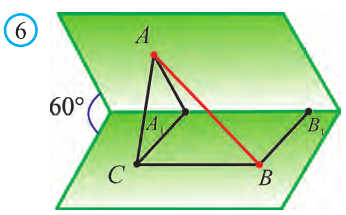
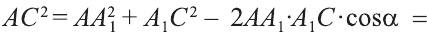
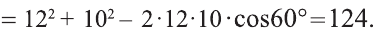
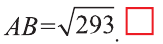
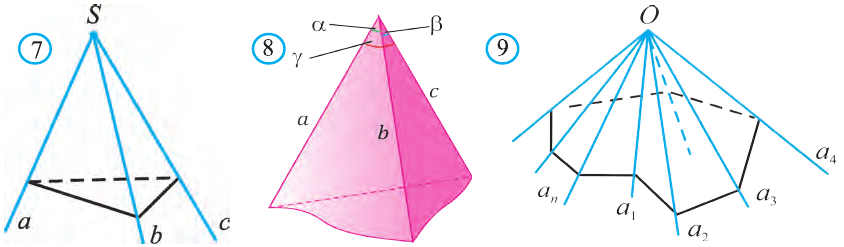
 и сумма плоских углов трёхгранного угла меньше 360 о :
и сумма плоских углов трёхгранного угла меньше 360 о : 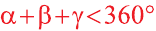 .
.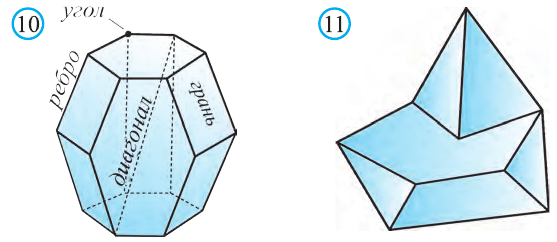
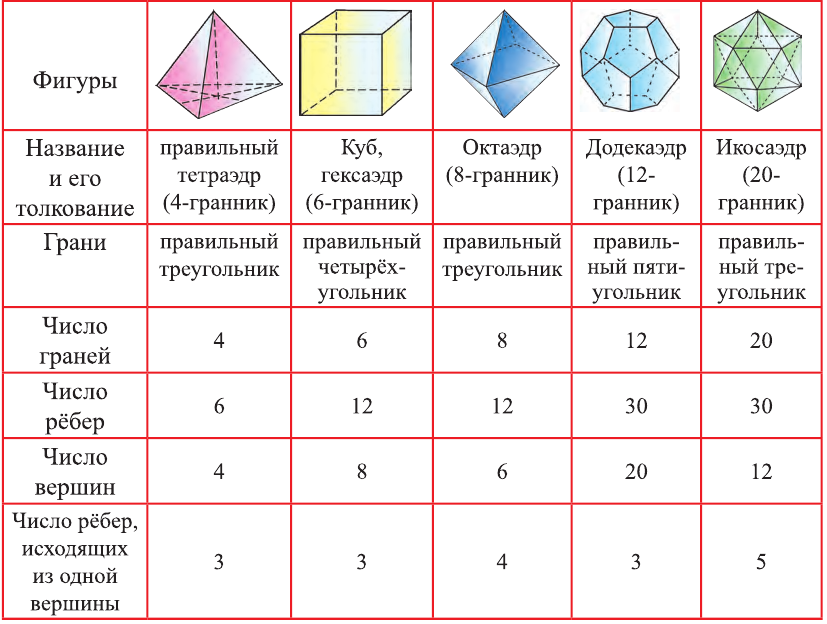

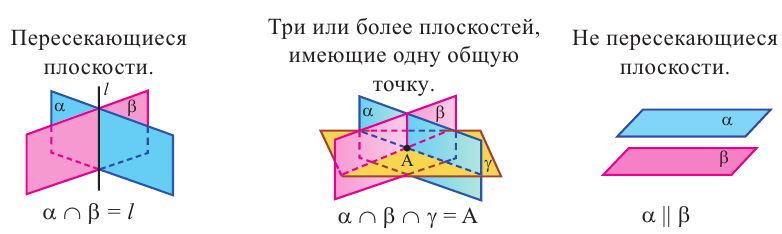
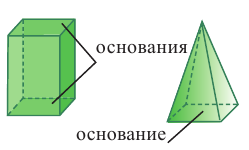
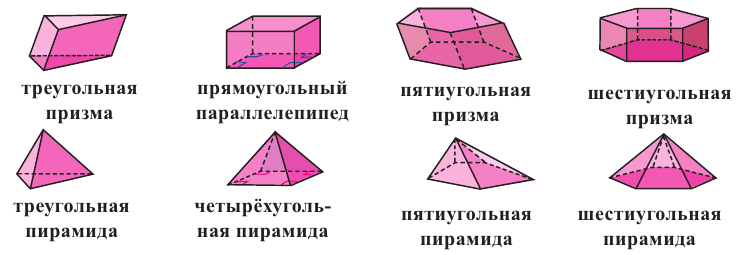

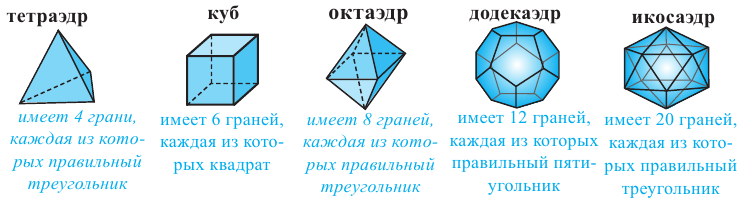
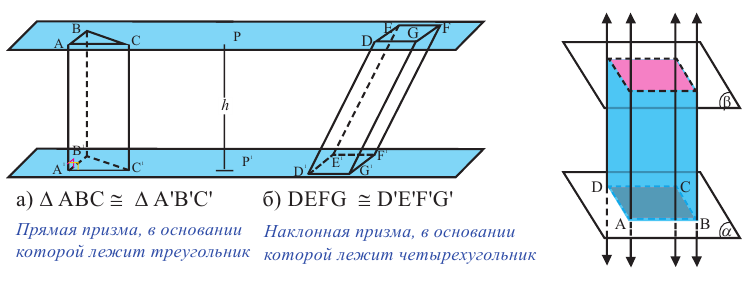
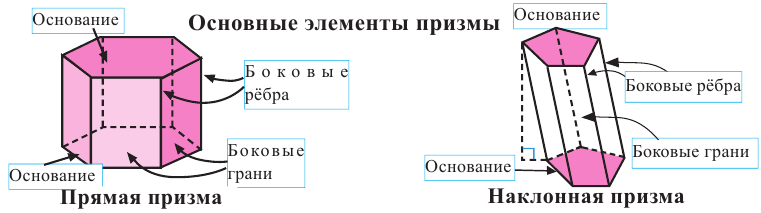
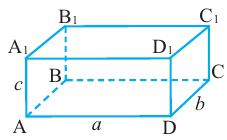
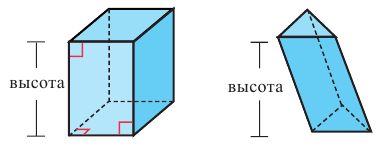
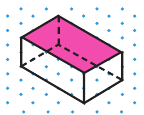
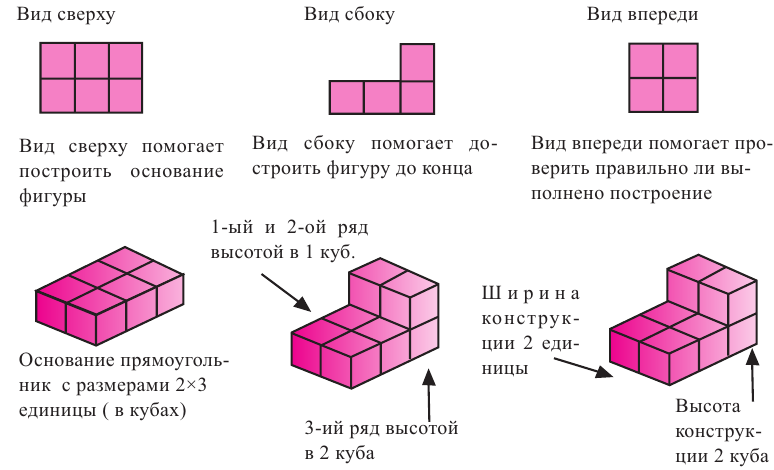
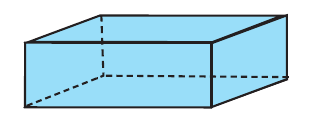
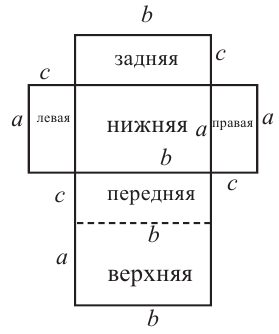
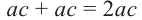
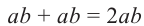
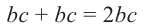
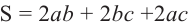
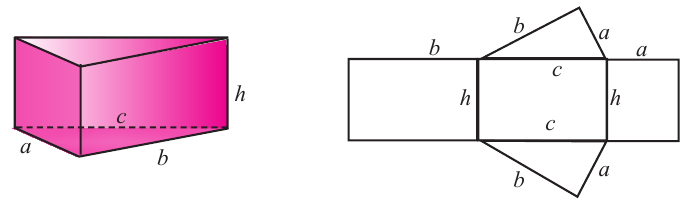
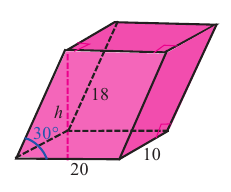
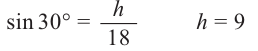
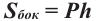
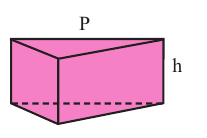
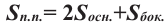

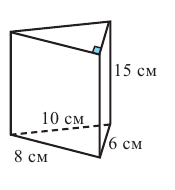
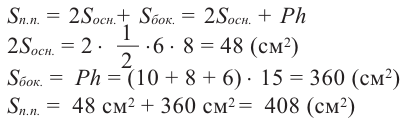
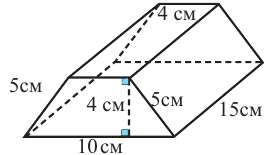
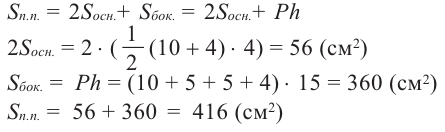
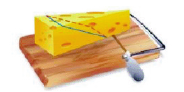
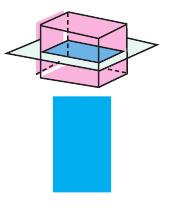
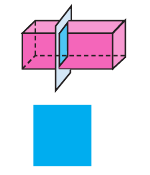
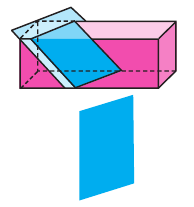
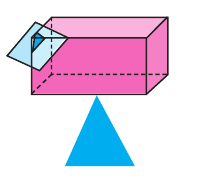
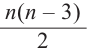
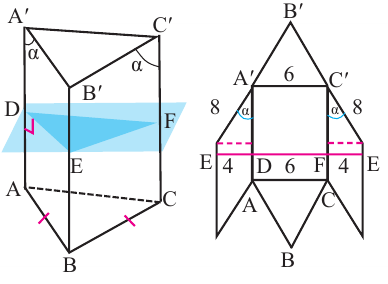
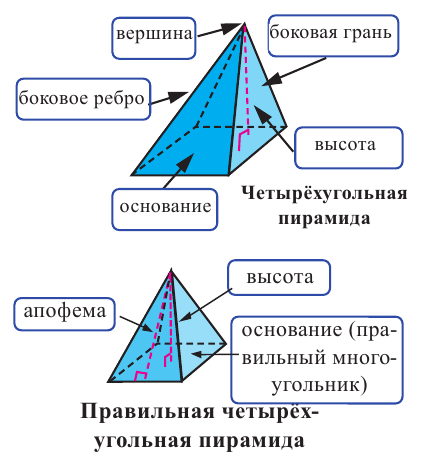
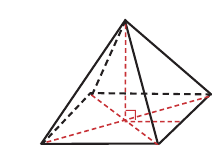
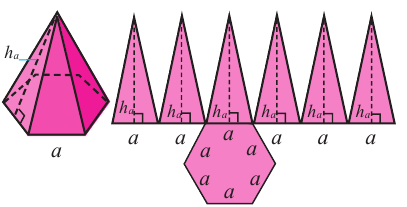
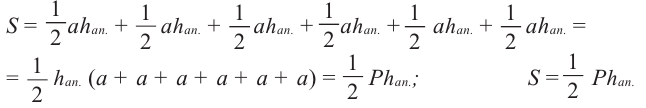
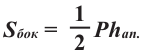
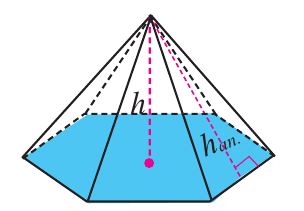
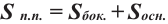
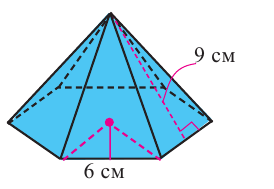
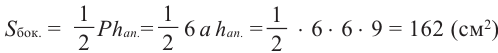
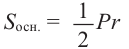
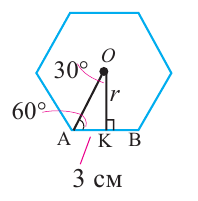
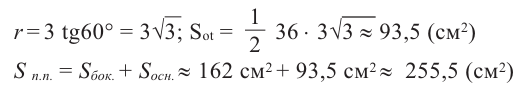
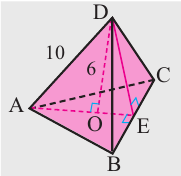
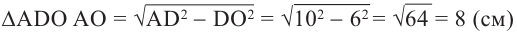
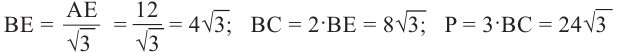
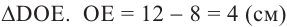
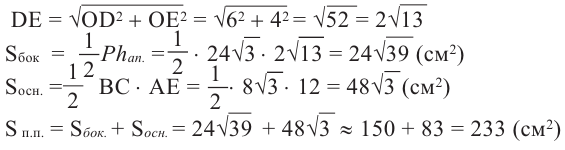
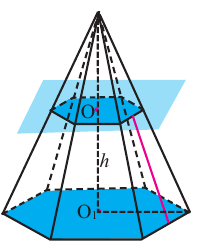
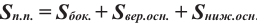
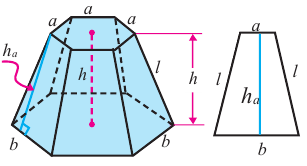
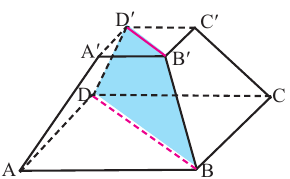
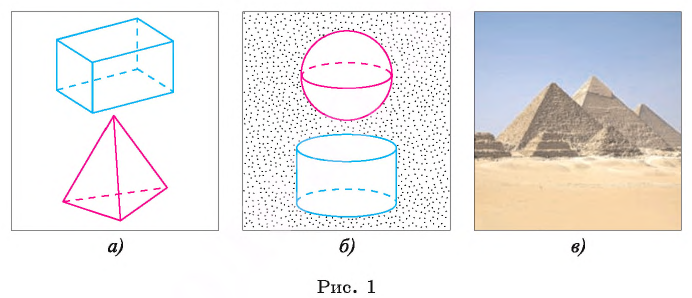
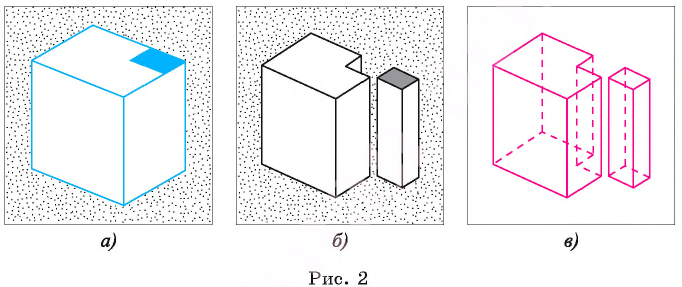
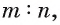 изображается точкой, делящей его изображение в отношении
изображается точкой, делящей его изображение в отношении 
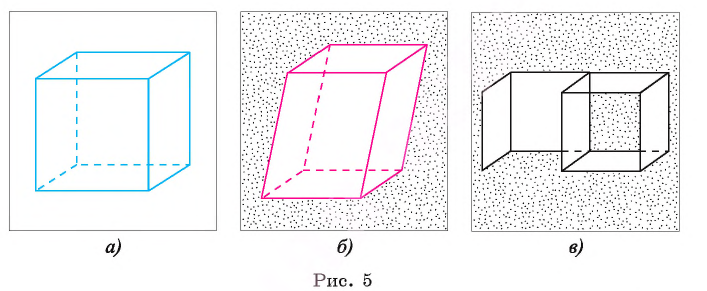
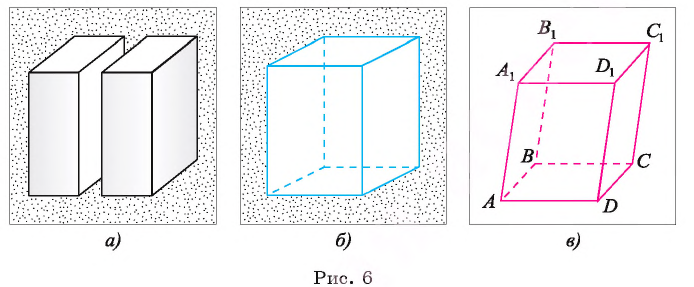
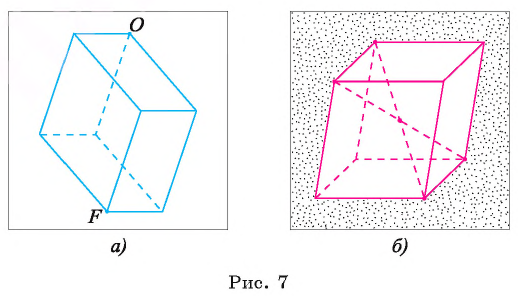
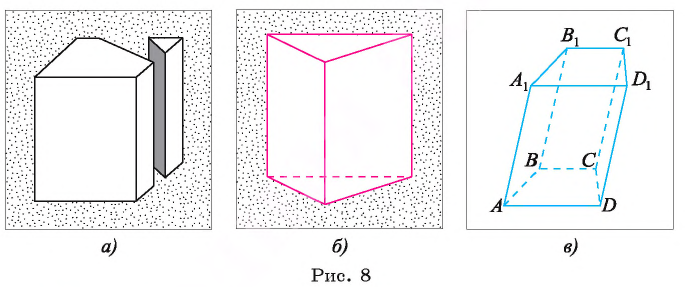
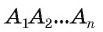
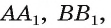
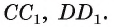
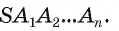
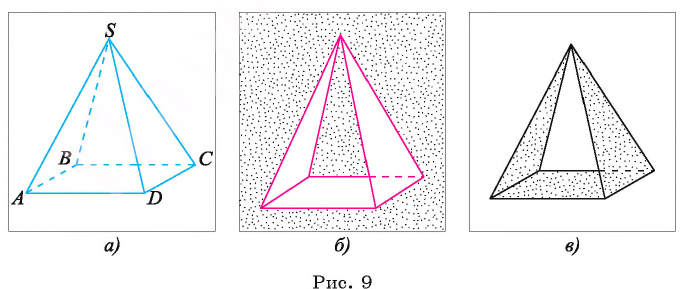
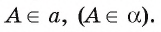
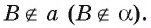
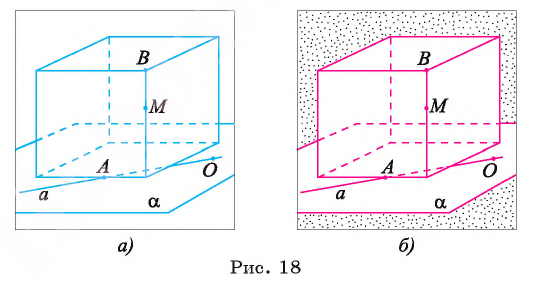
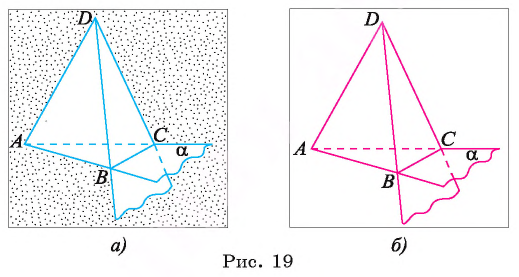
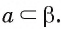
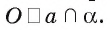
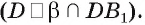
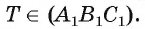

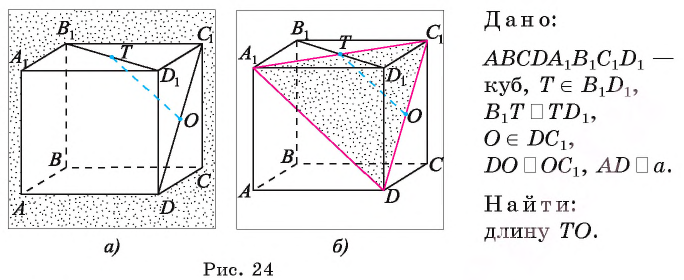
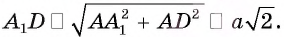
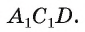
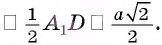
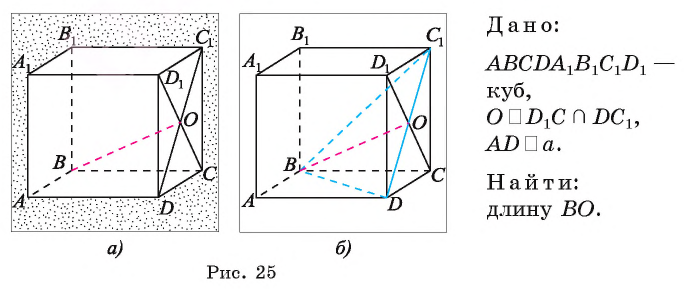
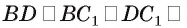
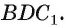
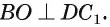

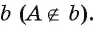
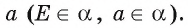

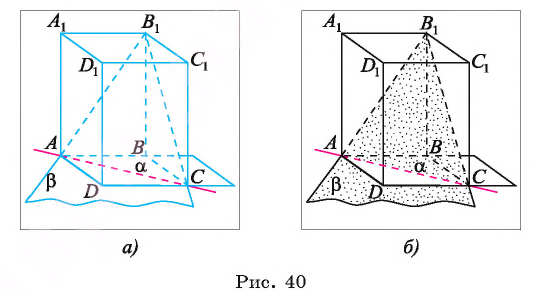
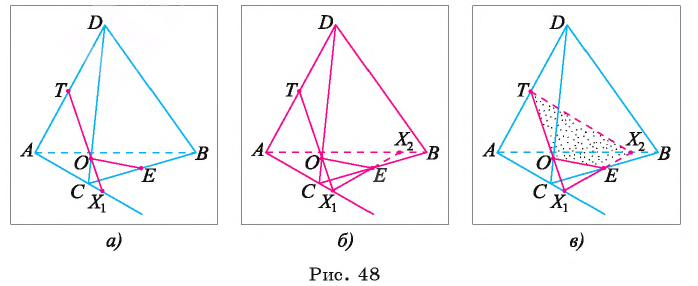
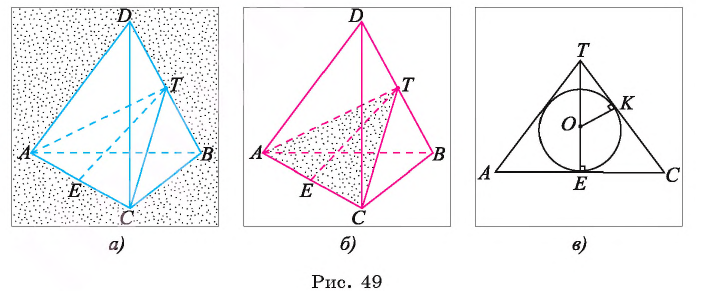
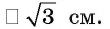
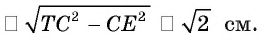
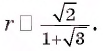
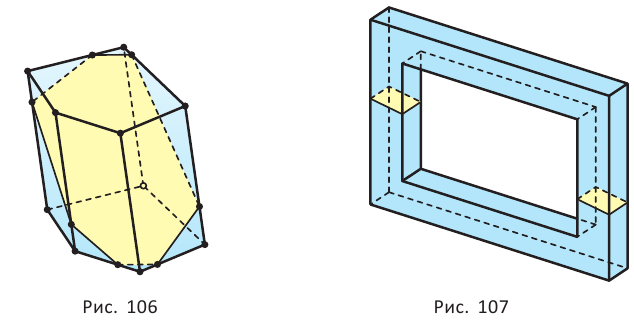
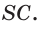
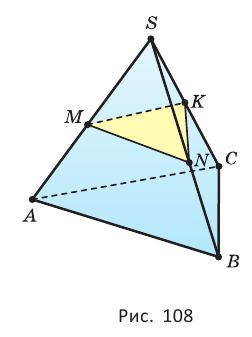
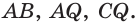
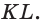
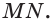
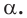
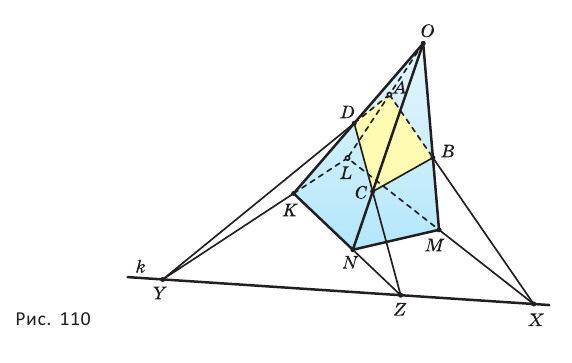
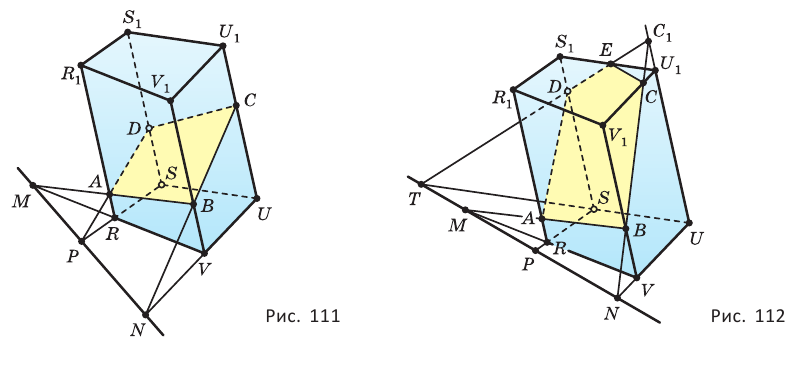
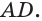
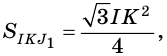
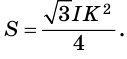
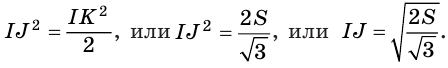
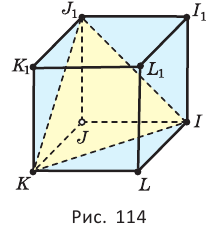
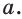
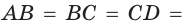
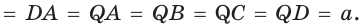
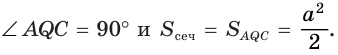
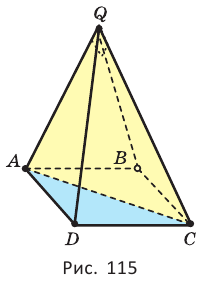

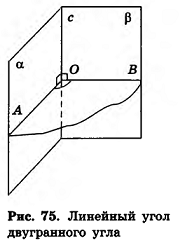
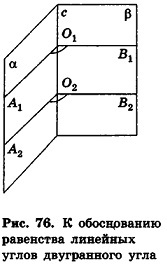
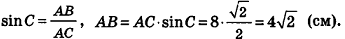
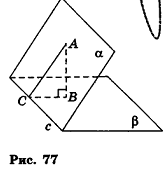
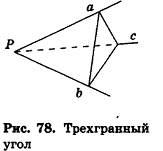
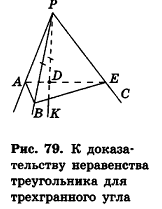
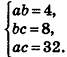
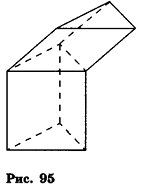

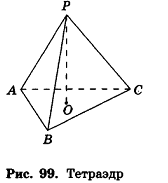

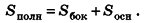
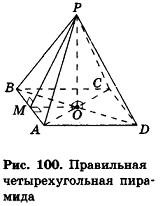
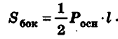
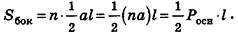
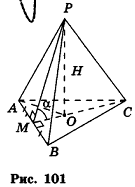
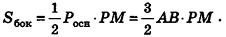
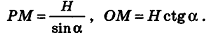
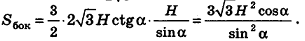
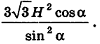
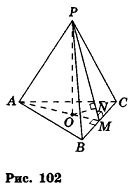
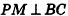 , РМ — апофема данной правильной пирамиды. Так как
, РМ — апофема данной правильной пирамиды. Так как 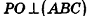 , а отрезок ОМ — проекция наклонной РМ на плоскость ABC, то по теореме о трех перпендикулярах
, а отрезок ОМ — проекция наклонной РМ на плоскость ABC, то по теореме о трех перпендикулярах 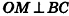 .
.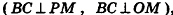 , то по признаку перпендикулярности прямой и плоскости
, то по признаку перпендикулярности прямой и плоскости 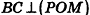 .
.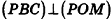 .
.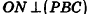 по свойству двух перпендикулярных плоскостей. Значит, отрезок ON — расстояние от точки О до плоскости РВС.
по свойству двух перпендикулярных плоскостей. Значит, отрезок ON — расстояние от точки О до плоскости РВС.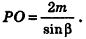
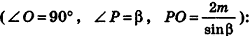
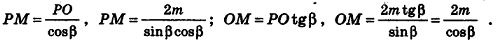
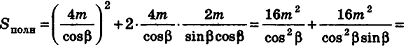
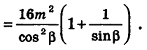
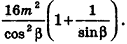
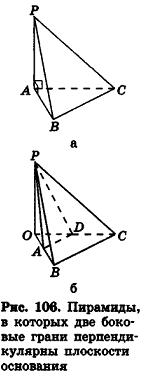
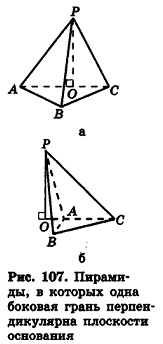
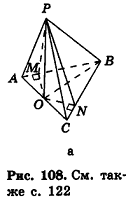
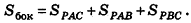
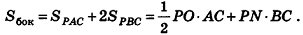
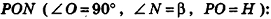
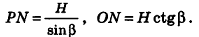
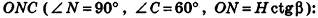
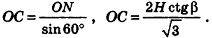
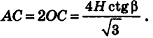
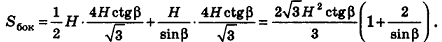
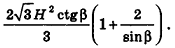
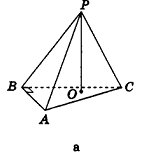
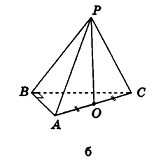
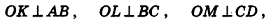
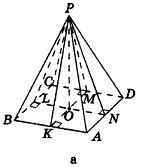
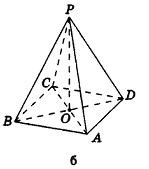
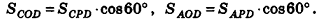
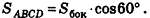
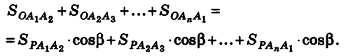
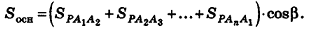
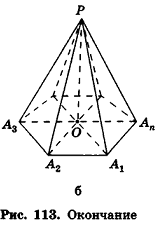
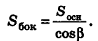
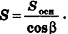
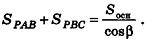
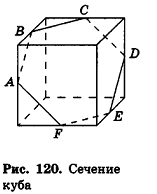
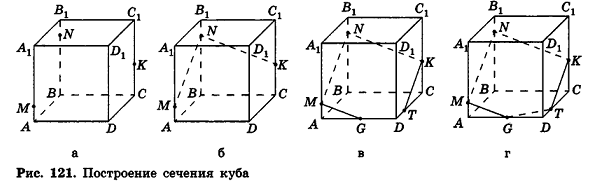
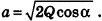
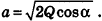
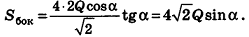
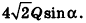
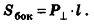
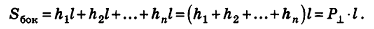
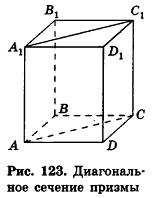
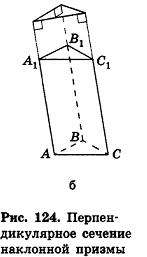
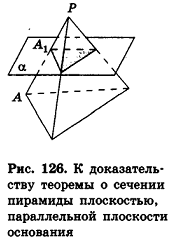
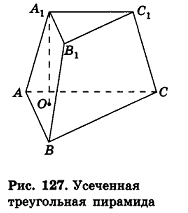
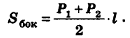
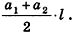
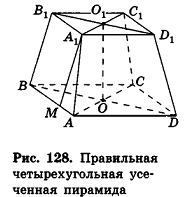
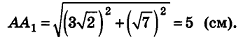
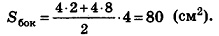
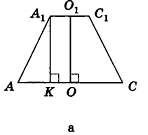
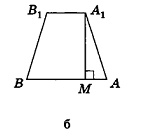
 — высота пирамиды,
— высота пирамиды, — радиусы окружностей, описанных около оснований,
— радиусы окружностей, описанных около оснований,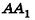 — боковое ребро,
— боковое ребро,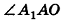 — угол наклона бокового ребра к плоскости большего основания;
— угол наклона бокового ребра к плоскости большего основания; — радиусы окружностей, вписанных в основания,
— радиусы окружностей, вписанных в основания, — высота боковой грани,
— высота боковой грани, — линейный угол двугранного угла при большем основании.
— линейный угол двугранного угла при большем основании.

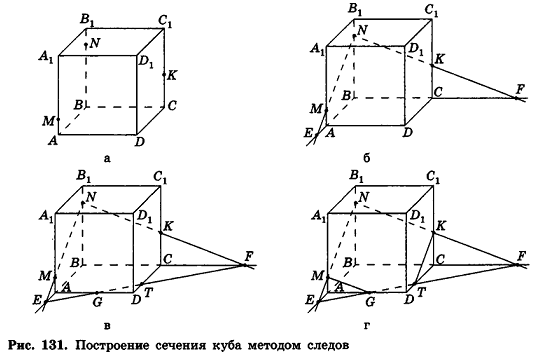
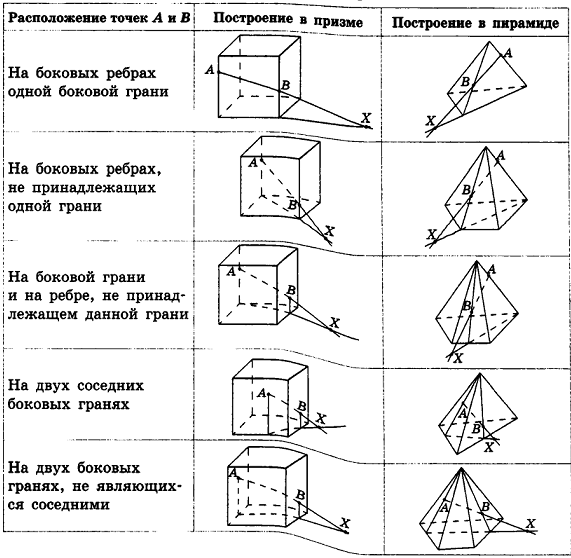
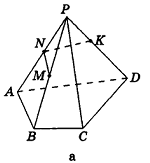
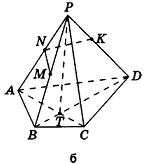
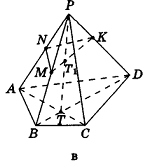
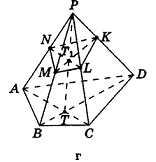


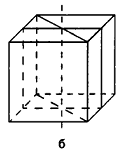

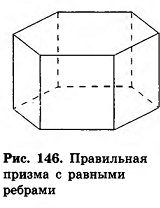
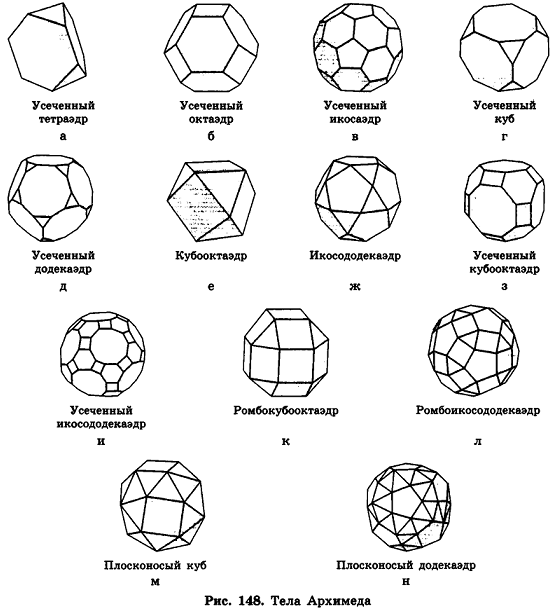




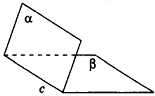
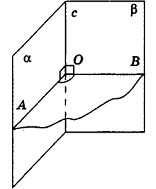
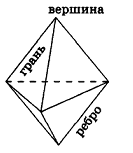
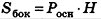
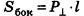
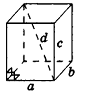
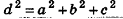
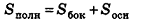
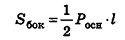
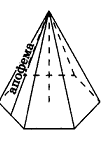
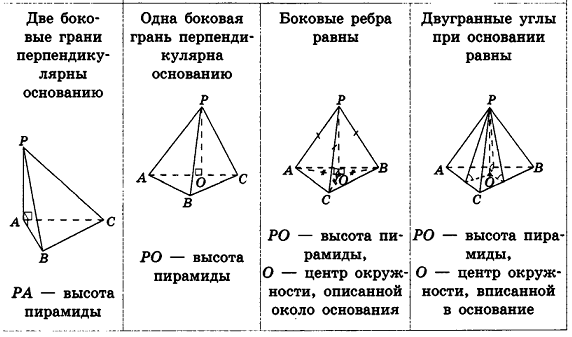
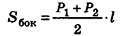
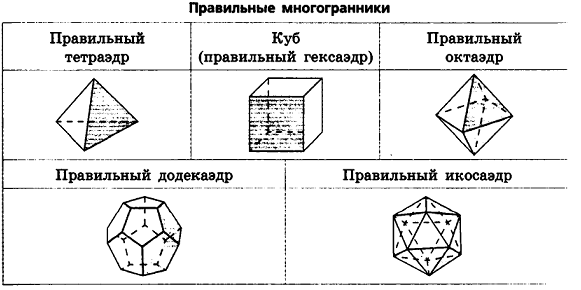




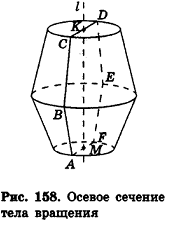





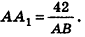
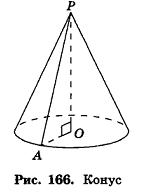

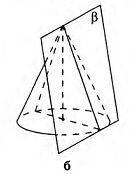

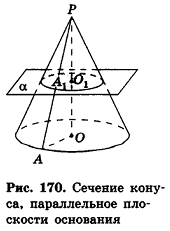
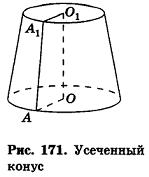
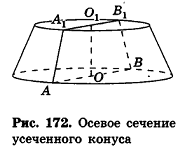
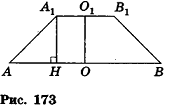
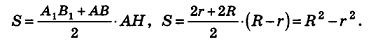
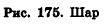
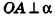 , то для любой точки М плоскости а
, то для любой точки М плоскости а 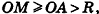 то есть плоскость а не содержит точек шара;
то есть плоскость а не содержит точек шара;