Метод прямоугольников – метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на константу, для каждого элементарного отрезка.
- Описание алгоритма
- Вычисление определённых интегралов: базовые алгоритмы
- Определение интеграла
- Квадратурные формулы
- Вычислительная задача
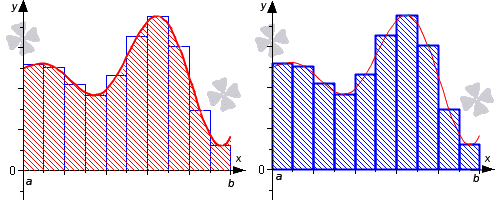
- Кусочно-постоянная аппроксимация
- Кусочно-линейная аппроксимация
- Контроль точности вычисления
- Кусочно-параболическая аппроксимация
- Что дальше?
- Некоторые замечания
- Заключение
- Метод прямоугольников
- Суть метода прямоугольников
- Метод средних прямоугольников
- Оценка абсолютной погрешности метода средних прямоугольников
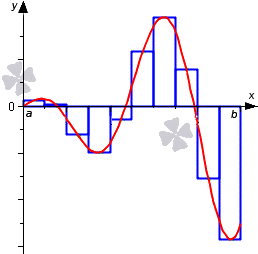
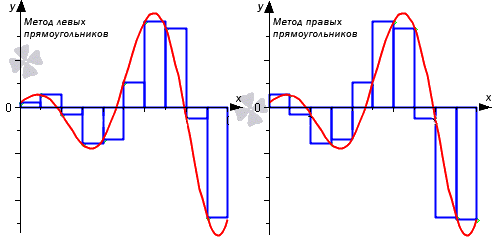
- Метод левых прямоугольников и метод правых прямоугольников
- Примеры применения метода прямоугольников при приближенном вычислении определенных интегралов
- Замечание
- Итоги
- 🌟 Видео
Видео:Метод прямоугольников для нахождения определенного интегралаСкачать

Описание алгоритма
Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах.
Если отрезок [a, b] является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по одной из трех формул:
Формула левых прямоугольников
Формула правых прямоугольников
Формула центральных прямоугольников
Видео:Метод левых, правых и средних прямоугольниковСкачать

Вычисление определённых интегралов: базовые алгоритмы

В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают «под капотом», и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.
Определение интеграла
Интегралом (по Риману) от функции на отрезке
называется следующий предел:
где — мелкость разбиения,
,
,
— произвольное число на отрезке
.
Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким. 
Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).
Квадратурные формулы
Определение интеграла (1) можно переписать в виде
где — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа
точек, в которых вычисляется функция.
Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки и веса
таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.
Вычислительная задача
Задана функция , для которой есть алгоритм вычисления значений в любой точке отрезка
(имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).
Требуется найти приближённое значение интеграла .
Решения будут реализованы на языке Python 3.6.
Для проверки методов используется интеграл .
Кусочно-постоянная аппроксимация
Идейно простейшие квадратурные формулы возникают из применения выражения (1) «в лоб»:
Т.к. от метода разбиения отрезка точками и выбора точек
значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1)
; 2)
; 3)
.
Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.
Для анализа производительности квадратурных формул построим график погрешности в координатах «число точек — отличие численного результата от точного».
Что можно заметить:
- Формула со средней точкой гораздо точнее, чем с правой или левой точками
- Погрешность формулы со средней точкой падает быстрее, чем у двух остальных
- При очень мелком разбиении погрешность формулы со средней точкой начинает возрастать
Первые два пункта связаны с тем, что формула прямоугольников со средней точкой имеет второй порядок аппроксимации, т.е., а формулы правых и левых прямоугольников — первый порядок, т.е.
.
Возрастание погрешности при измельчении шага интегрирования связано с нарастанием погрешности округления при суммировании большого числа слагаемых. Эта ошибка растёт как, что не даёт при интегрировании достигнуть машинной точности.
Вывод: методы прямоугольников с правой и левой точками имеют низкую точность, которая к тому же медленно растёт с измельчением разбиения. Поэтому они имеют смысл разве что в демонстрационных целях. Метод прямоугольников со средней точкой имеет более высокий порядок аппроксимации, что даёт ему шансы на использование в реальных приложениях (об этом чуть ниже).
Кусочно-линейная аппроксимация
Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:

Иллюстрация метода трапеций для n=1 и n=2.
В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид
Построив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).
Контроль точности вычисления
Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.
Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: . Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.
Метод прямоугольников не требует вычислять значения функции на концах отрезка. Это означает, что его можно использовать для функций, имеющих на краях отрезка интегрируемые особенности (например, sinx/x или x -1/2 от 0 до 1). Поэтому показанный далее метод экстраполяции будет работать точно так же и для метода прямоугольников. Отличие от метода трапеций лишь в том, что при уменьшении шага вдвое отбрасывается результат предыдущих вычислений, однако можно утроить число точек, и тогда предыдущее значение интеграла также можно использовать для вычисления нового. Формулы для экстраполяции в этом случае необходимо скорректировать на другое соотношение шагов интегрирования.
Отсюда получаем следующий код для метода трапеций с контролем точности:
С таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.
Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.
Кусочно-параболическая аппроксимация
Следующим шагом аппроксимируем функцию элементами парабол. Для этого требуется, чтобы число отрезков разбиения было чётным, тогда параболы могут быть проведены через тройки точек с абсциссами <(x0=a, x1, x2), (x2, x3, x4), . (xn-2, xn-1, xn=b)>.

Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).
Приближая интеграл от функции на каждом из отрезков [xk;xk+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (xk+1=xk+h), получаем формулу Симпсона:
Из формулы (4) напрямую получается «наивная» реализация метода Симпсона:
Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.
Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам :
Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.
Сравним эффективность метода трапеций и парабол:
Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!
Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).

Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.
Что дальше?
Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов wi в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.
Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:
На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.
Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.
Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.
Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:
Повторяя аналогичную процедуру для формулы Симпсона, получаем:
Если продолжить, вырисовывается такая таблица:
| 2 порядок | 4 порядок | 6 порядок | . |
|---|---|---|---|
| I0,0 | |||
| I1,0 | I1,1 | ||
| I2,0 | I2,1 | I2,2 | |
| . | . | . |
В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).
Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:
Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.
Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.
Дополнительный метод добавляется в класс Quadrature
Проверим, как работает аппроксимация высокого порядка:
Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:
Некоторые замечания
Замечание 1. Количество вызовов функции в этих задачах характеризует число суммирований при вычислении интеграла. Уменьшение числа вычислений подынтегрального выражения не только экономит вычислительные ресурсы (хотя при более оптимизированной реализации и это тоже), но и уменьшает влияние погрешностей округления на результат. Так, при попытке вычислить интеграл тестовой функции метод трапеций зависает при попытке достигнуть относительной точности 5×10 -15 , метод парабол — при желаемой точности 2×10 -16 (что является пределом для чисел в двойной точности), а метод Ромберга справляется с вычислением тестового интеграла вплоть до машинной точности (с ошибкой в младшем бите). То есть, повышается не только точность интегрирования при заданном числе вызовов функции, но и предельно достижимая точность вычисления интеграла.
Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.
Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:
Замечание 4. Может показаться, что чем выше порядок аппроксимации, тем лучше. На самом деле, лучше ограничить число столбцов таблицы Ромберга на уровне 4-6. Чтобы понять это, посмотрим на формулу (6). Второе слагаемое представляет собой разность двух последовательных элементов j-1-го столбца, поделенную на примерно 4 j . Т.к. в j-1-м столбце находятся аппроксимации интеграла порядка 2j, то сама разность имеет порядок (1/ni) 2j
4 —ij . C учётом деления получается
7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.
Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла и эквивалентного ему
. Как говорится, почувствуйте разницу.
Заключение
Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования «обычных» функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.
Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).
Видео:Численное интегрирование: Методы Левых Правых прямоугольников, Трапеций, Симпсона c++Скачать

Метод прямоугольников
Не всегда имеется возможность вычисления интегралов по формуле Ньютона-Лейбница. Не все подынтегральные функции имеют первообразные элементарных функций, поэтому нахождение точного числа становится нереальным. При решении таких задач не всегда необходимо получать на выходе точные ответы. Существует понятие приближенного значения интеграла, которое задается методом числового интегрирования типа метода прямоугольников, трапеций, Симпсона и другие.
Данная статья посвящена именно этому разделу с получением приближенных значений.
Будет определена суть метода Симпсона, получим формулу прямоугольников и оценки абсолютной погрешности, метод правых и левых треугольников. На заключительном этапе закрепим знания при помощи решения задач с подробным объяснением.
Видео:Метод средних прямоугольниковСкачать

Суть метода прямоугольников
Если функция y = f ( x ) имеет непрерывность на отрезке [ a ; b ] и необходимо вычислить значение интеграла ∫ a b f ( x ) d x .
Необходимо воспользоваться понятием неопределенного интеграла. Тогда следует разбить отрезок [ a ; b ] на количество n частей x i — 1 ; x i , i = 1 , 2 , . . . . , n , где a = x 0 x 1 x 2 . . . x n — 1 x n = b . В промежутке отрезка x i — 1 ; x i , i = 1 , 2 , . . . , n выберем точку со значением ζ i . Из определения имеем, что существует определенный тип интегральных сумм при бесконечном уменьшении длины элементарного отрезка, который уже разбили. Это выражается формулой λ = m a x i = 1 , 2 , . . . , n ( x i — x i — 1 ) → 0 , тогда получаем, что любая из таких интегральных сумм – приближенное значение интеграла ∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( ζ i ) · ( x i — x i — 1 ) .
Суть метода прямоугольников выражается в том, что приближенное значение считается интегральной суммой.
Видео:Метод левых и метод правых прямоугольниковСкачать

Метод средних прямоугольников
Если разбить интегрируемый отрезок [ a ; b ] на одинаковые части точкой h , то получим a = x 0 , x 1 = x 0 + h , x 2 = x 0 + 2 h , . . . , x — 1 = x 0 + ( n — 1 ) h , x n = x 0 + n h = b , то есть h = x i — x i — 1 = b — a n , i = 1 , 2 , . . . , n . Серединами точек ζ i выбираются элементарные отрезки x i — 1 ; x i , i = 1 , 2 , . . . , n , значит ζ i = x i — 1 + h 2 , i = 1 , 2 , . . . , n .
Тогда приближенное значение ∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( ζ i ) · ( x i — x i — 1 ) записывается таким образом ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( ζ i ) x i — 1 + h 2 . Данная формула называется формулой метода прямоугольников.
Такое название метод получает из-за характера выбора точек ζ i , где шаг разбиения отрезка берется за h = b — a n .
Рассмотрим на приведенном ниже рисунке данный метод.
Чертеж явно показывает, что приближение к кусочной ступенчатой функции
y = f x 0 + h 2 , x ∈ [ x 0 ; x 1 ) f x 1 + h 2 , x ∈ [ x 1 ; x 2 ) . . . f x n — 1 + h 2 , x ∈ [ x n — 1 ; x n ] происходит на всем пределе интегрирования.
С геометрической стороны мы имеем, что неотрицательная функция y = f ( x ) на имеющемся отрезке [ a ; b ] имеет точное значение определенного интеграла и выглядит как криволинейная трапеция, площадь которой необходимо найти. Рассмотрим на рисунке, приведенном ниже.
Видео:3.2 Численное интегрирование (лекция)Скачать
Оценка абсолютной погрешности метода средних прямоугольников
Для оценки абсолютной погрешности необходимо выполнить ее оценку на заданном интервале. То есть следует найти сумму абсолютных погрешностей каждого интервала. Каждый отрезок x i — 1 ; x i , i = 1 , 2 , . . . , n имеет приближенное равенство ∫ x i — 1 x i f ( x ) d x ≈ f x i — 1 + h 2 · h = f x i — 1 + h 2 · ( x i — x i — 1 ) . Абсолютная погрешность данного метода треугольников δ i , принадлежащей отрезку i , вычисляется как разность точного и приближенного определения интеграла . Имеем, что δ i = ∫ x i — 1 x i f ( x ) d x — f x i — 1 + h 2 · x i — x i — 1 . Получаем, что f x i — 1 + h 2 является некоторым числом, а x i — x i — 1 = ∫ x i — 1 x i d x , тогда выражение f x i — 1 + h 2 · x i — x i — 1 по 4 свойству определения интегралов записывается в форме f x i — 1 + h 2 · x i — x i — 1 = ∫ x — 1 x f x i — 1 + h 2 d x . Отсюда получаем, что отрезок i имеет абсолютную погрешность вида
δ i = ∫ x i — 1 x i f ( x ) d x — f x i — 1 + h 2 · x i — x i — 1 = = ∫ x i — 1 x i f ( x ) d x — ∫ x i — 1 x i x i — 1 + h 2 d x = ∫ x i — 1 x i f ( x ) = — f x i — 1 + h 2 d x
Если взять, что функция y = f ( x ) имеет производные второго порядка в точке x i — 1 + h 2 и ее окрестностях, тогда y = f ( x ) раскладывается в ряд Тейлора по степеням x — x i — 1 + h 2 с остаточным членом в форме разложения по Лагранжу. Получаем, что
f ( x ) = f x i — 1 + h 2 + f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 + + f » ( ε i ) x — x i — 1 + h 2 2 2 ⇔ ⇔ f ( x ) = f ( x i — 1 + h 2 ) = f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 + + f » ( ε i ) x — x i — 1 + h 2 2 2
Исходя из свойства определенного интеграла, равенство может интегрироваться почленно. Тогда получим, что
∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x = ∫ x i — 1 x i f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 d x + + ∫ x i — 1 x i f » ε i · x — x i — 1 + h 2 2 2 d x = = f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 2 2 x i — 1 x i + f » ε i · x — x i — 1 + h 2 3 6 x i — 1 x i = = f ‘ x i — 1 + h 2 · x i — h 2 2 2 — x i — 1 — x i — 1 + h 2 2 2 + + f » ε i · x i — h 2 3 6 — x i — 1 — x i — 1 + h 2 3 6 = = f ‘ x i — 1 + h 2 · h 2 8 — h 2 8 + f » ( ε i ) · h 3 48 + h 3 48 = f » ε i · h 3 24
где имеем ε i ∈ x i — 1 ; x i .
Отсюда получаем, что δ i = ∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x = f » ε i · h 3 24 .
Абсолютная погрешность формулы прямоугольников отрезка [ a ; b ] равняется сумме погрешностей каждого элементарного интервала. Имеем, что
δ n = ∑ i = 1 n ∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x и δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) · n · h 3 24 = m a x x ∈ [ a ; b ] f » ( x ) = b — a 3 24 n 2 .
Неравенство является оценкой абсолютной погрешности метода прямоугольников.
Видео:3. Численные методы расчета определенного интеграла: прямоугольников, трапеции, парабол (Симпсона)Скачать
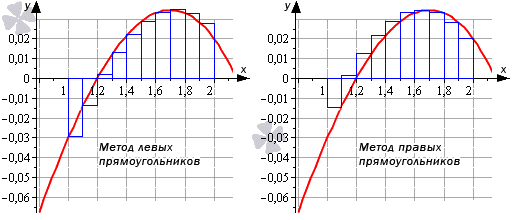
Метод левых прямоугольников и метод правых прямоугольников
Для модификации метода рассмотрим формулы.
∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) является формулой левых треугольников.
∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) является формулой правых треугольников.
Рассмотрим на примере рисунка, приведенного ниже.
Отличием метода средних прямоугольников считается выбор точек не по центру, а на левой и правой границах данных элементарных отрезков.
Такая абсолютная погрешность методов левых и правых треугольников можно записать в виде
δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · h 2 · n 2 = m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n
Видео:метод прямоугольниковСкачать
Примеры применения метода прямоугольников при приближенном вычислении определенных интегралов
Необходимо рассмотреть решение примеров, где нужно вычислять примерное значение имеющегося определенного интеграла при помощи метода прямоугольников. Рассматривают два типа решения заданий. Суть первого случая – задание количества интервалов для разбивания отрезка интегрирования. Суть второго заключается в наличии допустимой абсолютной погрешности.
Формулировки задач выглядят следующим образом:
- произвести приближенное вычисление определенного интеграла при помощи метода прямоугольников, разбивая на nколичество отрезков интегрирования;
- найти приближенное значение определенного интеграла методом прямоугольников с точностью до одной сотой.
Рассмотрим решения в обоих случаях.
В качестве примера выбрали задания, которые поддаются преобразованию для нахождения их первообразных. Тогда появляется возможность вычисления точного значения определенного интеграла и сравнения с приближенным значением при помощи метода прямоугольников.
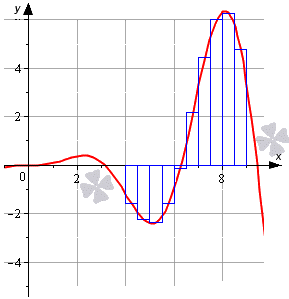
Произвести вычисление определенного интеграла ∫ 4 9 x 2 sin x 10 d x при помощи метода прямоугольников, разбивая отрезок интегрирования на 10 частей.
Из условия имеем, что a = 4 , b = 9 , n = 10 , f ( x ) = x 2 sin x 10 . Для применения ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f x i — 1 + h 2 необходимо вычислить размерность шага h и значение функции f ( x ) = x 2 sin x 10 в точках x i — 1 + h 2 , i = 1 , 2 , . . . , 10 .
Вычисляем значение шага и получаем, что
h = b — a n = 9 — 4 10 = 0 . 5 .
Потому как x i — 1 = a + ( i — 1 ) · h , i = 1 , . . . , 10 , тогда x i — 1 + h 2 = a + ( i — 1 ) · h + h 2 = a + i — 0 . 5 · h , i = 1 , . . . , 10 .
Так как i = 1 , то получаем x i — 1 + h 2 = x 0 + h 2 = a + ( i — 0 . 5 ) · h = 4 + ( 1 — 0 . 5 ) · 0 . 5 = 4 . 25 .
После чего необходимо найти значение функции
f x i — 1 + h 2 = f x 0 + h 2 = f ( 4 . 25 ) = 4 . 25 2 sin ( 4 . 25 ) 10 ≈ — 1 . 616574
При i = 2 получаем x i — 1 + h 2 = x 1 + h 2 = a + i — 0 . 5 · h = 4 + ( 2 — 0 . 5 ) · 0 . 5 = 4 . 75 .
Нахождение соответствующего значения функции получает вид
f x i — 1 + h 2 = f x 1 + h 2 = f ( 4 . 75 ) = 4 . 75 2 sin ( 4 . 75 ) 10 ≈ — 2 . 254654
Вычисления производятся до i = 10 .
Представим эти данные в таблице, приведенной ниже.
| i | 1 | 2 | 3 | 4 | 5 |
| x i — 1 + h 2 | 4 . 25 | 4 . 75 | 5 . 25 | 5 . 75 | 6 . 25 |
| f x i — 1 + h 2 | — 1 . 616574 | — 2 . 254654 | — 2 . 367438 | — 1 . 680497 | — 0 . 129606 |
| i | 6 | 7 | 8 | 9 | 10 |
| x i — 1 + h 2 | 6 . 75 | 7 . 25 | 7 . 75 | 8 . 25 | 8 . 75 |
| f x i — 1 + h 2 | 2 . 050513 | 4 . 326318 | 5 . 973808 | 6 . 279474 | 4 . 783042 |
Значения функции необходимо подставить в формулу прямоугольников. Тогда получаем, что
∫ 4 9 x 2 sin x 10 d x ≈ h · ∑ i = 1 n f x i — 1 + h 2 = = 0 . 5 · — 1 . 616574 — 2 . 25654 — 2 . 367438 — 1 . 680497 — 0 . 129606 + + 2 . 050513 + 4 . 326318 + 5 . 973808 + 6 . 279474 + 4 . 783042 = = 7 . 682193
Исходный интеграл можно вычислить при помощи формулы Ньютона-Лейбница. Получаем, что
∫ 4 9 x 2 · sin x 10 d x = — 1 10 x 2 · cos x + 1 5 x · sin x + 1 5 cos x 4 9 = = 7 5 cos 4 — 4 5 sin 4 — 79 10 cos 9 + 9 5 sin 9 ≈ 7 . 630083
Находим первообразную выражения — 1 10 x 2 · cos x + 1 5 x · sin x + 1 5 cos x соответствующую функции f ( x ) = x 2 sin x 10 . Нахождение производится методом интегрирования по частям.
Отсюда видно, что определенный интеграл отличается от значения, полученном при решении методом прямоугольников, где n = 10 , на 6 долей единицы. Рассмотрим на рисунке, приведенном ниже.
Вычислить приближенного значение определенного интеграла ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x при помощи метода левых и правых прямоугольников с точностью до одной сотой.
Из условия мы имеем, что a = 1 , b = 2 и f ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 .
Для применения формулы правых и левых прямоугольников нужно знать размерность шага h , а для его вычисления разбиваем отрезок интегрирования на n отрезков. По условию имеем, что точность должна быть до 0 , 01 , тогда нахождение n возможно при помощи оценки абсолютной погрешности методов левых и правых прямоугольников.
Известно, что δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n . Для достижения необходимой степени точности необходимо найти такое значение n , для которого неравенство m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n ≤ 0 . 01 будет выполнено.
Найдем наибольшее значение модуля первой производной, то есть значение m a x x ∈ [ a ; b ] f ‘ ( x ) подынтегральной функции f ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 , определенной на отрезке [ 1 ; 2 ] . В нашем случае необходимо выполнить вычисления:
f ‘ ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ‘ = — 0 . 09 x 2 + 0 . 26
Парабола является графиком подынтегральной функции с ветвями, направленными вниз, определенная на отрезке [ 1 ; 2 ] , причем с монотонно убывающим графиком. Необходимо произвести вычисление модулей значений производных на концах отрезков, а из них выбрать наибольшее значение. Получаем, что
f ‘ ( 1 ) = — 0 . 09 · 1 2 + 0 . 26 = 0 . 17 f ‘ ( 2 ) = — 0 . 09 · 2 2 + 0 . 26 = 0 . 1 → m a x x ∈ [ 1 ; 2 ] f ‘ ( x ) = 0 . 17
Решение сложных подынтегральных функций подразумевает обращение к разделу наибольше и наименьшее значение функции.
Тогда получаем, что наибольшее значение функции имеет вид:
m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n ≤ 0 . 01 ⇔ ⇔ 0 . 17 · ( 2 — 1 ) 2 2 n ≤ 0 . 01 ⇔ 0 . 085 n ≤ 0 . 01 ⇔ n ≥ 8 . 5
Дробность числа n исключается, так как n является натуральным числом. Чтобы прийти к точности 0 . 01 , используя метод правых и левых прямоугольников, не обходимо выбирать любое значение n . Для четкости расчетов возьмем n = 10 .
Тогда формула левых прямоугольников примет вид ∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) , а правых — ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) . Для применения их на практике необходимо найти значение размерности шага h и f ( x i ) , i = 0 , 1 , . . . , n , где n = 10 .
h = b — a n = 2 — 1 10 = 0 . 1
Определение точек отрезка [ a ; b ] производится с помощью x i = a + i · h , i = 0 , 1 , . . . , n .
При i = 0 , получаем x i = x 0 = a + i · h = 1 + 0 · 0 . 1 = 1 и f ( x i ) = f ( x 0 ) = f ( 1 ) = — 0 . 03 · 1 3 + 0 . 26 · 1 — 0 . 26 = — 0 . 03 .
При i = 1 , получаем x i = x 1 = a + i · h = 1 + 1 · 0 . 1 = 1 . 1 и f ( x i ) = f ( x 1 ) = f ( 1 . 1 ) = — 0 . 03 · ( 1 . 1 ) 3 + 0 . 26 · ( 1 . 1 ) — 0 . 26 = — 0 . 01393 .
Вычисления производятся до i = 10 .
Вычисления необходимо представить в таблице, приведенной ниже.
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| x i | 1 | 1 . 1 | 1 . 2 | 1 . 3 | 1 . 4 | 1 . 5 |
| f ( x i ) | — 0 . 03 | — 0 . 01393 | 0 . 00016 | 0 . 01209 | 0 . 02168 | 0 . 02875 |
| i | 6 | 7 | 8 | 9 | 10 |
| x i | 1 . 6 | 1 . 7 | 1 . 8 | 1 . 9 | 2 |
| f ( x i ) | 0 . 03312 | 0 . 03461 | 0 . 03304 | 0 . 02823 | 0 . 02 |
Подставим формулу левых треугольников
∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) = = 0 . 1 · — 0 . 03 — 0 . 01393 + 0 . 00016 + 0 . 01209 + 0 . 02168 + + 0 . 02875 + 0 . 03312 + 0 . 03461 + 0 . 03304 + 0 . 02823 = = 0 . 014775
Подставляем в формулу правых треугольников
∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ h · ∑ i = 1 n f ( x i ) = = 0 . 1 · — 0 . 01393 + 0 . 00016 + 0 . 01209 + 0 . 02168 + 0 . 02875 + + 0 . 03312 + 0 . 03461 + 0 . 03304 + 0 . 02823 + 0 . 02 = 0 . 019775
Произведем вычисление по формуле Ньютона-Лейбница:
∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x = = — 0 . 03 x 4 4 + 0 . 13 x 2 — 0 . 26 x 1 2 = 0 . 0175
Рассмотрим рисунок, приведенный ниже.
Видео:Метод левых прямоугольников, разбор задачиСкачать

Замечание
Нахождение наибольшего значения модуля первой производной является трудоемкой работой, поэтому можно исключить использование неравенства для оценивания абсолютной погрешности и методов численного интегрирования. Разрешено применять схему.
Берем значение n = 5 для вычисления приближенного значения интеграла. Необходимо удвоить количество отрезков интегрирования, тогда n = 10 , после чего производится вычисление примерного значения. необходимо найти разность этих значений при n = 5 и n = 10 . Когда разность не соответствует требуемой точности, то приближенным значением считается n = 10 с округлением до десятка.
Когда погрешность превышает необходимую точность, то производится удваивание n и сравнивание приближенных значений. Вычисления производятся до тех пор, пока необходимая точность не будет достигнута.
Для средних прямоугольников выполняются аналогичные действия, но вычисления на каждом шаге требуют разности полученных приближенных значений интеграла для n и 2 n . Такой способ вычисления называется правилом Рунге.
Произведем вычисление интегралов с точностью до одной тысячной при помощи метода левых прямоугольников.
При n = 5 получаем, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 0116 , а при n = 10 — ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 014775 . Так как имеем, что 0 . 0116 — 0 . 014775 = 0 . 003175 > 0 . 001 , возьмем n = 20 . Получаем, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 01619375 . Имеем 0 . 014775 — 0 . 01619375 = 0 . 00141875 > 0 . 001 , возьмем значение n = 40 , тогда получим ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 01686093 . Имеем, что 0 . 1619375 — 0 . 01686093 = 0 . 00066718 0 . 001 , тогда после округления значения проверим, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x равняется значению 0 , 017 с погрешностью 0 , 001 . Из оценок абсолютных погрешностей видно, что данный метод дает максимальную точность в отличие от метода левых и правых координат для заданного n . Отдается предпочтение методу средних прямоугольников.
Непрерывные подынтегральные функции при бесконечном разделении на отрезки данное приближенно число стремится к точному. Чаще всего такой метод выполняется при помощи специальных программ на компьютере. Поэтому чем больше значение n , тем больше вычислительная погрешность.
Для наиболее точного вычисления необходимо выполнять точные промежуточные действия, желательно с точностью до 0 , 0001 .
Видео:Метод трапеций при вычислении определенного интегралаСкачать

Итоги
Для вычисления неопределенного интеграла методом прямоугольников следует применять формулу такого вида ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( ζ i ) x i — 1 + h 2 и оценивается абсолютная погрешность с помощью δ n ≤ m a x x ∈ [ a ; b ] f ‘ ‘ ( x ) · n · h 3 24 = m a x x ∈ [ a ; b ] f ‘ ‘ ( x ) · b — a 3 24 n 2 .
Для решения с помощью методов правых и левых прямоугольников применяют формулы, имеющие вид, ∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) и ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) . Абсолютная погрешность оценивается при помощи формулы вида δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · h 2 · n 2 = m a x x ∈ [ a ; b ] f ‘ ( x ) · b — a 2 2 n .
🌟 Видео
ВАЖНО! Вот ТРИ запаха рака, на которые люди не обращают внимание! Чем пахнет рак (онкология)?Скачать

Математика это не ИсламСкачать

Путешествуя вглубь космического пространстваСкачать

Формула СимпсонаСкачать
Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

Метод трапецийСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Уважение к мужчине / Любовницы / Цена отсутствия уважения — Юлия Ивлиева | Шоу МЕТОД #5Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать