Метод хаоса треугольник серпинского (8 видео)

Игра в хаос и треугольник Серпинского на C#

Игра «Хаос» — это метод создания фрактальных изображений путем построения случайных точек внутри многоугольника в соответствии с простым набором правил. В этой статье мы будем использовать игру в хаос для создания треугольника Серпинского с использованием C# и Windows Forms.

Игра в хаос — это математический термин для метода генерации фрактальных изображений. Игра предоставляет простой набор правил, которые могут создавать удивительно сложные фигуры. Алгоритм задает начальное условие с набором определенных точек, или аттракторов. Множество аттракторов можно рассматривать как ряд вершин многоугольника. Начальная точка в пределах полигона выбирается и наносится на изображение.

Как только начальное условие известно, для создания фрактала выполняется повторяющийся процесс. Сначала выбирается случайная вершина в многоугольнике. Затем текущее положение или начальное положение для первой итерации соединяется с положением аттрактора воображаемой прямой линией. Текущее положение перемещается вдоль этой линии на долю расстояния между двумя точками, и на рисунке отображается новое положение.

Треугольник Серпинского — это фрактал, который был впервые описан польским математиком Вацлавом Серпинским. При отображении он выглядит как треугольник, разделенный на четыре секции, каждая из которых составляет половину высоты и ширины оригинала. Центральный треугольник перевернут и может рассматриваться как отверстие на изображении. Каждый из трех внешних треугольников представляет собой уменьшенную версию всей фигуры с собственным центральным отверстием. Этот шаблон повторяется бесконечно, чтобы получить результат, аналогичный показанному на рисунке ниже:

Треугольник Серпинского

Существуют различные методы, с помощью которых можно создать треугольник Серпинского. Одним из них является использование игры хаоса с тремя аттракторами, расположенными в трех вершинах равностороннего треугольника. При перемещении текущей позиции к аттрактору перемещаемая величина всегда равна половине расстояния между текущей точкой и выбранной вершиной. Таким образом, шаги по созданию фрактала заключаются в следующем:

Определите три точки.
Выберите начальную позицию.
Случайным образом выберите один из трех аттракторов.
Переместите текущее положение на полпути к выбранному положению аттрактора и постройте точку.
Вернитесь к шагу 3.

Рисование треугольника Серпинского

В оставшейся части этой статьи мы создадим программу на C# для создания треугольника Серпинского. Программа, которую мы разработаем, — это та, которая использовалась для создания изображения выше.

Для начала создайте проект Windows Forms. Мы будем использовать форму по умолчанию для отображения треугольника, рисуя непосредственно на поверхности формы. Откройте форму по умолчанию и измените ее свойство BackColor на белый. Мы запустим процесс генерации фрактала в ответ на нажатие кнопки, поэтому добавьте кнопку в форму и нанесите на нее подходящую метку, используя свойство Text.

Переменные области действия на уровне класса

Во время создания изображения есть три элемента, которые будут использоваться различными методами. Первый — генератор псевдослучайных чисел, который будет использоваться для определения направления движения во время каждой итерации игры в хаос. Во-вторых, нам нужно удерживать позиции трех вершин равностороннего треугольника. Мы можем хранить их в небольшом массиве точечных структур. Наконец, еще одна точечная структура сохранит текущую позицию.

Чтобы объявить переменные для этих элементов, добавьте в класс следующие переменные области действия на уровне класса:

Определение размера треугольника

Размер треугольника должен быть как можно больше, чтобы можно было отобразить максимальную детализацию. Тем не менее, мы хотим убедиться, что треугольник является равносторонним и расположен в центре клиентской области формы. Чтобы определить максимально возможный размер, мы должны рассмотреть соотношение между высотой и шириной любого равностороннего треугольника. Предполагая, что основание треугольника выровнено по горизонтали, ширина будет такой же, как длина одной из сторон. Высота будет равна ширине, умноженной на половину квадратного корня из трех.

Мы можем добавить метод в форму для расчета коэффициента, добавив следующий код:

С помощью легко доступного соотношения мы можем определить максимальный размер треугольника, сравнивая полную ширину клиентской области формы и ее высоту, деленную на соотношение. Меньшее из этих двух значений является наибольшим размером. Следующий метод должен быть добавлен в класс формы для вычисления размера треугольника. Обратите внимание, что высота уменьшается на два перед возвратом. Это позволит создать небольшую границу по краю фрактала.

Установка расположения вершин

Следующий метод рассчитает положения каждого из трех аттракторов, каждый из которых расположен в вершине треугольника. Эти значения будут основаны на размере треугольника и средней точке клиентской области формы. Средняя точка рассчитывается сначала с использованием половины высоты и ширины формы. Затем мы добавляем верхнюю вершину, которая будет нулевой точкой, координата X которой выровнена по вертикали со средней точкой, а координата Y равна половине высоты треугольника над средней точкой.

Две нижние вершины расположены на половине высоты треугольника ниже центра формы и на половине его ширины по обе стороны от этой точки. Это точки один и два в массиве.

Построение графиков вершин

Следующая задача — создать метод построения положения вершин. Это достигается за счет использования цикла «для каждого» для построения положения каждой точки по очереди. Фактический рисунок будет выполнен другим методом, в данном случае называемым «Точка построения», так как он будет повторно использован для построения точек во время создания фрактала. Обратите внимание, что оба этих метода принимают параметр, содержащий графическую поверхность, на которой нужно рисовать. Это будет создано, когда пользователь нажмет на кнопку.

Построение случайной точки

Предыдущие методы управляют инициализацией треугольника. Теперь мы можем создать методы, которые используются в цикле алгоритма для рисования фрактала. Метод DrawNextPoint будет управлять этим процессом, вызывая новый метод с именем «MoveTowardsRandomPoint», за которым следует вызов PlotPoint для размещения точки в текущем положении. Наконец, он вызывает приложение. Выполняйте события так, чтобы обновленный чертеж был виден.

MoveTowardsRandomPoint выбирает одну из трех вершин с помощью объекта рандомизатора. Затем он вычисляет положение, которое находится на полпути между текущим положением и выбранным аттрактором, и перемещается в эту точку. Добавьте два метода, описанных ниже, в класс формы:

Заключительная задача состоит в том, чтобы объединить все методы в событии нажатия кнопки формы. Добавьте приведенный ниже код в событие кнопки. Это начинается с получения графической области формы и размера треугольника. Размер используется для вычисления положений трех вершин и сохранения их в массиве. Как только три точки будут нанесены на график, будет задано начальное местоположение. В этом случае я использовал положение верхней вершины в качестве отправной точки.

Бесконечный цикл создается с помощью цикла while с условием, которое всегда будет истинным. В этом цикле повторно вызывается метод DrawNextPoint. В идеале вы должны создать цикл, который может быть остановлен пользователем.

Автор этого материала — я — Пахолков Юрий. Я оказываю услуги по написанию программ на языках Java, C++, C# (а также консультирую по ним) и созданию сайтов. Работаю с сайтами на CMS OpenCart, WordPress, ModX и самописными. Кроме этого, работаю напрямую с JavaScript, PHP, CSS, HTML — то есть могу доработать ваш сайт или помочь с веб-программированием. Пишите сюда.

заметки, си шарп, графики, алгоритмы, изображения

Содержание

C# Разработка
7 октября 2018 г.
Треугольник Серпинского методом хаоса. Программа на C# с исходным кодом.
Предыстория
Треугольник Серпинского методом хаоса.
Правила и примеры.
4 комментария:
Треугольник Серпинского
Некоторые свойства
Варианты
📸 Видео

Видео:Игры хаоса. Фракталы [Numberphile на русском]Скачать

C# Разработка

Блог о создании приложений на платформе .NET Framework

Видео:треугольник Серпинского наглядноСкачать

7 октября 2018 г.

Треугольник Серпинского методом хаоса. Программа на C# с исходным кодом.

Видео:Треугольник серпинского методом хаоса C# WINFORMSСкачать

Предыстория

Просматривая youtube, я наткнулся на интересное видео, в котором был показан пример создания фракталов используя очень простые правила:

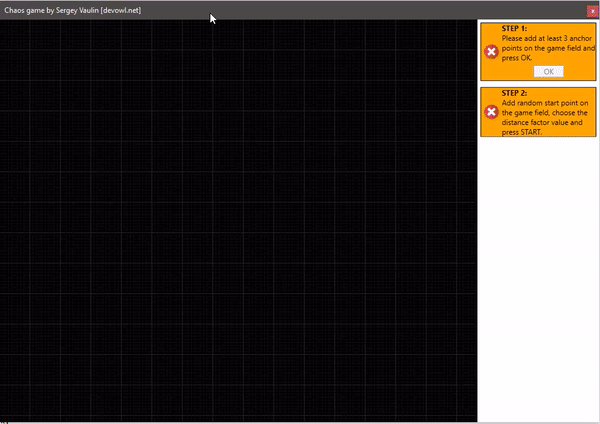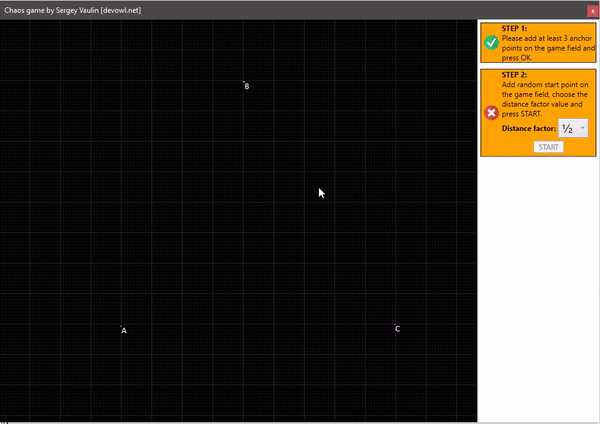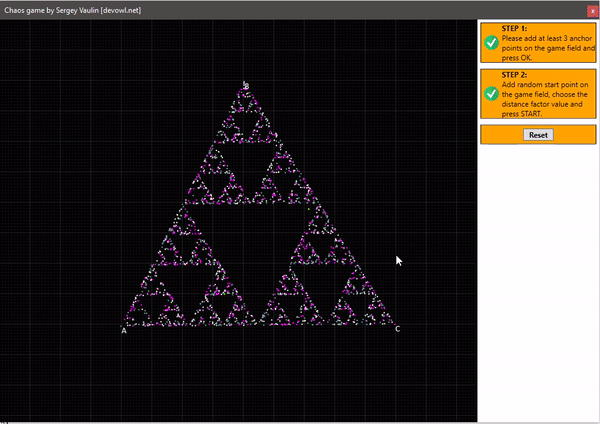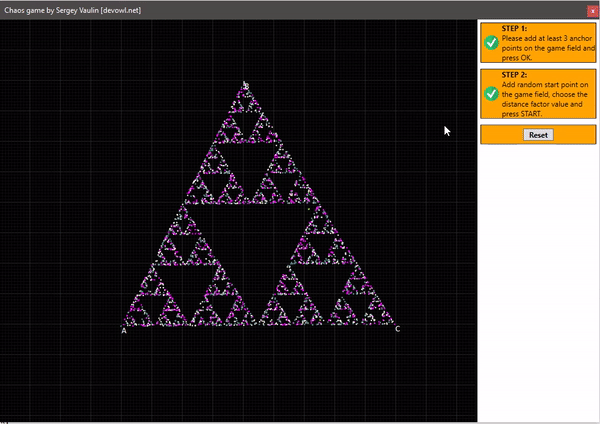
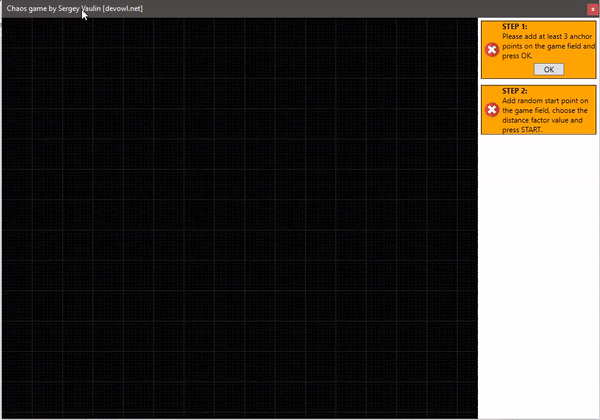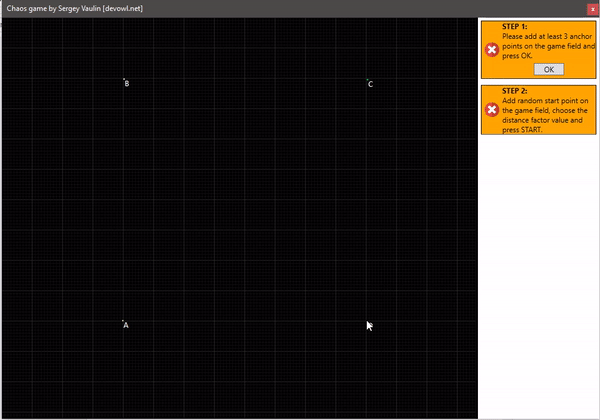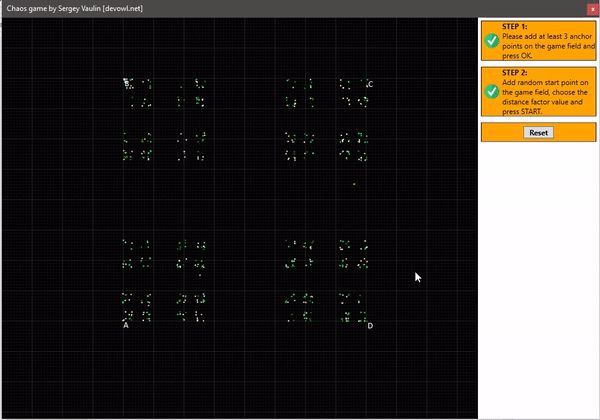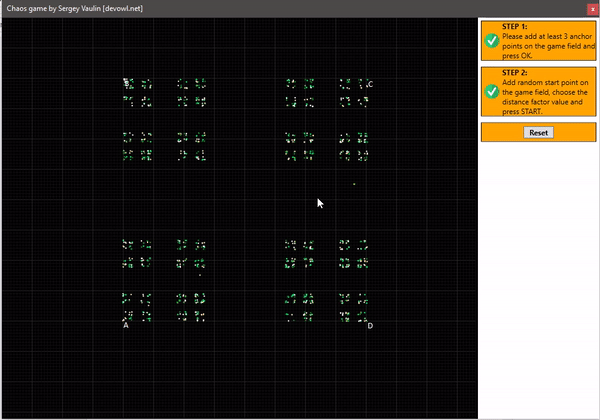
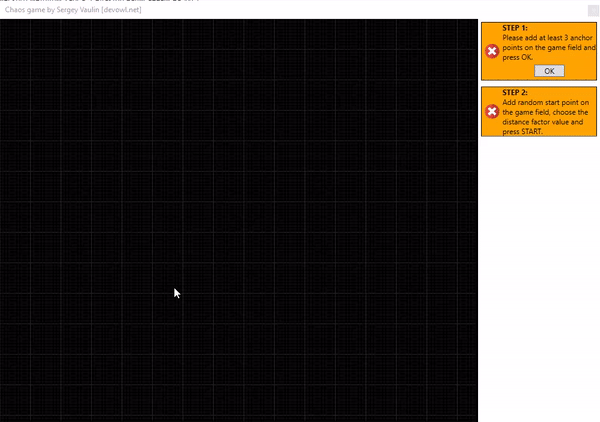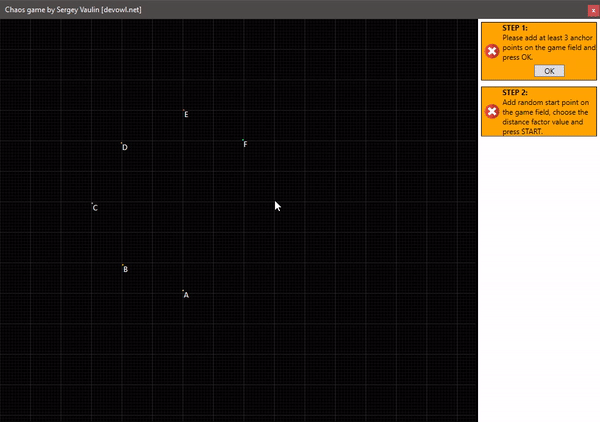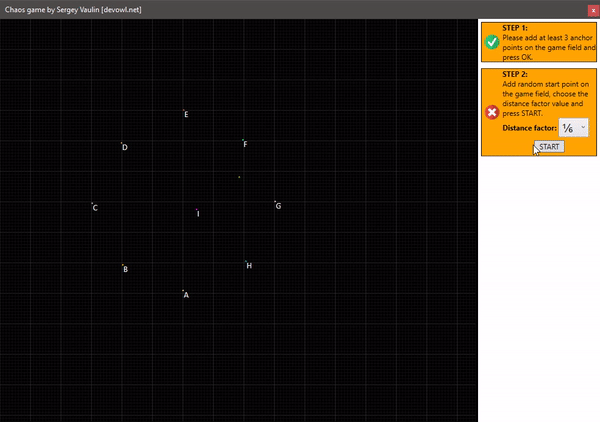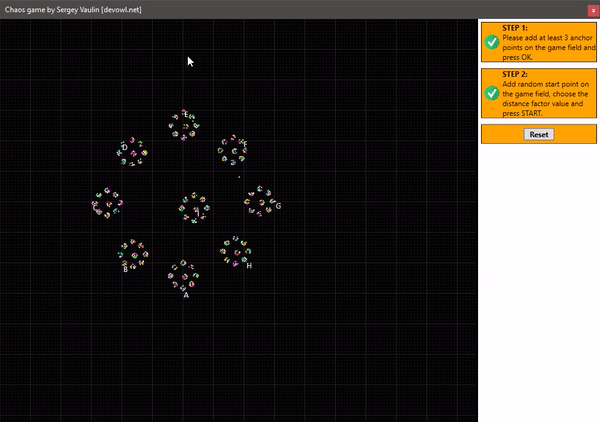
Мы имеем несколько опорных точек на плоскости. Все они пронумерованы.
Устанавливаем начальную произвольную точку с которой начнётся построение. Будем её называть текущей точкой.
Возьмём генератор случайных чисел в дапозоне от 1 до количества опорных точек. В зависимости от сгенерированного числа выбираем опорную точку под этим номером, после чего строим новую точку по середине (1/2 расстояния) от текущей до опорной точки. Это будет новая текущая точка для следущей итерации, после чего операцию повторяем действия до бесконечности.

Ссылка на то видео:

Видео:Построение треугольника СерпинскогоСкачать

Треугольник Серпинского методом хаоса.

Если следовать этим правилам, то на трёх точках мы получим достаточно интересный результат. Для этого мной было написано приложение, которое даёт возможность потестировать это, и увидеть воочию построение. Вот записанное видео с результатом:

Как видите, мы получили фигуру из само подобных треугольников, её научное название «треугольник Серпинского«. При этом удивительно, что у нас остаются не закрашенные области сколько бы раз мы не запускали приложение. Схематическое изображение треугольника представлено ниже:

И я считаю это удивительно получить столь изящную фигуру выбрасыванием случайного числа.

Видео:Треугольник Серпинского (фрактал) на JavaScriptСкачать

Правила и примеры.

Теперь представьте, что мы берём не середину расстояния (1/2) а к примеру треть (1/3), тогда можно увидеть не менее интересные картинки.

Построение для 3 точек:

Построение для 4 точек:

Построение круга с 1 центральной точкой и отступом 1/6:

На этом все, исходный код и само приложение можно найти по ссылке в начале статьи.

Спасибо за внимание!

4 комментария:

Поточечное прорисовывание электронами интерференционной картины за двумя щелями в эксперименте В. А. Фабриканта «отдыхает». В Википедии по поводу треугольника Серпинского есть ссылка на мою статью в журнале «В мире науки» (1989, №9.) Я с помощью элементарной цветографической символики в полной мере и геометрически наглядно вскрыл фрактальную организацию простых делителей в арифметическом треугольнике Паскаля. Так вот, точки единичных актов в построении т-ка Серпинского методом хаоса ложатся на «бесцветные перемычки» в цветографическом представлении распределения простого делителя 2 по степеням. То есть, на числа треугольника Паскаля, где он отсутствует. А в целом, построение т-ка Серпинского методом хаоса на элементарном (и потому особо ценном) уровне показывает, что такое нынешняя органичная фрактальная геометризация теории вероятностей. Ведь вероятность попадания очередного акта (очередной точки) на плоскости непосредственно выражается через фрактальную размерность т-ка Серпинского.

Я сам не программист, но есть одно предположение. Хотелось бы проверить. Можете сделать так, что бы последовательность случайных чисел (от 1 до 42) подгружалась из отдельного файла (например *.txt). А вершины треугольника можно было бы нумеровать несколькими цифрами: Вершина А (1,2. 14), вершина В (15,16. 28), вершина С (29,30. 42).

К сожалению пока такого рода доработку делать не буду

Видео:Треугольник Серпинского ФракталыСкачать

Треугольник Серпинского

Для просмотра анимации необходимо включить JavaScript.

Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. На рисунке показаны первые три шага, а на флэш-демонстрации вы можете потренироваться и получить шаги вплоть до десятого.

Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться «в обратном направлении»: взять изначально «пустой» треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т. д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут.

Следующий способ получить треугольник Серпинского еще больше похож на обычную схему построения геометрических фракталов с помощью замены частей очередной итерации на масштабированный фрагмент. Здесь на каждом шаге составляющие ломаную отрезки заменяются на ломаную из трех звеньев (она сама получается в первой итерации). Откладывать эту ломаную нужно попеременно то вправо, то влево. Видно, что уже восьмая итерация очень близка к фракталу, и чем дальше, тем ближе будет подбираться к нему линия.

Но и на этом не всё. Оказывается, треугольник Серпинского получается в результате одной из разновидностей случайного блуждания точки на плоскости. Этот способ называется «игрой Хаос». С его помощью можно построить и некоторые другие фракталы.

Суть «игры» такова. На плоскости зафиксирован правильный треугольник A₁A₂A₃. Отмечают любую начальную точку B₀. Затем случайным образом выбирают одну из трех вершин треугольника и отмечают точку B₁ — середину отрезка с концами в этой вершине и в B₀ (на рисунке справа случайно выбралась вершина A₁). То же самое повторяют с точкой B₁, чтобы получить B₂. Потом получают точки B₃, B₄, и т. д. Важно, чтобы точка «прыгала» случайным образом, то есть чтобы каждый раз вершина треугольника выбиралась случайно, независимо от того, что было выбрано в предыдущие шаги. Удивительно, что если отмечать точки из последовательности B_i, то вскоре начнет проступать треугольник Серпинского. Ниже изображено, что получается, когда отмечено 100, 500 и 2500 точек.

Некоторые свойства

Фрактальная размерность log₂3 ≈ 1,584962. . Треугольник Серпинского состоит из трех копий самого себя, каждая в два раза меньше. Взаимное расположение их таково, что если уменьшить клеточки сетки в два раза, то число квадратиков, пересекающихся с фракталом, утроится. То есть N(δ/2) = 3N(δ). Если сначала размер клеток был 1, а с фракталом пересекалось N₀ из них (N(1) = N₀), то N(1/2) = 3N₀, N(1/4) = 3 2 N₀, . N(1/2 k ) = 3 k N₀. Отсюда получается, что N(δ) пропорционально , и по определению фрактальной размерности она равна как раз log₂3.
Треугольник Серпинского имеет нулевую площадь. Это означает, что в фрактал не влезет ни один, даже очень маленький, кружок. То есть, если отталкиваться от построения первым способом, из треугольника «вынули» всю внутренность: после каждой итерации площадь того, что остается, умножается на 3/4, то есть становится всё меньше и стремится к 0. Это не строгое доказательство, но другие способы построения могут только усилить уверенность, что это свойство всё-таки верно.
Неожиданная связь с комбинаторикой. Если в треугольнике Паскаля с 2 n строками покрасить все четные числа белым, а нечетные — черным, то видимые числа образуют треугольник Серпинского (в некотором приближении).

Варианты

Ковер (квадрат, салфетка) Серпинского. Квадратная версия была описана Вацлавом Серпинским в 1916 году. Ему удалось доказать, что любая кривая, которую можно нарисовать на плоскости без самопересечений, гомеоморфна какому-то подмножеству этого дырявого квадрата. Как и треугольник, квадрат можно получить из разных конструкций. Справа изображен классический способ: разделение квадрата на 9 частей и выбрасывание центральной части. Затем то же повторяется для оставшихся 8 квадратов, и т. д.

Как и у треугольника, у квадрата нулевая площадь. Фрактальная размерность ковра Серпинского равна log₃8, вычисляется аналогично размерности треугольника.

Пирамида Серпинского. Один из трехмерных аналогов треугольника Серпинского. Строится аналогично с учетом трехмерности происходящего: 5 копий начальной пирамиды, сжатой в два раза, составляют первую итерацию, ее 5 копий составят вторую итерацию, и т. д. Фрактальная размерность равна log₂5. У фигуры нулевой объем (на каждом шаге половина объема выбрасывается), но при этом площадь поверхности сохраняется от итерации к итерации, и у фрактала она такая же, как и у начальной пирамиды.

Губка Менгера. Обобщение ковра Серпинского в трехмерное пространство. Чтобы построить губку, нужно бесконечное повторение процедуры: каждый из кубиков, из которых состоит итерация, делится на 27 втрое меньших кубиков, из которых выбрасывают центральный и его 6 соседей. То есть каждый кубик порождает 20 новых, в три раза меньших. Поэтому фрактальная размерность равна log₃20. Этот фрактал является универсальной кривой: любая кривая в трехмерном пространстве гомеоморфна некоторому подмножеству губки. У губки нулевой объем (так как на каждом шаге он умножается на 20/27), но при этом бесконечно большая площадь.