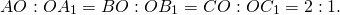Медиана циркулем в треугольнике

Что называется медианой треугольника?

Определение.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Как построить медиану треугольника?

Чтобы построить медиану треугольника , надо:

1) С помощью линейки найти и отметить середину стороны треугольника.

2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.

Рисунок медианы треугольника:

Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник».

Сколько медиан имеет треугольник?

Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.

Все три медианы треугольника пересекаются в одной точке:

Точка пересечения медиан называется центром тяжести треугольника.

В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины:

Об этом свойстве медиан треугольника, а также о том, как найти длину медианы через длины сторон треугольника, более подробно мы поговорим позже и рассмотрим, как свойства медианы использовать при решении задач.

Кроме того, отдельно будут рассмотрены медиана прямоугольного треугольника, проведенная к гипотенузе и медиана равнобедренного треугольника, проведенная к его основанию, поскольку каждая из них обладает своими свойствами, которые надо знать и уметь применять.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Построение медианы треугольника с помощью циркуля и окружности

Видео:Построение медианы в треугольникеСкачать

Как начертить медиану и высоту треугольника с помощью циркуля ?

Постройте треугольник ABC. Пусть необходимо провести медиану из вершины С к стороне AB.

Найдем середину стороны AB. Установите иглу циркуля в точке A. Другой конец циркуля поставьте в точку B. Тем самым ножками циркуля вы отмерили длину AB. Проведите окружность с центром в точке A и радиусом R, равным AB.

Затем, не меняя расстояния между ножкам циркуля, установите иглу циркуля в точке B. Проведите окружность с центром в точке В и тем же радиусом AB.

Окружности, проведенные из точек А и В, должны пересечься в двух точках. Назовите их, например, М и Т.

Соедините линейкой точки М и Т. Точка, в которой отрезок МТ пересечет отрезок АВ, и будет являться серединой отрезка АВ. Назовем эту точку точкой Е.

Кстати, прямая МТ будет не только делить отрезок АВ пополам, но и являться перпендикуляром к нему. Так что если перед вами стоит задача построить перпендикуляр к отрезку, действуйте по той же схеме, что и для нахождения середины отрезка.

Итак, поскольку Е — середина стороны АВ, то отрезок СЕ будет являться искомой медианой треугольника, проведенной из вершины С к стороне АВ. Соедините при помощи линейки точки С и Е.

Если необходимо провести также медианы из вершин треугольника А и В к сторонам ВС и АС соответственно, проделайте аналогичную процедуру. Помните, что все три медианы треугольника должны пересечься в одной точке.

В стороне от чертежа описывайте свои действия. Последовательно отмечайте, что вы строите. Какие линии, окружности вы проводите, и какими буквами обозначаете точки, получаемые на пересечениях.

В задачах на построение циркулем и линейкой обычно требуется не только построить что-либо, но и доказать, что используемая последовательность действий привела к нужному результату.

По построению четырехугольник АМВТ является ромбом (АМ=ВМ=АТ=ВТ=AB). Ромб — частный случай параллелограмма. Диагонали параллелограмма точкой пересечения делятся пополам (свойство параллелограмма) . То есть, точка Е, полученная на пересечении диагоналей ромба АВ и МТ, дает середину АВ. Т. к. точка Е — середина АВ, то СЕ — медиана треугольника АВС (по определению) . Что и требовалось доказать.

Вам надо определить ТОЧКУ, куда вести медиану и высоту? Или просто начертить? Начертить, так у циркуля с одной стороны остриё, а вот с другой карандаш (или рейсфедер) . Вот этим концом и чертите. А мединану надо определить среднюю сторону у противоположного угла. Циркулем произвольно чертите дуги с двух концов стороны, что бы они пересекались. И от противоположного угла проводите линию (медиану) с местам пересечения дуг (но до стороны треугольника, там и будет середина) . Высота прище. Делайте рисунок на листе в клетку. И от вершины вниз параллельно клеткам, т. е. перепендикулярно основанию треугольника.

Видео:Построение высоты в треугольникеСкачать

Медиана треугольника

Что называется медианой треугольника?

Определение.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Как построить медиану треугольника?

Чтобы построить медиану треугольника , надо:

1) С помощью линейки найти и отметить середину стороны треугольника.

2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.

Рисунок медианы треугольника:

Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник».

Сколько медиан имеет треугольник?

Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.

Все три медианы треугольника пересекаются в одной точке:

Точка пересечения медиан называется центром тяжести треугольника.

В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины:

Об этом свойстве медиан треугольника, а также о том, как найти длину медианы через длины сторон треугольника, более подробно мы поговорим позже и рассмотрим, как свойства медианы использовать при решении задач.

Кроме того, отдельно будут рассмотрены медиана прямоугольного треугольника, проведенная к гипотенузе и медиана равнобедренного треугольника, проведенная к его основанию, поскольку каждая из них обладает своими свойствами, которые надо знать и уметь применять.

Видео:Построение биссектрисы в треугольникеСкачать

Построение с помощью циркуля и линейки — описание, алгоритмы и задачи

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Построение отрезка, равного данному

Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.

Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

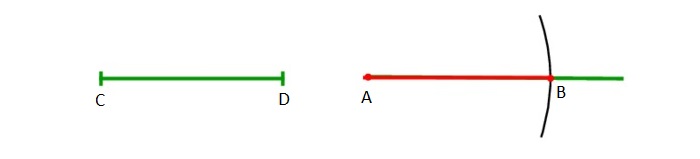
Деление отрезка пополам

Имеется отрезок AB.

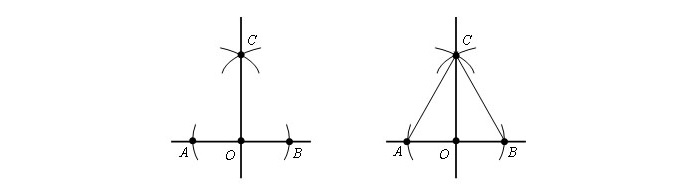
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

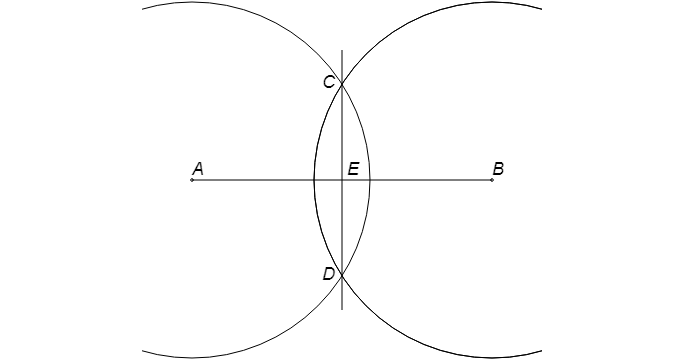
Построение угла, равного данному

Имеется угол ABC.

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Видео:Медиана треугольника. Построение. Свойства.Скачать

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O₁ — место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО₁ и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO₁A. Из данного вывода следует, что угол OAC = O₁AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O₁CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Видео:Задачи на построение с помощью циркуля и линейки - 7 класс геометрияСкачать

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

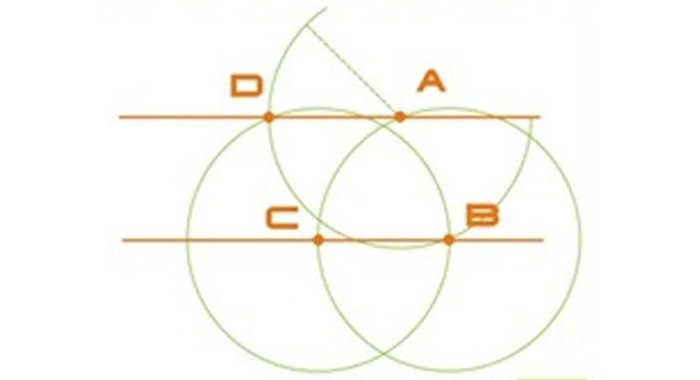
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Видео:Построение биссектрисы углаСкачать

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

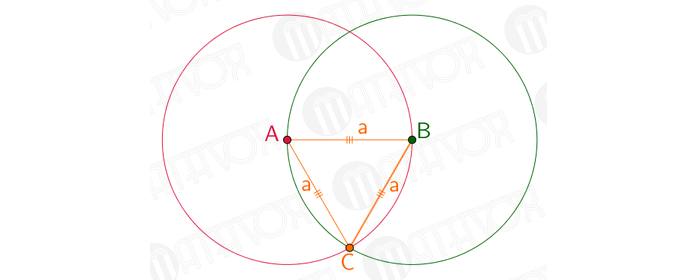
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Построение правильного четырехугольника вписанного в окружность

Вариант 1

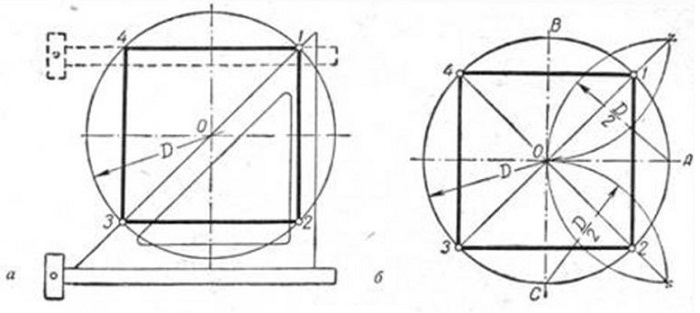
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

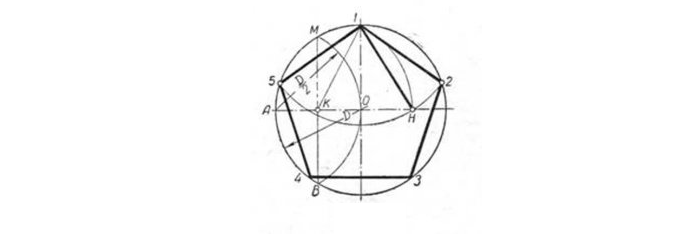
Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Видео:Построение биссектрисы угла. 7 класс.Скачать

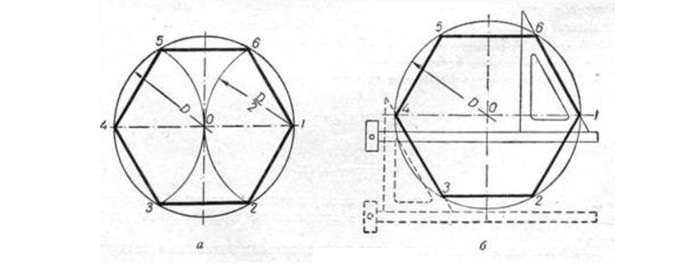
Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

Видео:Геометрия 7. Урок 10 - Построение циркулем и линейкойСкачать

Пошаговое построение медианы, биссектрисы медианы в треугольнике с помощью циркуля

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Поэтому, для построения медианы необходимо выполнить следующие действия:

1) найти середину стороны;

2) соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне. Поэтому, для построения биссектрисы необходимо выполнить следующие действия:

1) построить биссектрису какого-либо угла треугольника (а биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);

2) найти точку пересечения биссектрисы угла треугольника с противоположной стороной;

3) соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону. Поэтому, для построения высоты необходимо выполнить следующие действия:

1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);

2) из вершины, лежащей напротив проведенной прямой, опустить перпендикуляр к ней ( а перпендикуляр — это отрезок, проведенный из точки к прямой, составляющей с ней угол 90 градусов) — это и будет высота.

Задание для самостоятельной проверки.

1 вариант: Построить медиану остроугольного треугольника.

2 вариант: Построить медиану тупоугольного треугольника.

3 вариант: Построить медиану прямоугольного треугольника.

4 вариант: Построить биссектрису остроугольного треугольника.

5 вариант: Построить биссектрису тупоугольного треугольника.

6 вариант: Построить биссектрису прямоугольного треугольника.

📸 Видео

Построение высоты равнобедренного треугольника с помощью циркуля и линейкиСкачать

Построение биссектрисы углаСкачать

Треугольник: построение медианыСкачать

Построение медианы равнобедренного треугольника с помощью циркуляр линейкиСкачать

Построения с помощью циркуля и линейки. Равнобедренный и равносторонний треугольникиСкачать

2. Построения с помощью циркуля и линейки.Скачать