Медиана треугольника родовое понятие

Одно и то же математическое понятие может быть определено различными способами. Например, такое простейшее понятие, как «треугольник», в разных учебниках по математике определяется по-разному:

• Треугольник — это замкнутая ломаная линия, состоящая из трех звеньев»;
• Многоугольник, имеющий три стороны, называется треугольником;
• Если А, В и С — любые три точки, не лежащие на одной прямой, то объединение трех отрезков АВ, ВС и АС называется треугольником.

Все эти определения, как и ранее приведенное, правильные. Однако иногда, воспроизводя определения, имеющиеся в учебнике, или строя определения самостоятельно, ученики и, не только они, допускают разные ошибки. Чтобы строить и воспроизводить определения математических понятий правильно, нужно знать основные требования к логическому определению понятий.

Рассмотрим эти требования, попутно указывая наиболее часто встречающиеся ошибки в определении математических понятий.

Определения должны быть научно правильными.

Это означает, что, определяя то или иное понятие, надо это сделать так, чтобы не исказить научный смысл этого понятия. Так, например, смысл понятия «отношение» (в математике) состоит в том, что оно есть какое-то число. Между тем иногда это понятие определяют так: «Отношение есть сравнение двух чисел или величин посредством деления». Но сравнение есть некоторый процесс, а не число. В данном случае неверно выбрано родовое понятие и тем самым искажен научный смысл определяемого понятия. Другой пример. Иногда приходится слышать от ученика такое определение: «Абсолютной величиной, или модулем числа, называется это число без знака». Получается, что существуют какие-то числа без знака, но таких чисел (кроме нуля) математика не знает: в математике рассматриваются лишь положительные, отрицательные числа и нуль, других чисел нет. Если число написано без знака, то это положительное число, а не какое-то «беззначное». Поэтому приведенное определение неверное.

Определения не должны содержать «порочного круга».

Один ученик на вопрос, что такое умножение, например, ответил: «Умножением называется действие отыскания произведения». Когда же его спросили, а что такое произведение, он с уверенностью заявил, что это результат умножения. Следовательно, у этого ученика получается, что умножение определяется через понятие произведения, а произведение через понятие умножения. Получается «порочный круг» в определении. Ясно, что такой способ определения является грубо ошибочным. Еще пример ошибки «порочного круга» в определении: «Угол называется прямым, если его стороны перпендикулярны» и «Прямые называются перпендикулярными, если при пересечении они образуют прямые углы». Схему этих двух определений можно изобразить так.

Как видим, эти определения действительно образуют «порочный круг». Следовательно, строя определения математических понятий, надо следить за тем, чтобы они не образовали друг с другом «порочного круга».

Определение должно содержать указание на ближайшее родовое понятие.

Как бы ни было построено определение математического понятия, в нем должно быть указано ближайшее родовое понятие к определяемому понятию. Нарушение этого требования приводит к различным ошибкам. Так, например, иногда учащиеся, формулируя определения, вовсе не указывают родовое понятие. На вопрос, какие фигуры называется равновеликими, они отвечают: «Это если две фигуры имеют равные площади». Что означает «это», можно лишь догадываться. Или: на предложение сформулировать определение равнобедренных треугольников, иногда можно услышать такой ответ: «Это такие, у которых две стороны равны». Такая небрежность в формулировке определений недопустима. Другой тип ошибок связан с тем, что в определении указывается не ближайшее родовое понятие, а более широкое. Вот пример такого определения: «Параллелограмм есть фигура, у которой противоположные стороны параллельны». В этом определении указано не ближайшее для параллелограмма родовое понятие — «четырехугольник», а более далекое, более широкое — «фигура». И тем самым это определение становится неверным, ибо фигурой, у которой противоположные стороны параллельны, может быть не только параллелограмм, но и, например, правильный шестиугольник. Или другой пример. Давая определение диаметра круга, ученик сформулировал его так: «Диаметр круга есть прямая, проходящая через центр круга». Ученик указал в качестве родового понятия прямую, а ведь диаметр — это не вся прямая, а лишь отрезок прямой.

Определение не должно быть тавтологией, т. е. повторяющей в иной словесной форме ранее сказанное.

Сущность такой ошибки заключается в том, что понятие определяется через само себя. Вот примеры тавтологии в некоторых определениях: «Сложением называется действие, при котором числа складываются»(здесь сложение определено через понятие «складывание», что одно и то же). «Фигура А называется симметричной фигуре В, если они расположены симметрично относительно оси симметрии» (здесь «симметричные фигуры» определены через понятие «фигуры, расположенные симметрично»). Ясно, что такие определения являются грубо ошибочными.

Определение должно быть достаточным.

Это означает, что в определении должны быть указаны все признаки, позволяющие однозначно выделить объекты определяемого понятия. Если же это требование нарушается, то под определение можно подвести не только объекты определяемого понятия, но и другие объекты. Так, например, иногда ученики дают такое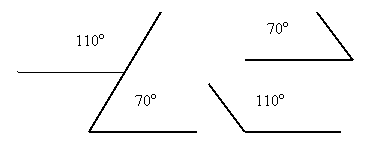определение смежных углов: «Смежными называются углы, которые в сумме составляют 180°». Недостаточность этого определения становится очевидной, если взглянуть на рисунок. На нем изображены две пары углов, сумма которых равна 180°, но они не смежные. Ошибка здесь в том, что указано лишь одно свойство смежных углов, оно недостаточно для их определения. Можно было бы, например, так определить их: «Смежными называются два угла, имеющие общую сторону, которые расположены в разных полуплоскостях от этой общей стороны и в сумме составляют 180°».

Например, медиану треугольника определили следующим образом: «Медианой треугольника называется отрезок, делящий его сторону пополам». Очевидно, что и в этом определении указано недостаточное число признаков медианы. Поэтому под это определение подходят не только медиана треугольника, но и средняя линия (ведь и она делит сторону треугольника пополам) и вообще любой отрезок, делящий сторону треугольника пополам. Для построения правильного определения медианы треугольника надо добавить еще и такой признак: «Медиана выходит из вершины треугольника». Тогда получаем такое правильное определение: «Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны».

Определение не должно быть избыточным.

Это означает, что в определении не должно быть указано лишних признаков, являющихся следствием других признаков определяемого понятия. Например, весьма часто встречается такое определение ромба: «Ромбом называется параллелограмм, все стороны которого равны между собой». Это определение явно избыточное, ибо достаточно равенства двух смежных сторон параллелограмма для того, чтобы были равны все его стороны. Следовательно, правильнее определять ромб следующим образом: «Ромбом называется параллелограмм, две смежные стороны которого равны». Вот другой пример: «Диаметром круга называется наибольшая хорда, проходящая через центр круга». Здесь первый признак «наибольшая» является следствием второго признака «проходящая через центр», а второй является следствием первого. Поэтому правильное определение такое: «Диаметром круга называется хорда, проходящая через центр круга» или: «Диаметром крута называется наибольшая хорда».

Мы указали лишь основные требования к определению математических понятий и привели примеры ошибок, возникающих при нарушении этих требований. Для того чтобы избежать таких ошибок, надо знать эти требования, учитывать их при формулировании тех или иных определений, учиться строить правильные определения.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Видео:8. Медиана треугольника и её свойства.Скачать

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Видео:Медиана треугольника. Построение. Свойства.Скачать

Медиана — это золотое сечение треугольника

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком понятии в математике, как МЕДИАНА.

У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.

И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.

Видео:🔥 Свойства МЕДИАНЫ #shortsСкачать

Медиана — это.

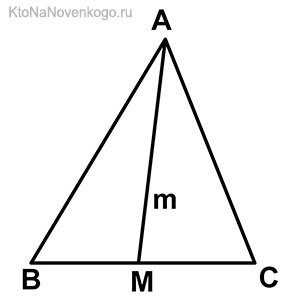
Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.

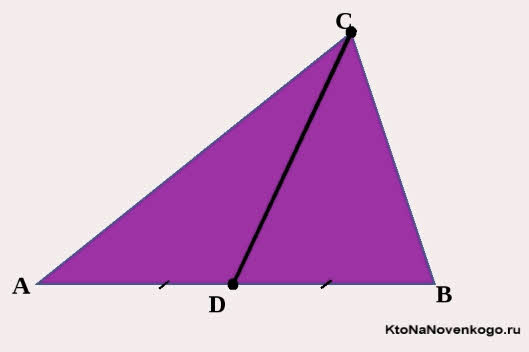
Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.

Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.

Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.

Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:

Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.

Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.

И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!

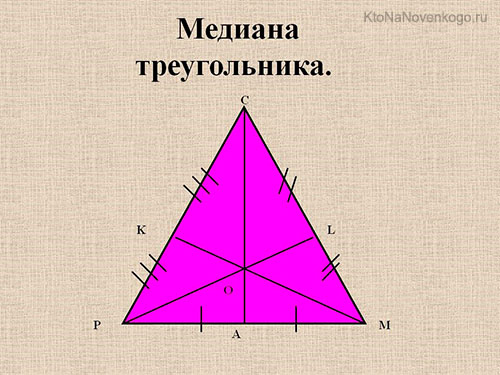
И выглядят они вот так.

На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.

Видео:Задача про медиану треугольника и периметры. Геометрия 7 класс.Скачать

Пересечение медиан треугольника

Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.

Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.

Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.

Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:

1. Отрезок СО вдвое больше, чем отрезок АО;
2. Отрезок РО вдвое больше, чем отрезок LO;
3. Отрезок МО вдвое больше, чем КО.

Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.

Видео:Длина медианы треугольникаСкачать

Медиана равностороннего треугольника

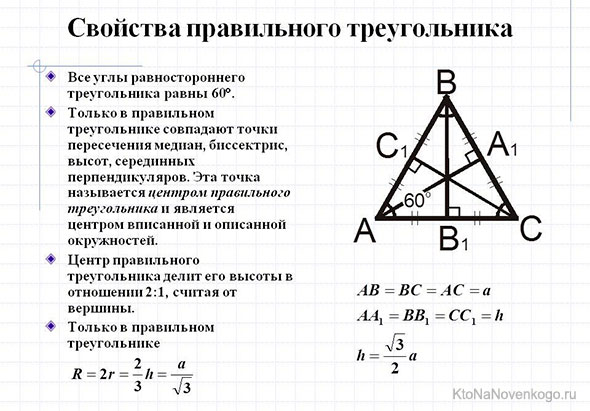
Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.

Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.

Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.

И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.

Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.

Видео:Построение медианы в треугольникеСкачать

Медиана прямоугольного треугольника

Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.

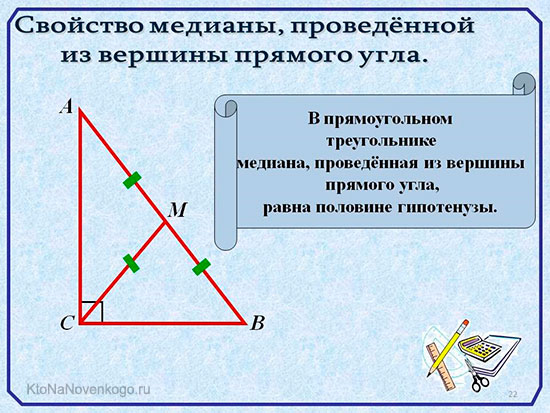
Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.

Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.

Видео:Свойство медианы в прямоугольном треугольнике #shortsСкачать

Вместо заключения

А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.

Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.

Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».

И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.

Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Теперь остаётся подумать над тем, как применить это знание о медиане на практике. Если придумаю, вдруг Нобелевскую премию дадут?

🎬 Видео

длина медианы #SHORTSСкачать

Медиана треугольникаСкачать

Все свойства медианы в одной задаче.Скачать

Точка пересечения медиан в треугольникеСкачать

№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Все факты о медиане треугольника для ЕГЭСкачать

Формулы для медианы треугольникаСкачать

Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Простое и красивое доказательство свойства медианы прямоугольного треугольник #геометрия #математикаСкачать