Медиана прямоугольного треугольника задачи

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми ( Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.

• BC = 2AD
• AD = BD = DC

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Видео:Задача за секунду. ОГЭ геметрия. Медиана прямоугольного треугольникаСкачать

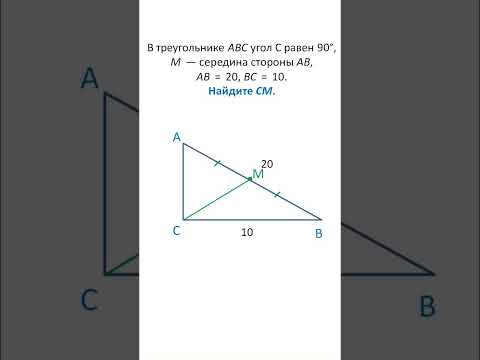
Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b 2 = с 2 – a 2 = 20 2 – 12 2 = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.

Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Решение задач по теме «Медиана прямоугольного треугольника»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Медиана прямоугольного треугольника. Теорема: Медиана прямоугольного треугольника проведенная из прямого угла, равна половине гипотенузы Дано: АВС – прямоугольный треугольник, O – середина АВ, СО — медиана, CO = ½AB = R Теорема (обратная): если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный. СО – медиана, СО = ½ АВ => АВС – прямоугольный.

Задача №2 Через основания биссектрис АD равнобедренного треугольника АВС с вершиной В проведен перпендикуляр к этой биссектрисе, пересекающей прямую АС в точке Е. Найдите отрезок АЕ, если известно, что СD = 4. Дано: АВС – равнобедренный треугольник. М – середина АЕ, СD = 4, DM = медиана, Найти: АЕ Решение: 1)DM – медиана прямоугольного треугольника АDE, проведенная из вершины прямого угла, => АМ = DM = МЕ, 2) угол ВАС = угол ВСА = α. По теореме о внешнем угле => треугольник DCM – равнобедренный. Следовательно, АЕ = 2DM = 2DC = 8 Ответ : 8.

Задача №1.2 Медиана, проведенная к гипотенузе прямоугольного треугольника, равна m и делит прямой угол в отношении 1:2. Найдите стороны треугольника. Дано: АВС – прямоугольный треугольник, угол C – прямой, CО = m Найти: АВ, ВС, СВ Решение: 1) 2)CО – медиана, по теореме AB=2m 3) По свойству прямоугольного треугольника: из АВС : АС = m 4) По теореме Пифагора: Ответ: 2m, m,

Задача №1.3 Медиана прямоугольного треугольника, проведенная к гипотенузе, разбивает его на два треугольника с периметрами 8 и 9. Найдите стороны треугольника. Дано АВС – прямоугольный треугольник, СО – медиана, РАСО = 8; РСОВ = 9. Найти: АВ, АС, СВ. Решение: 1) Обозначим через x – СО; тогда по теореме СО = АО = ОВ = x y – AC; CB – z. 2) РАСО = АС + АО + СО; РСОВ = CB + OB + CO; AC + AO + CO = 8 AC + 2x = 8 AC = 8 – 2x AC > CB CB + OB + CO = 9; CB + 2x = 9; CB = 9 – 2x; CB = 1 + AC; 3) => x=2,5 Ответ: 3, 4, 5.

№1.4. В треугольнике ABC к стороне AC проведены высота BK и медиана MB, причем AM=BM. Найдите косинус угла KBM, если AB=1, BC=2. Дано: ABC; BK – высота, MB – медиана, AM=BM; AB=1, BC=2. Найти: cosKBM. Решение: 1) По условию AM=BA MAB= MBA; ABM – равнобедренный. 2) AM=MC=BM BAC – прямоугольный. 3) BM= 4) Из 5) Из Ответ:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 988 человек из 78 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 68 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 673 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 537 538 материалов в базе

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 24.08.2016
• 465
• 0

• 24.08.2016
• 482
• 0

• 24.08.2016
• 334
• 0

• 24.08.2016
• 867
• 4

• 24.08.2016
• 2138
• 6

• 24.08.2016
• 543
• 0

• 24.08.2016
• 447
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 24.08.2016 9642
• PPTX 179 кбайт
• 33 скачивания
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Шараева Снежанна Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 9 месяцев
• Подписчики: 0
• Всего просмотров: 16398
• Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Володин призвал выработать единые нормы организации групп продленного дня

Время чтения: 2 минуты

В Курской области с 7 по 20 февраля ввели дистанционное обучение для школьников

Время чтения: 1 минута

В Оренбурге продлили дистанционное обучение для школьников

Время чтения: 1 минута

В России классы будут переводить на дистант, если заболели 20% детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Задачи репетитора по математике на свойства медиан

by Колпаков А.Н. on 30 июня 2013

Публикую свежий комплект заданий, предназначенный для урока геометрии в 8 классе. В распоряжение репетитора по математике передается 14 задач среднего уровня школьной сложности на центр тяжести треугольника и свойства его медиан. Решайте сами, решайте с репетитором. Дружите с математикой! Удачи.

Комплект предназначен для уроков

• Подготовки к ЕГЭ
• Подготовки к ГИА
• Устранения пробелов с репетитором по математике в 8 классе.
• Дополнительной практики решения задач по планиметрии

1) В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если АМ=2 и BN=3.

2) В треугольнике АВС медианы ВМ и АN пересекаются в точке P. Найдите их длины, если =36 кв.см. и AP-PM=1.

3) Найдите площадь треугольника АВС, если АВ=6см и ВС=8 см, а длина медианы ВМ равна 5см.

4) Найдите площадь треугольника MNP, если MN=5см, NP=12 см, NE- медиана и

5) Найдите площадь треугольника АВС, если АВ=16см, ВL – медиана и BL=17,

6) Найдите площадь треугольника, если известно. Что длины его двух медиан равны 6см и 9 см, а сами медианы перпендикулярны.

7) В треугольнике АВС: AB=6см, BC=8см, медианы АМ и CN образуют угол в . Найдите длину стороны АС

8) В треугольнике APC проведены две медианы PK и AD, пересекающиеся в точке E. Известно, что ; и . Найдите

9) В треугольнике MNK проведены две медианы MD и KP, пересекающиеся в точке С. Известно. Что MD=12см и расстояние от точки P до MD равно 8. Найдите

10) В треугольнике MDC проведены две медианы MK и DE, которые пересекаются в точке N. Найдите , если и

11) Точка А – точка пересечения медиан в треугольнике PNK. Найдите высоту треугольника, опущенную из точки N на сторону PK, если расстояние от А до PK=2см.

12) Медианы SK и АН треугольника АSE пересекаются в точке О. Найдите , если = 24 кв.см.
Ответ: 2 кв.см.

13) Медианы KE и QB треугольника QKC пересекаются в точке H. Найдите площадь треугольника CBE, если кв.см.
Ответ: 18 кв.см.

14) Медианы ME и NA треугольника MNK пересекаются в точке С. Найдите площадь треугольника CEA, если кв.см.

Каждая задачка, которая предлагается школьнику, должна реализовывать те или иные учебно-методические замыслы репетитора по математике и вести к развитию каких-либо локальных навыков (логико-смысловых или преобразующих / вычислительных). Хороший комплект обязан содержать максимально разнообразный по составу список упражнений, охватывающий как можно тем, пройденных ранее. К примеру, если репетитор по математике берется за какое-нибудь новое свойство или понятие, то в задачах на его закрепление необходимо пересмотреть как можно большее число разных комбинаций с ранее изученными фактами или понятиями. Если с репетитором по математике была изучена тема «площадь», но желательно включить в список задач парочку задач на соответствующие формулы.

Репетиторы по математике редко строят уроки по рекомендованным методистами образцам. Почему? Если репетитор плохой — он вообще не задумывается о порядке и учебной ценности решаемых задач, а если репетитор толковый — ему может банально не хватить учебного времени. Временные ограничения постоянно вяжут руки репетиторам по математике. Приходится пропускать задачки, исключать из планов разборы доказательств и др. Использование данного комплекта подразумевает более-менее удобный временные условия для работы. Задачи подобраны с учетом принципа аналогии. Одна задача разбирается совместно с преподавателем, а соседняя задается на дом.

Александр Николаевич, профессиональный репетитор по математике. Москва. Строгино.

📺 Видео

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Свойство медианы в прямоугольном треугольнике. Практическая часть. 8 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Медиана прямоугольного треугольника— Геометрия ОГЭСкачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Медиана в прямоугольном треугольникеСкачать

Медиана прямоугольного треугольника | Задачи 1-11 | Решение задач | Волчкевич |Уроки геометрииСкачать

8. Медиана треугольника и её свойства.Скачать

Геометрия Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна ееСкачать

№404. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузеСкачать