Медиана прямоугольного треугольника равна биссектрисе (6 видео)

Свойства медианы в прямоугольном треугольнике с доказательствами

В этой статье мы рассмотрим свойства медианы в прямоугольном треугольнике, а также их доказательства.

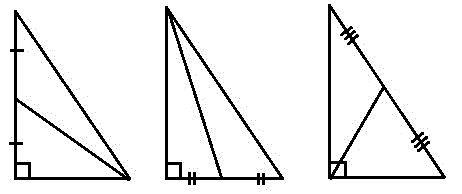
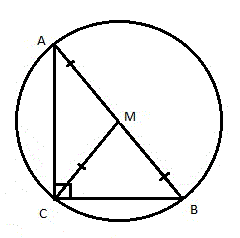
Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы (рис. 1).

Содержание

Свойства медианы в прямоугольном треугольнике
Доказательства свойств
Первое свойство
Доказательство:
Второе свойство
Доказательство:
Третье свойство
Доказательство:
Медиана треугольника является его биссектрисой
Все формулы медианы прямоугольного треугольника
🔍 Видео

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойства медианы в прямоугольном треугольнике

Медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана.
Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Доказательства свойств

Первое свойство

Доказать, что медианы в прямоугольном треугольнике пересекаются в одной точке и делятся в пропорции 2:1, считая от вершины.

Доказательство:

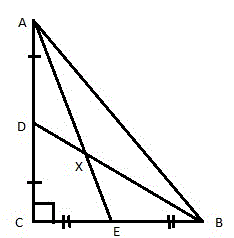
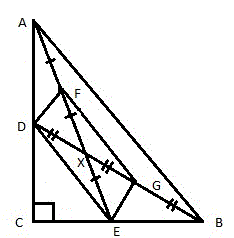
Рассмотрим прямоугольный треугольник ABC. Проведем две медианы AE и BD, которые пересекаются в точке X (рис. 2).

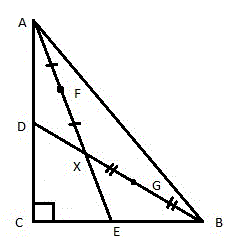
Середины отрезков AX и BX обозначим, соответственно, буквами F и G (рисунок 3).

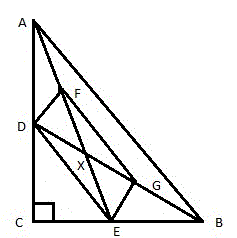
Соединим между собой точки (D, F, G и E) и получим четырёхугольник DFGE (рис. 4).

Сторона DE этого четырёхугольника будет средней линией треугольника ABC. Согласно определению: отрезок, соединяющий середины двух сторон треугольника, является его средней линией. При этом по свойству средняя линия параллельна не пересекающейся с ней стороне и равна половине этой стороны, то есть.
DE || AB и DE = AB / 2.

Аналогично сторона FG треугольника AXB будет его средней линией.
FG || AB и FG = AB / 2

Отсюда следует, что отрезки DE и FG являются параллельными и равными. Следовательно, четырехугольник DFGE – параллелограмм (по признаку параллелограмма).

Так как диагонали параллелограмма в точке пересечения делятся пополам, то
FX=XE, GX=XD

Так как AF = FX (по построению), то и AF = FX = XE, аналогично DX = XG = GB.

Получается, что точка X делит обе медианы AE и BD в соотношении 2 к 1 считая от вершины треугольника.

Аналогично, мы сможем доказать, что точка пересечения 3-ей медианы, проведенной из прямого угла к гипотенузе, с медианой AE (или BD) будет делить ее в соотношении 2 к 1, считая от вершины. То есть наша 3-я медиана также пройдет через точку X. Отсюда следует, что все 3 наши медианы пересекаются в одной точке.

Что и требовалось доказать.

Второе свойство

Доказать, что медиана, проведённая с вершины прямого угла к гипотенузе, равна половине гипотенузы.

Доказательство:

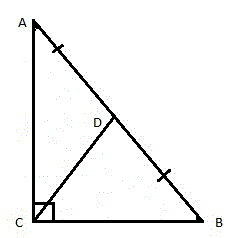
Чтобы доказать это свойство рассмотрим прямоугольный треугольник ABC и проведём медиану к гипотенузе. Точку ее пересечения с гипотенузой обозначим буквой D (рис. 6).

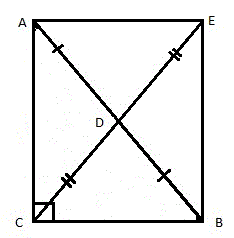
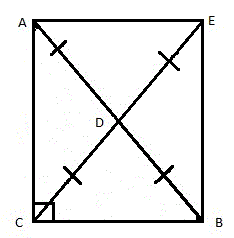
Отразим симметрично наш треугольник ABC относительно отрезка AB (рисунок 7). В результате получим четырёхугольник AEBC, в котором AD=DB (поскольку CD медиана к стороне AB) и CD=DE (по построению). То есть диагонали четырехугольника AEBC пересекаются и точкой пересечения делятся пополам. Отсюда следует, что AEBC является параллелограммом (по признаку параллелограмма).

Один из признаков прямоугольника говорит о том, что параллелограмм является прямоугольником, если хотя бы один из его углов прямой. Поскольку ∠ACB прямой (по построению), то AEBC — прямоугольник.

Поскольку диагонали прямоугольника равны и в точке пересечения делятся пополам (свойство прямоугольника), то AB = CE и AD = DB = CD = DE.

Так как AB = AD + DB, AD = BD и СD = AD = BD, то получается, что медиана AD, проведенная к гипотенузе AB равна половине ее длины.

Что и требовалось доказать.

Третье свойство

Доказать, что медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательство:

Опишем вокруг прямоугольного треугольника ABC окружность.

Поскольку точка C уже лежит на окружности, то для того, чтобы доказать, что медиана CM является радиусом, нам надо доказать, что точка M – центр описанной окружности (т.е. равноудалена от нее).

Так как медиана делит отрезок пополам, а медиана проведенная к гипотенузе равна ее половине (согласно доказанному выше свойству), то точка M будет равноудалена от всех вершин треугольника, которые в свою очередь касаются окружности (рисунок 8).

Отсюда следует, что окружность, описанная вокруг прямоугольного треугольника ABC будет иметь центр на середине гипотенузы (в точке M), а медиана CM будет радиусом описанной окружности.

Что и требовалось доказать.

Понравилась статья, расскажите о ней друзьям:

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Медиана треугольника является его биссектрисой

Выясним, какой вывод следует из того, что медиана треугольника является его биссектрисой?

Если медиана треугольника является его биссектрисой, то этот треугольник — равнобедренный.

Дано:

CK — медиана и биссектриса

Проведем анализ задачи.

На основе каких данных можно утверждать, что треугольник — равнобедренный? Если у него две стороны равны либо два угла равны. Значит, нам нужно доказать либо равенство сторон AC и BC, либо равенство углов A и B. Любое из этих равенств следует из равенства треугольников.

В треугольниках AKC и BKC биссектриса CK образует равные углы ACK и BCK, медиана CK — равные отрезки AK и BK. Сторона CK — общая.

Что мы имеем? Две стороны, но нет угла между ними. Ни к одной из сторон нет двух прилежащих углов. Признаки равенства треугольников применить не можем.

В таком случае придется выполнять дополнительные построения.

На луче CK отложим отрезок KE так, чтобы KE=CK, и точки A и E соединим отрезком. Получили еще один треугольник AKE.

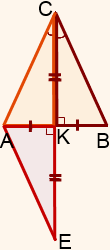
Мы можем доказать, что этот треугольник равен треугольнику BKC (по двум сторонам и углу между ними).

Из равенства этих треугольников следует равенство сторон AE и BC и углов AEK и BCK.

Получается, что в треугольнике ACE имеется два равных угла AEK и ACK. Поэтому он — равнобедренный, откуда легко доказывается и равенство сторон AC и ВС. Осталось записать доказательство.

На луче CK отложим отрезок KE, KE=CK.

Рассмотрим треугольники AKE и BKC:

1) AK=BK (так как CK — медиана по условию)

2) KE=CK (по построению)

3) ∠AKE=∠BKC (как вертикальные).

Следовательно, ∆ AKE=∆ BKC (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AE=BC и соответствующих углов: ∠AEK=∠BCK.

По условию, ∠BCK=∠AСK. Поэтому ∠AEK=∠AСK.

Таким образом получили, что в треугольнике ACE два угла равны. Значит, ∆ ACE — равнобедренный с основанием CE (по признаку). Следовательно, его боковые стороны равны: AE=AC.

А поскольку уже доказали, что AE=BC, то и AС=BС. Поэтому ∆ ABC — равнобедренный с основанием AB (по определению).

Что и требовалось доказать.

Если в треугольнике совпадают медиана и биссектриса, проведенные к каждой из сторон, то такой треугольник — равносторонний (каждые две его стороны равны между собой, значит, равны все три стороны).

Видео:8. Медиана треугольника и её свойства.Скачать

Все формулы медианы прямоугольного треугольника

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.

Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b — катеты

α — острый угол CAB

Медиана равна радиусу и половине гипотенузы, ( M ):

Формула длины через катеты, ( M ):

Формула длины через катет и острый угол, ( M ):

🔍 Видео

ЕГЭ 2024 по математике. №1,17 Медиана, биссектриса, высота, серединный перпендикулярСкачать

ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Свойство биссектрисы треугольника с доказательствомСкачать

Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

ЕГЭ Математика. Угол между медианой и биссектрисой в прямоугольном треугольникеСкачать

Задание 9 ОГЭ от ФИПИСкачать

Высота, медиана, биссектриса треугольника. Как построить в треугольнике. Геометрия 7 классСкачать

Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

6 задания ЕГЭ по математике. Угол между медианой и биссектрисой в прямоугольном треугольнике.Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Медиана в прямоугольном треугольникеСкачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Формула для биссектрисы треугольникаСкачать

Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать