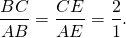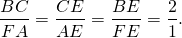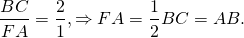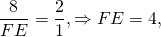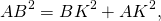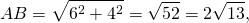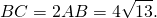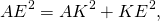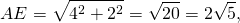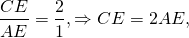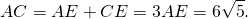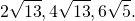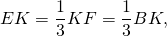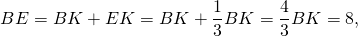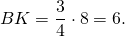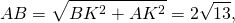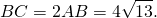Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Задание 26. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника ABC.
1. По условию задачи биссектриса BE и медиана AD пересекаются под прямым углом. Следовательно, в треугольнике ABD BO – медиана, и треугольник ABD равнобедренный с основанием AD. Тогда AO = OD = 4.
Если медиана с биссектрисой перпендикулярны, то в точке пересечения биссектриса делится в отношении 3:1, считая от вершины (по доказанной выше теореме), следовательно, BO = , OE = BE = 8 = 2
2. Рассмотрим прямоугольный треугольник AOB, в котором известны два катета AO и BO. По теореме Пифагора найдем гипотенузу AB:
Так как BD = AB, а BC = 2BD = 2AB, то BC =2∙ 2 = 4
3. Вычислим длину отрезка AE из прямоугольного треугольника AOE по теореме Пифагора: AE = = = = 2
По свойству биссектрисы треугольника =
и сторона AC = AE + EC = 2 + = 6
Курс повышения квалификации
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- В треугольнике биссектриса и медиана перпендикулярны
- Медиана перпендикулярна биссектрисе в треугольнике
- 📺 Видео
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 991 человек из 78 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 672 человека из 74 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 307 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Биссектриса перпендикулярна медианеСкачать
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 546 213 материалов в базе
Материал подходит для УМК
«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
§ 3. Применение подобия к доказательству теорем и решению задач
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 26.11.2017
- 2118
- 13
- 26.11.2017
- 2074
- 18
- 25.11.2017
- 461
- 0
- 25.11.2017
- 1000
- 2
- 25.11.2017
- 361
- 2
- 25.11.2017
- 1420
- 14
- 25.11.2017
- 2665
- 31
- 25.11.2017
- 2662
- 4
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 26.11.2017 5818
- DOCX 55.6 кбайт
- 19 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Туаева Марина Григорьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 4 года и 2 месяца
- Подписчики: 0
- Всего просмотров: 16179
- Всего материалов: 9
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:25 задание ОГЭ ✧ В ∆ABC биссектриса BE и медиана AD перпендикулярны и ... #огэ #егэ #геометрияСкачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Минпросвещения определило порядок получения заключений на международные договоры
Время чтения: 1 минута
Власти Бурятии заявили о нехватке школьных учителей и воспитателей
Время чтения: 2 минуты
Минобрнауки подготовит государственный рейтинг университетов
Время чтения: 1 минута
Петербургская учительница уволилась после чтения на уроке Введенского и Хармса
Время чтения: 3 минуты
В Госдуме предложили ввести пост уполномоченного по правам учителей
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

В треугольнике биссектриса и медиана перпендикулярны
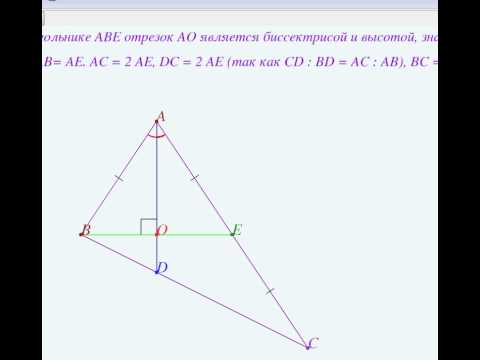
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8.
Найти стороны треугольника ABC.
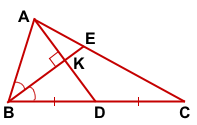
AD — медиана, BE — биссектриса,
Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD. Следовательно, BC=2AB.
По свойству равнобедренного треугольника BK — медиана и AK=KD=4.
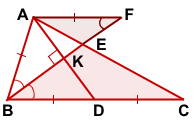
3) Проведём через точку A прямую, параллельную BC и продлим BE до пересечения с этой прямой в точке F.
Рассмотрим треугольники BEC и FEA.
∠AFB=∠CBF (как внутренние накрест лежащие при BC || AF и секущей BF).
Значит треугольники BEC и FEA подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Таким образом, треугольник ABF — равнобедренный с основанием BF, а значит, его высота AK является также медианой и BK=KF.
4) Рассмотрим прямоугольный треугольник ABK. По теореме Пифагора
5) Рассмотрим прямоугольный треугольник AKE.
KE=BE-BK=8-6=2. По теореме Пифагора
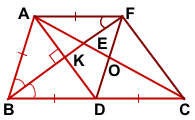
Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD.
По свойству равнобедренного треугольника BK — медиана и AK=KD=4.
2) Отложим на луче BE с другой стороны от точки K отрезок KF, KF=BK.
Проведём отрезки DF и CF.
Четырёхугольники AFDB и AFCD — параллелограммы (по признаку параллелограмма). Тогда AF=BD, DF=AB, FC=AD (по свойству параллелограмма), а так как AB=BD, то ABCD — ромб.
AC∩DF=O. По свойству параллелограмма O — середина DF. Значит E — точка пересечения медиан треугольника AFD. По свойству медиан FE:EK=2:1. Следовательно
3) Из треугольника ABK по теореме Пифагора
4) Так как сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, в параллелограмме AFCD
Видео:Геометрия В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длинуСкачать

Медиана перпендикулярна биссектрисе в треугольнике
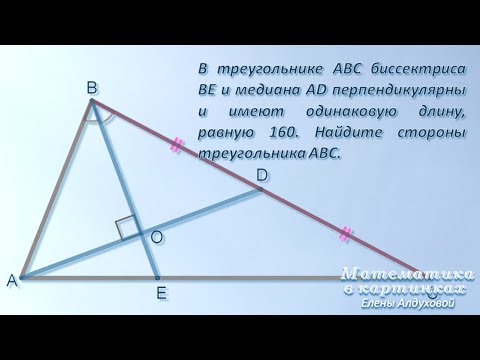
Задание 26. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника ABC.
1. По условию задачи биссектриса BE и медиана AD пересекаются под прямым углом. Следовательно, в треугольнике ABD BK – медиана, и треугольник ABD равнобедренный с основанием AD. Тогда AK=KD=4.
2. Так как AD – медиана, то BD=DC и из равенства AB=BD имеем:
3. По свойству биссектрисы треугольника ABC, имеем:
и, так как BC/AB = 2, то
4. Сделаем дополнительное построение: из точки A проведем прямую, параллельную BC до пересечения ее с продолжением биссектрисы BE в точке F. Получаем прямую 
Рассмотрим треугольник ABF, у которого AB=AF и углы при основании BF равны, следовательно, ABF – равнобедренный и AK – медиана этого треугольника: BK=KF. Из ранее записанного отношения:
Значит, BE+FE=8+4=12 и BK=KF=12:2 = 6.
5. Рассмотрим прямоугольный треугольник AKB, в котором известны два катета AK и BK. По теореме Пифагора найдем гипотенузу AB:

Так как BD=AB, а BC=2BD=2AB, то

6. Вычислим длину отрезка AE из прямоугольного треугольника AKE по теореме Пифагора:
По свойству биссектрисы треугольника можно записать, что

и сторона AC равна

Ответ: 
📺 Видео
Геометрия Задача № 25 ОГЭ 2021Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

ОГЭ, задание #26, вариант-8Скачать

Построение медианы в треугольникеСкачать

3 свойства биссектрисы #shortsСкачать

Задание 25 из реального ОГЭ по математике 2023 | УмскулСкачать

ЕГЭ 2024 по математике. №1,17 Медиана, биссектриса, высота, серединный перпендикулярСкачать

🔥 Свойства МЕДИАНЫ #shortsСкачать

Длина медианы треугольникаСкачать

ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

7 класс - Геометрия - Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольникаСкачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

@В Треугольнике биссектриса перпендикулярен медиану найти сторона ВС=? #geometryСкачать

17. Медианы, биссектрисы и высоты треугольникаСкачать

ОГЭ по математике. Задача 26Скачать