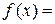Matlab треугольник на графике (4 видео) | Курс школьной геометрии

Глава 3. Работа с графиками в MatLab

MatLab предоставляет богатый инструментарий по визуализации данных. Используя внутренний язык, можно выводить двумерные и трехмерные графики в декартовых и полярных координатах, выполнять отображение изображений с разной глубиной цвета и разными цветовыми картами, создавать простую анимацию результатов моделирования в процессе вычислений и многое другое.

Функция plot

Рассмотрение возможностей MatLab по визуализации данных начнем с двумерных графиков, которые обычно строятся с помощью функции plot(). Множество вариантов работы данной функции лучше всего рассмотреть на конкретных примерах.

Предположим, что требуется вывести график функции синуса в диапазоне от 0 до . Для этого зададим вектор (множество) точек по оси Ox, в которых будут отображаться значения функции синуса:

В результате получится вектор столбец со множеством значений от 0 до и с шагом 0,01. Затем, вычислим множество значений функции синуса в этих точках:

и выведем результат на экран

В результате получим график, представленный на рис. 3.1.

Представленная запись функции plot() показывает, что сначала записывается аргумент со множеством точек оси Ох, а затем, аргумент со множеством точек оси Oy. Зная эти значения, функция plot() имеет возможность построить точки на плоскости и линейно их интерполировать для придания непрерывного вида графика.

Рис. 3.1. Отображение функции синуса с помощью функции plot().

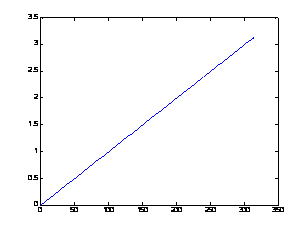
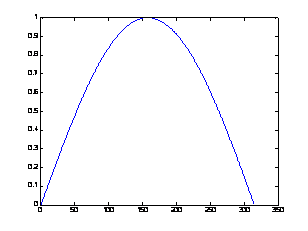
Функцию plot() можно записать и с одним аргументом x или y:

в результате получим два разных графика, представленные на рис. 3.2.

Анализ рис. 3.2 показывает, что в случае одного аргумента функция plot() отображает множество точек по оси Oy, а по оси Оx происходит автоматическая генерация множества точек с единичным шагом. Следовательно, для простой визуализации вектора в виде двумерного графика достаточно воспользоваться функцией plot() с одним аргументом.

Для построения нескольких графиков в одних и тех же координатных осях, функция plot() записывается следующим образом:

x = 0:0.01:pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1,x,y2);

Результат работы данного фрагмента программы представлен на рис. 3.3.

Рис. 3.2. Результаты работы функции plot() с одним аргументом:

а – plot(x); б – plot(y).

Рис. 3.3. Отображение двух графиков в одних координатных осях.

Аналогичным образом можно построить два графика, используя один аргумент функции plot(). Предположим, что есть два вектора значений

y1 = sin(x);
y2 = cos(x);

которые требуется отобразить на экране. Для этого объединим их в двумерную матрицу

в которой столбцы составлены из векторов y1 и y2 соответственно. Такая матрица будет отображена функцией

plot([y1’ y2’]); % апострофы переводят вектор-строку
% в вектор-столбец

в виде двух графиков (рис. 3.4).

Рис. 3.4. Отображение двумерной матрицы в виде двух графиков.

Два вектора в одних осях можно отобразить только в том случае, если их размерности совпадают. Когда же выполняется работа с векторами разных размерностей, то они либо должны быть приведены друг к другу по числу элементов, либо отображены на разных графиках. Отобразить графики в разных координатных осях можно несколькими способами. В самом простом случае можно создать два графических окна и в них отобразить нужные графики. Это делается следующим образом:

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

plot(x1, y1); % рисование первого графика
figure; % создание 2-го графического окна
plot(x2, y2); % рисование 2-го графика во 2-м окне

Функция figure, используемая в данной программе, создает новое графическое окно и делает его активным. Функция plot(), вызываемая сразу после функции figure, отобразит график в текущем активном графическом окне. В результате на экране будут показаны два окна с двумя графиками.

Неудобство работы приведенного фрагмента программы заключается в том, что повторный вызов функции figure отобразит на экране еще одно новое окно и если программа будет выполнена дважды, то на экране окажется три графических окна, но только в двух из них будут актуальные данные. В этом случае было бы лучше построить программу так, чтобы на экране всегда отображалось два окна с нужными графиками. Этого можно достичь, если при вызове функции figure в качестве аргумента указывать номер графического окна, которое необходимо создать или сделать активным, если оно уже создано. Таким образом, вышеприведенную программу можно записать так.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

figure(1); %создание окна с номером 1
plot(x1, y1); % рисование первого графика
figure(2); % создание графического окна с номером 2
plot(x2, y2); % рисование 2-го графика во 2-м окне

При выполнении данной программы на экране всегда будут отображены только два графических окна с номерами 1 и 2, и в них показаны графики функций синуса и косинуса соответственно.

В некоторых случаях большего удобства представления информации можно достичь, отображая два графика в одном графическом окне. Это достигается путем использования функции subplot(), имеющая следующий синтаксис:

Рассмотрим пример отображения двух графиков друг под другом вышеприведенных функций синуса и косинуса.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

x2 = 0:0.01:pi;
y2 = cos(x2);

figure(1);
subplot(2,1,1); % делим окно на 2 строки и один столбец
plot(x1,y1); % отображение первого графика
subplot(2,1,2); % строим 2-ю координатную ось
plot(x2,y2); % отображаем 2-й график в новых осях

Результат работы программы показан на рис. 3.5.

Аналогичным образом можно выводить два и более графиков в столбец, в виде таблицы и т.п. Кроме того, можно указывать точные координаты расположения графика в графическом окне. Для этого используется параметр position в функции subplot():

subplot(‘position’, [left bottom width height]);

где left – смещение от левой стороны окна; bottom – смещение от нижней стороны окна; width, height – ширина и высота графика в окне. Все эти переменные изменяются в пределах от 0 до 1.

Рис. 3.5. Пример работы функции subplot.

Ниже представлен фрагмент программы отображения графика функции синуса в центре графического окна. Результат работы показан на рис. 3.6.

x1 = 0:0.01:2*pi;
y1 = sin(x1);

subplot(‘position’, [0.33 0.33 0.33 0.33]);
plot(x1,y1);

В данном примере функция subplot() смещает график на треть от левой и нижней границ окна и рисует график с шириной и высотой в треть графического окна. В результате, получается эффект рисования функции синуса по центру основного окна.

Таким образом, используя параметр position можно произвольно размещать графические элементы в плоскости окна.

Рис. 3.6. Пример работы функции subplot с параметром position.

Оформление графиков

Пакет MatLab позволяет отображать графики с разным цветом и типом линий, показывать или скрывать сетку на графике, выполнять подпись осей и графика в целом, создавать легенду и многое другое. В данном параграфе рассмотрим наиболее важные функции, позволяющие делать такие оформления на примере двумерных графиков.

Функция plot() позволяет менять цвет и тип отображаемой линии. Для этого, используются дополнительные параметры, которые записываются следующим образом:

Обратите внимание, что третий параметр записывается в апострофах и имеет обозначения, приведенные в таблицах 3.1-3.3. Маркеры, указанные ниже записываются подряд друг за другом, например,

‘ko’ – на графике отображает черными кружками точки графика,
‘ko-‘ – рисует график черной линией и проставляет точки в виде кружков.

Табл. 3.1. Обозначение цвета линии графика

Маркер	Цвет линии
c	голубой
m	фиолетовый
y	желтый
r	красный
g	зеленый
b	синий
w	белый
k	черный

Табл. 3.2. Обозначение типа линии графика

Маркер	Цвет линии
—	непрерывная
—	штриховая
:	пунктирная
-.	штрих-пунктирная

Табл. 3.3. Обозначение типа точек графика

Маркер	Цвет линии
.	точка
+	плюс
*	звездочка
o	кружок
x	крестик

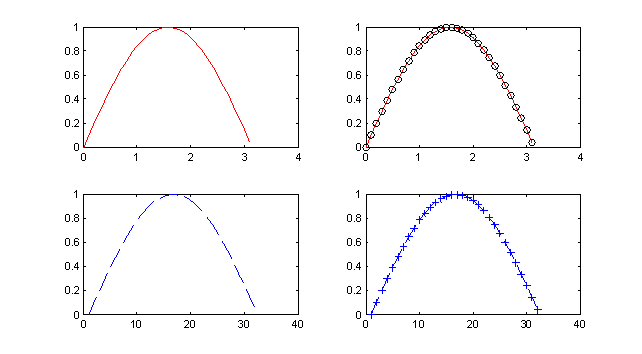
Ниже показаны примеры записи функции plot() с разным набором маркеров.

x = 0:0.1:2*pi;
y = sin(x);

subplot(2,2,1); plot(x,y,’r-‘);
subplot(2,2,2); plot(x,y,’r-‘,x,y,’ko’);
subplot(2,2,3); plot(y,’b—‘);
subplot(2,2,4); plot(y,’b—+’);

Результат работы фрагмента программы приведен на рис. 3.7. Представленный пример показывает, каким образом можно комбинировать маркеры для достижения требуемого результата. А на рис. 3.7 наглядно видно к каким визуальным эффектам приводят разные маркеры, используемые в программе. Следует особо отметить, что в четвертой строчке программы по сути отображаются два графика: первый рисуется красным цветом и непрерывной линией, а второй черными кружками заданных точек графика. Остальные варианты записи маркеров очевидны.

Рис. 3.7. Примеры отображения графиков с разными типами маркеров

Из примеров рис. 3.7 видно, что масштаб графиков по оси Ox несколько больше реальных значений. Дело в том, что система MatLab автоматически масштабирует систему координат для полного представления данных. Однако такая автоматическая настройка не всегда может удовлетворять интересам пользователя. Иногда требуется выделить отдельный фрагмент графика и только его показать целиком. Для этого используется функция axis() языка MatLab, которая имеет следующий синтаксис:

axis( [ xmin, xmax, ymin, ymax ] ),

где название указанных параметров говорят сами за себя.

Воспользуемся данной функцией для отображения графика функции синуса в пределах от 0 до :

x = 0:0.1:2*pi;
y = sin(x);

subplot(1,2,1);
plot(x,y);
axis([0 2*pi -1 1]);

subplot(1,2,2);
plot(x,y);
axis([0 pi 0 1]);

Из результата работы программы (рис. 3.8) видно, что несмотря на то, что функция синуса задана в диапазоне от 0 до , с помощью функции axis() можно отобразить как весь график, так и его фрагмент в пределах от 0 до .

Рис. 3.8. Пример работы функции axis()

В заключении данного параграфа рассмотрим возможности создания подписей графиков, осей и отображения сетки на графике. Для этого используются функции языка MatLab, перечисленные в табл. 3.4.

Таблица 3.4. Функции оформления графиков

Название	Описание
grid [on, off]	Включает/выключает сетку на графике
title(‘заголовок графика’)	Создает надпись заголовка графика
xlabel(‘подпись оси Ox’)	Создает подпись оси Ox
ylabel(‘подпись оси Oy’)	Создает подпись оси Oy
text(x,y,’текст’)	Создает текстовую надпись в координатах (x,y).

Рассмотрим работу данных функций в следующем примере:

x = 0:0.1:2*pi;
y = sin(x);

plot(x,y);
axis([0 2*pi -1 1]);
grid on;
title(‘The graphic of sin(x) function’);
xlabel(‘The coordinate of Ox’);
ylabel(‘The coordinate of Oy’);
text(3.05,0.16,’leftarrow sin(x)’);

Из результата работы данной программы, представленного на рис. 3.9, видно каким образом работают функции создания подписей на графике, а также отображение сетки графика.

Таким образом, используя описанный набор функций и параметров, можно достичь желаемого способа оформления графиков в системе MatLab.

Рис. 3.9. Пример работы функций оформления графика

Видео:MatLab. Урок 1. Основы программирования.Скачать

Matlab треугольник на графике

Обычная графика MATLAB

Построение графиков точками и отрезками прямых

Графики в логарифмическоми полулогарифмическом масштабе

Гистограммы и диаграммы

Графики специальных типов

Создание массивов данных для трехмерной графики

Построение графиков трехмерных поверхностей, сечений и контуров

Средства управления подсветкой и обзором фигур

Средства оформления графиков

Одновременный вывод нескольких графиков

Управление цветовой палитрой

Окраска трехмерных поверхностей

Двумерные и трехмерные графические объекты

Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.

Описанию графических функций и команд посвящена обширная электронная книга в формате PDF. Объем материала по графике настолько велик, что помимо вводного описания графики в уроке 3 в этой книге даются еще два урока по средствам обычной и специальной графики. Они намеренно предшествуют систематизированному описанию большинства функций системы MATLAB, поскольку графическая визуализация вычислений довольно широко используется в последующих материалах книги. При этом графические средства системы доступны как в командном режиме вычислений, так и в программах. Этот урок рекомендуется изучать выборочно или выделить на него не менее 4 часов.

Построение графиков отрезками прямых

Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.

Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.

plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.

Приведенный ниже пример иллюстрирует построение графиков двух функций — sin(x) и cos(x), значения функции которых содержатся в матрице Y, а значения аргумента х хранятся в векторе X:

На рис. 6.1 показан график функций из этого примера. В данном случае отчетливо видно, что график состоит из отрезков, и если вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.

Рис. 6.1. Графики двух функций в декартовой системе координат

plot(Y) — строит график у(г), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y). imag(Y)). Во всех других случаях мнимая часть данных игнорируется.

Вот пример использования команды plot(Y):

Соответствующий график показан на рис. 6.2.

Рис. 6.2. График функции, представляющей вектор Y с комплексными элементами

plot(X.Y.S) — аналогична команде plot(X.Y), но тип линии графика можно задавать с помощью строковой константы S.

Значениями константы S могут быть следующие символы.

Видео:MATLAB 01 Начало работыСкачать

Построение графиков.

Основная команда для построения графиков функций одной переменной в MATLAB – команда plot. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах (Figure).

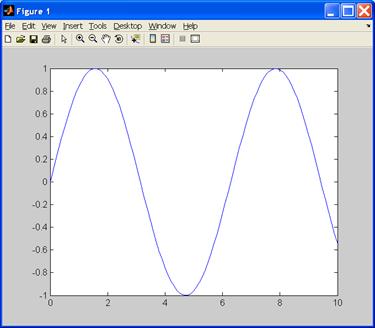
Возьмем вначале простейший пример – построим график синусоиды. Следует помнить, что MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между соседними точками. Зададим интервал изменения аргумента х от 0 до 10 с шагом 0.1.

Текст соответствующего M-файла:

x=0:0.1:10; y=sin(x); plot(x,y)

Графическое окно с результатом представлено на рис. 1.

Рис. 1. Графическое окно, в котором построен график синусоиды.

Дополнительные возможности для оформления графиков:

· hold on (hold off) – объединение (отключение) нескольких графиков на одних координатных осях;

· grid on (grid off) – нанесение (отключение) линий сетки на график;

· title(‘заголовок’) – вывод заголовка функции;

· xlabel(‘подпись под осью x’),ylabel(‘подпись под осью y’) – соответственно подписи осей х и у;

· text(m,n,’надпись’)– надпись в заданном месте рисунка, m и n – координаты точки на графике, начиная с которой выводится запись (координаты точки задаются в тех же единицах измерения, что и координаты осей графика);

· legend(‘легенда 1’, ‘легенда 2’, … , ‘легенда n’, k)– легенды для каждого из n-графиков k – местоположение легенды.

· Функцияsubplot(m,n,p) – это разделение графического окна MATLAB на несколько подокон с различными графиками, где m и n – число частей по вертикали и по горизонтали, на которые делится графическое окно, p – номер подокна в котором нужно отобразить график.

Полная форма команды построения графиков функций одной переменной:

где x1, x2, … , xn – массивы абсцисс графиков; y1, y2, …, yn – массивы ординат; s1, s2, … , sn – строка, состоящая из трех символов, которые определяют цвет линии, тип маркера и тип линии графиков.

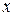
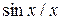
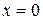
Кроме того, для построения графиков функций одной переменной можно использовать графическую функцию fplot. Она позволяет строить график функции, заданной в символьном виде (например, арифметическое выражение, определяющее функцию, заключено в апострофы), в интервале изменения аргумента от xmin до xmax без фиксированного шага изменения х. Рассмотрим ее применение для построения графика функции на интервале от -10 до 10. Эта функция имеет устранимую неопределенность в точке 0. Построение ее графика с помощью plot в этой точке не представляется возможным. Соответствующее графическое окно с графиком представлено на рис. 2. Заметим, что в точке результат правильный, т.е. .

Текст соответствующего M-файла:

fplot(‘sin(x)/x’,[-10,10]);grid on

Рис. 2. Графическое окно, в котором построен график sin(x)/x.

Команда grid on (сетка) позволяет включить отображение сетки, которая строится пунктирными линиями.

Таблица 1.6. Параметры для управления цветом и видом графиков.

Параметр	Обозначение
Тип линии
сплошная	—
пунктирная	:
штриховая	—
штрихпунктирная	-.
Цвет линии
красный	r
желтый	y
зеленый	g
синий	b
голубой	c
розовый	m
черный	k
белый	w
Тип маркера
точка	.
кружок	о
крестик	x
плюс	+
звездочка	*
квадрат	s
ромб	d
треугольник вершиной вниз	v
треугольник вершиной вверх	^