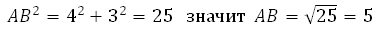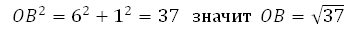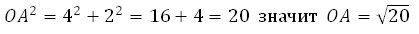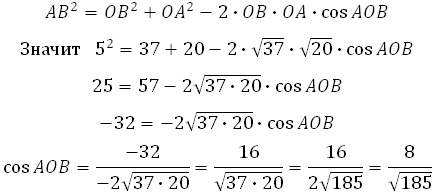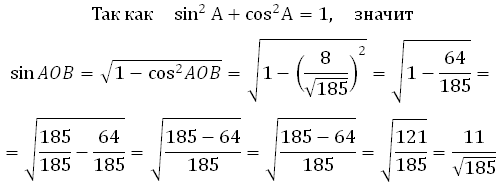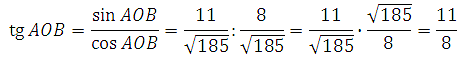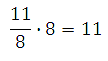Градусы треугольника по клеткам (8 видео)

Угол на клетчатой бумаге

Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.

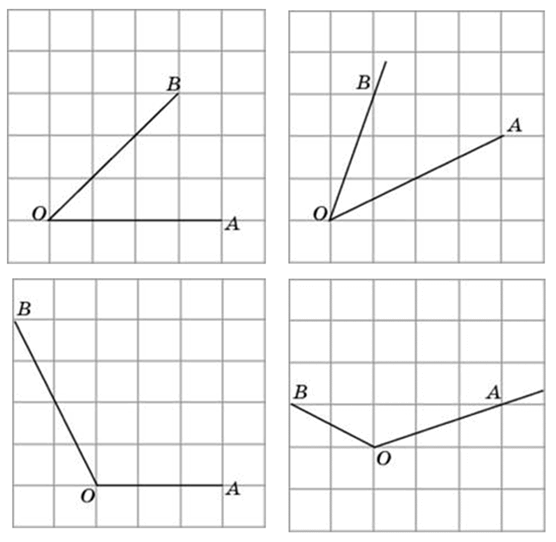
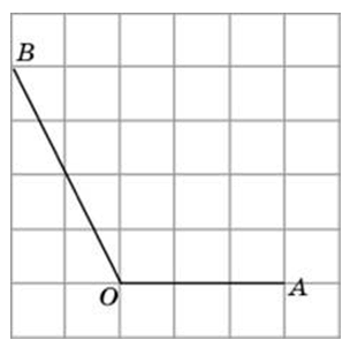
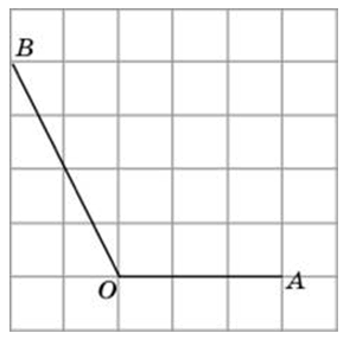
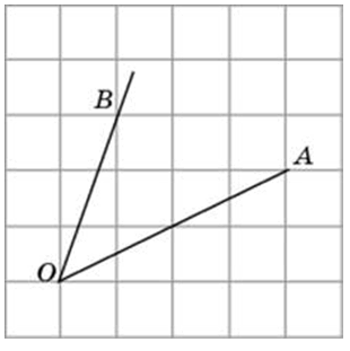
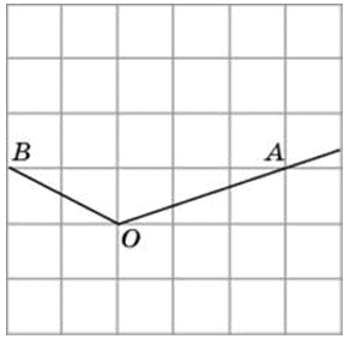
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):

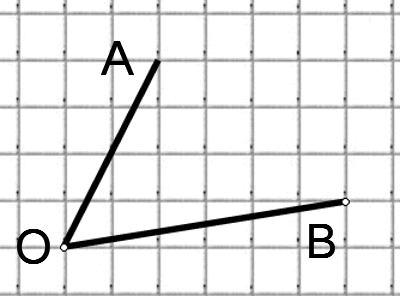
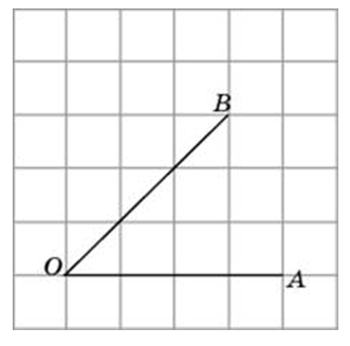
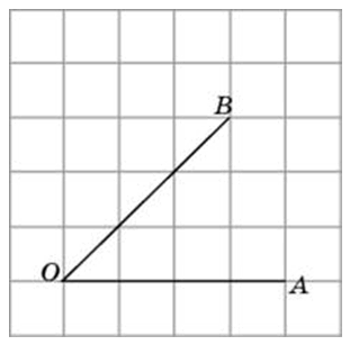
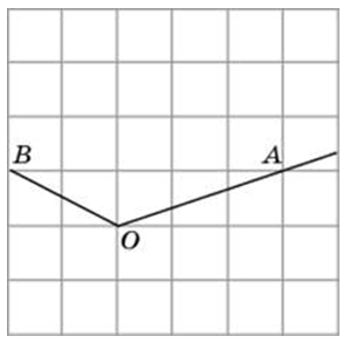
Итак, рассмотрим задание:

Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.

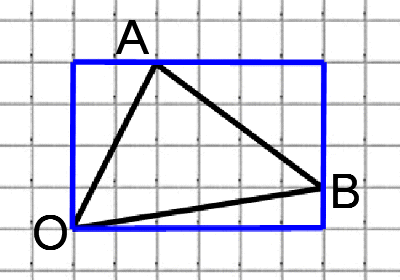
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.

Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).

АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,

ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,

OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,

По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.

Из основного тригонометрического тождества можем найти sin AOB:

*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.

Теперь можем найти тангенс:

Умножим результат на 8 и запишем ответ:

Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.

Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.

Найдите тангенс угла AOB.

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.

Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.

Найдите тангенс угла AOB.

В данной рубрике продолжим рассматривать задачи, не пропустите!

Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

Подготовка к ОГЭ. «Углы на клетках»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Углы на клетках

Как построить прямой угол по клеткам? Очень просто! – скажете вы. – Отметим точку, вершину угла, от неё чертим вправо или влево луч, затем ещё один луч вверх или вниз. Угол между горизонталью и вертикалью – прямой. А можно и по диагоналям соседних клеток.

Всё верно. А если один из лучей уже построен и он не горизонтальный, не вертикальный и не проходит по диагоналям клеток? Как начертить второй луч, чтобы угол между ними был прямым?

Найдём узел сетки, через который проходит начерченный луч. На нашем рисунке до такого узла от начала луча нужно пройти 3 клетки ВЛЕВО и 1 клетку ВНИЗ. Поэтому чтобы получился прямой угол, надо от начала луча отсчитать 1 клетку ВЛЕВО и 3 клетки ВВЕРХ. Почему? Обозначим упомянутые нами точки – А, В и О. Построим векторы ОА и ОВ. Координаты вектора ОА равны (-3; -1), вектора ОВ (-1; 3). Их скалярное произведение равно 0, поэтому они перпендикулярны.

Можно отсчитывать клетки и так: 1 клетку ВПРАВО и 3 клетки ВНИЗ. Тогда вектор ОВ имеет координаты (1; -3), при этом скалярное произведение векторов ОА и ОВ также равно 0.

Вывод. Векторы с координатами ( a ; b ) и (- b ; a ), или ( a ; b ) и ( b ; — a ), — перпендикулярны.

Рассмотрим несколько задач, связанных с умением находить прямой угол на рисунке.

№ 1 . Найти угол АВС на рисунке.

Решение. На первом рисунке угол АОС построен на диагоналях соседних клеток. На втором рисунке векторы ОА и ОС имеют координаты соответственно (3; -4) и (4; 3). Поэтому на первом и втором рисунках центральный угол АОС – прямой, а вписанный угол АВС, опирающийся на ту же дугу, равен его половине, то есть 45 ° . На третьем рисунке угол АОС – половина прямого, то есть 45 ° , а угол АВС соответственно равен 22,5 ° .

№ 2. Три квадрата расположены так, как показано на рисунке. Чему равен угол между прямыми АС и В D ?

Решение. Отрезок В D переместим параллельно вниз на одну клетку. Появляется отрезок АМ, равный В D . Угол между прямыми АС и В D равен углу между АС и АМ на втором рисунке. Соединим отрезком точки С и М. Получается, что угол АМС – прямой и АМ = МС. Треугольник АСМ прямоугольный равнобедренный, поэтому искомый угол равен 45°.

№ 3. Найти тангенс угла, изображенного на рисунке.

Решение. Выделим на этом рисунке узлы сетки – точки А и С. Рассмотрим треугольник АВС. Заметим, что он является прямоугольным, к тому же катет ВС в 2 раза больше катета АС. Отсюда следует, что тангенс угла В равен 1:2 = 0,5.

Правильный треугольник и описанная около неё окружность, построенные на клетках, несут в себе много интересных свойств. Известно, что радиус окружности, описанной около равностороннего треугольника со стороной а, равен , а радиус вписанной в него окружности — , то есть в два раза меньше. Отсюда следует, что хорда, перпендикулярная радиусу окружности и проходящая через его середину, является стороной правильного треугольника. Другими словами, острый вписанный угол, опирающийся на хорду, перпендикулярную радиусу и проходящую через его середину, равен 60 ° , а центральный угол и тупой вписанный угол, опирающиеся на эту хорду, — 120 ° .

Рассмотрим несколько примеров задач, решаемых на основе этого свойства.

Угол АВС на рисунке равен 60 ° , так как хорда АС проходит через середину радиуса и перпендикулярна ему.

Угол АВС на рисунке является половиной угла в 60 ° из предыдущей задачи и равен 30 ° .

Угол АВС на следующем рисунке равен 120 ° . При этом четырёхугольник АВСО является ромбом и его острый угол равен 60 °.

Полезным при решении задач на клетках является знание углов правильных многоугольников . Рассмотрим правильный шестиугольник и правильный восьмиугольник. Около них описаны окружности. Каждый внутренний угол правильного шестиугольника равен 120 ° , угол между диагоналями-диаметрами равен 60 ° , угол между двумя соседними диагоналями, исходящими из одной вершины, равен 30 ° , меньшая диагональ правильного шестиугольника перпендикулярна его стороне, а с другими соседними сторонами — угол 30 ° . Каждый угол правильного восьмиугольника равен 135 °, угол между соседними диагоналями-диаметрами равен 45°.

Найдите на следующих рисунках градусные меры отмеченных углов.

Видео:Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

Geogebra — бесплатное он-лайн геометрическое приложение

Geogebra — наилучшее он-лайн геометрическое приложение для рисования геометрических фигур.
Подождите. Идёт загрузка (прим. 1-2 минуты).
Открыть в полный экран

Открыть в полный экран
Это он-лайн приложение позволяет рисовать геометрические фигуры — точки, линии, углы, треугольники, многоугольники, круги.
Вы можете создавать анимиционную геометрию и слайды.
Если Вам не нужна система координат по умолчанию, Вы можете скрыть ее.