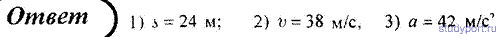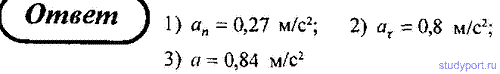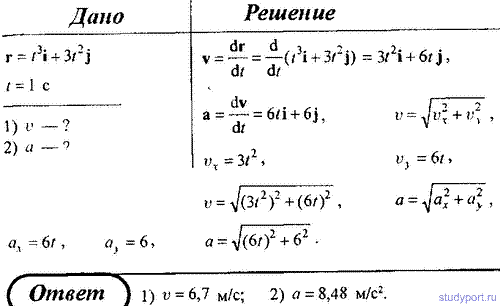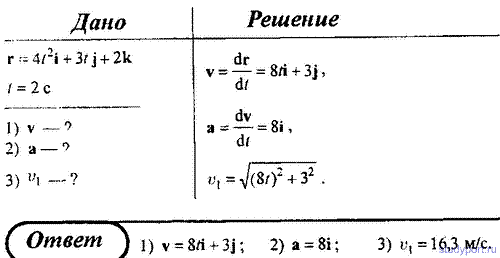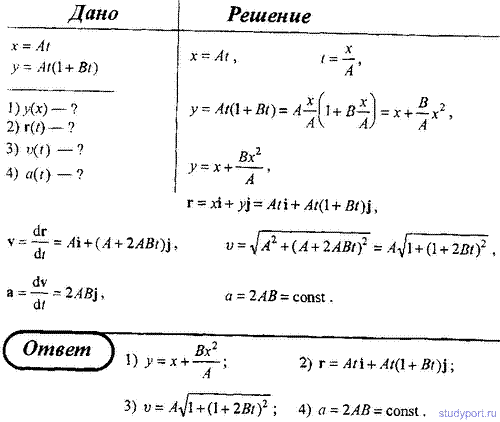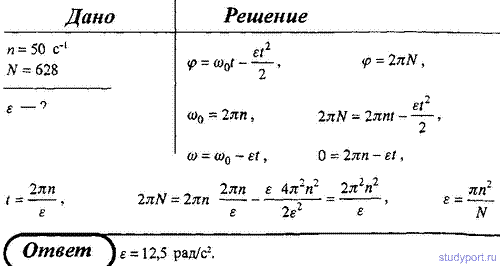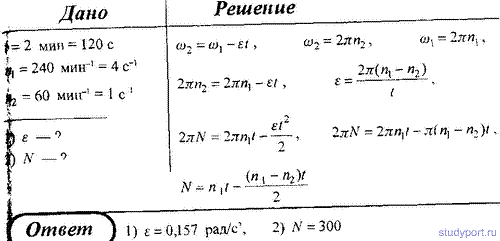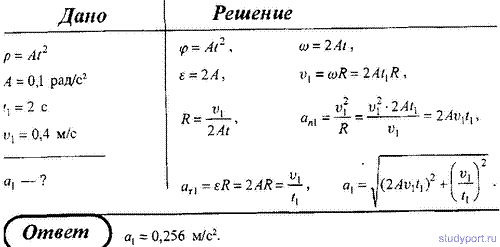Материальная точка движется по окружности радиусом 12 5 (4 видео)

Материальная точка движется по окружности радиусом 12 5

постоянное тангенциальное ускорение

Материальная точка массой m = 20 г движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением. К концу пятого оборота после начала движения кинетическая энергия материальной точки оказалась равной 6,3 мДж. Определить тангенциальное ускорение.

За промежуток времени τ = 10,0 с точка прошла половину окружности радиуса R = 160 см. Вычислить за это время: а) среднюю скорость (v); б) модуль среднего вектора скорости | |; в) модуль среднего вектора полного ускорения | |, если точка двигалась с постоянным тангенциальным ускорением.

За промежуток времени τ = 10,0 с частица прошла половину окружности радиусом R = 160 см с постоянным тангенциальным ускорением. Вычислить за это время а) средний модуль скорости | |; б) модуль среднего вектора полного ускорения | |.

Материальная точка начинает двигаться без начальной скорости по окружности радиусом R = 20 см с постоянным тангенциальным ускорением a_τ = 5 см/с 2 . Через какое число оборотов после начала движения нормальное ускорение точки станет равным тангенциальному?

Точка движется по кривой с постоянным тангенциальным ускорением а_τ = 0,5 м/с 2 . Определить полное ускорение а точки на участке кривой с радиусом кривизны R = 3 м, если точка движется на этом участке со скоростью v = 2 м/с.

Первоначально покоившееся тело прошло за время t = 10 с полторы окружности радиуса R = 5 м с постоянным тангенциальным ускорением. Вычислить соответствующие этому промежутку времени значения: а) среднего модуля скорости , б) модуля средней скорости | |, в) модуля среднего ускорения ||.

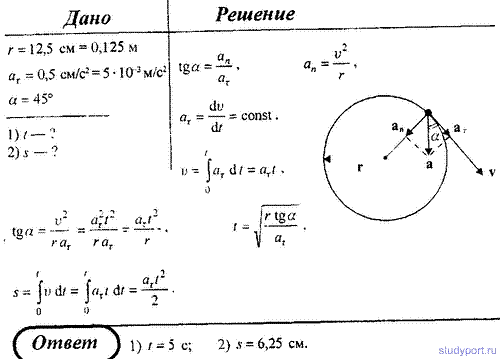
Материальная точка начинает двигаться по окружности радиусом r = 12,5 см с постоянным тангенциальным ускорением а_τ = 0,5 см/с 2 . Определите: 1) момент времени, при котором вектор ускорения а образует с вектором скорости v угол α = 45°; 2) путь, пройденный за это время движущейся точкой.

Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 10 см с постоянным тангенциальным ускорением а_τ = 0,4 см/с 2 . Через промежуток времени t вектор полного ускорения а образует с вектором мгновенной скорости v угол β = 60°. Определить t.

Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 20 см с постоянным тангенциальным ускорением а_τ. Через промежуток времени t = 5,0 с вектор полного ускорения а образует с вектором мгновенной скорости v = 0,02 м/с угол β. Определить a.

Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 30 см с постоянным тангенциальным ускорением а_τ = 0,5 см/с 2 . Через промежуток времени t вектор полного ускорения а образует с вектором мгновенной скорости v угол β = 45°. Определить v.

Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R с постоянным тангенциальным ускорением а_τ. Через промежуток времени t = 6,5 с вектор полного ускорения а = 0,8 см/с 2 образует с вектором мгновенной скорости v = 0,03 м/с угол β. Определить β.

Материальная точка начинает двигаться по часовой стрелке по окружности радиусом R = 50 см с постоянным тангенциальным ускорением а_τ = 0,5 см/с 2 . Через промежуток времени t вектор полного ускорения а = 0,9 см/с 2 образует с вектором мгновенной скорости v угол β. Определить v.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Материальная точка начинает двигаться по окружности радиусом 12,5 м с постоянным тангенциальным ускорением 0,5 м/с2 .

🎓 Заказ №: 21979

⟾ Тип работы: Задача

📕 Предмет: Физика

✅ Статус: Выполнен (Проверен преподавателем)

🔥 Цена: 149 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

Материальная точка начинает двигаться по окружности радиусом 12,5 м с постоянным тангенциальным ускорением 0,5 м/с2 . Определить угол, который образует вектор полного ускорения с вектором скорости через 5 секунд после начала движения. Дано: R  12,5 м 2 0,5 с м a  t  5 с Найти:  ?

Полное ускорение найдем согласно формулы: 2 2 a  an  a (1) Где  a – тангенциальное ускорение; n a – нормальное ускорение точек. Поскольку точка двигается по окружности с постоянным тангенциальным ускорением, то можем записать: a t    Где  – скорость движения точки; t – время;  a – тангенциальное ускорение. Запишем выражение для нормального ускорения: R

Научись сам решать задачи изучив физику на этой странице:

Решение задач по физике

Услуги:

Заказать физику
Помощь по физике

Готовые задачи по физике которые сегодня купили:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Материальная точка движется по окружности радиусом R с постоянной по модулю скоростьюСкачать

Кинематика

21. Тело движется равноускоренно с начальной скоростью v₀. Определить ускорение тела, если за время t оно прошло путь S и его скорость v.

22. Материальная точка движется вдоль прямой так, что её ускорение линейно растёт и за первые 10 секунд достигает значения 5 м/с 2 . Определить в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь.

23. Кинетические уравнения движения двух материальных точек имеют вид x₁ = A₁*t + B₁*t 2 + C₁*t 3 и x₂ = A₂*t + B2*t 2 + C₂*t 3 , где B₁ = 4 м/с 2 , C₁ = – 3 м/с 3 , B2 = -2 м/с 2 C2 = 1 м/c 3 . Определите момент времени, для которого ускорения этих точек будут равны.

24. Кинетические уравнения движения двух материальных точек имеют вид x₁ = A₁ + B₁*t + C₁*t 2 и x₂ = A₂ + B₂*t + C₂*t 2 , где B₁ = B₂, C₁ = – 2 м/с 2 , C₂ = 1 м/c 2 . Определить: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорение a₁ и a₂ для этого момента.

25. Нормальное ускорение точки, движущейся по окружности радиусом r = 4 м, задается уравнением a_n = A + B*t + С*t 2 (A = 1 м/c 2 , B = 6 м/с 3 , С = 9 м/с 4 ) Определите: 1) тангенсальное ускорение точки; 2) путь, пройденный точкой за время t = 5 сек. после начала движения; 3) полное ускорение для момента времени t₂ = 1 секунде.

26. Зависимость пройденного телом пути sот времени tвыражается уравнением s= At— Bt 2 + Ct 3 (A= 2 м/с, В = 3 м/с 2 , С = 4 м/с 3 ). Запишите выражения для скорости и ускорения. Определите для момента времени t— 2 с после начала движения 1) пройденный путь; 2) скорость; 3) ускорение.

27. Зависимость пройденного телом пути по окружности радиусом r= 3 м задается уравнением s= At 2 + Bt(А = 0,4 м/с : , B = 0,1 м/с) Определите для момента времени t = 1 с после начала движения ускорение: 1) нормальное, 2) тангенциальное; 3) полное.

28. Точка движется в плоскости ху из положения с координатами х₁ = v₁ = 0 со скоростью v = ai+ bxj(а, b— постоянные, i, j — орты осей x и y). Определите: 1) уравнение траектории точки y(x); 2) форму траектории.

29. Радиус-вектор материальной точки изменяется со временем по закону r = t 3 i+ 3t 2 j, где i, j — орты осей х и у. Определите для момента времени t = 1 с: 1) модуль скорости; 2) модуль ускорения.

30. Радиус-вектор материальной точки изменяется со временем по закону r = 4t 2 i+ 3tj + 2k. Определите: 1) скорость v; 2) ускорение а; 3) модуль скорости в момент времени t= 2 с.

31. Движение материальной точки в плоскости ху описывается законом х = At, у = At (1 + Bt), где A и B— положительные постоянные. Определите: 1) уравнение траектории материальной точки y(х); 2) радиус-вектор r точки в зависимости от времени; 3) скорость vточки в зависимости от времени; 4) ускорение а точки в зависимости от времени.

32. Материальная точка начинает двигаться по окружности радуисом r = 12,5 с постоянным тангенсальным ускорением а_τ = 0,5 см/с 2 . Определить: 1) момент времени, при котором вектор ускорения a образует с вектором скорости v угол α = 45; 2) путь, пройденный за это время движущейся точкой.

33. Линейная скорость v₁ точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость v₂точки, находящейся на 6 см ближе к его оси. Определите радиус диска.

34. Колесо вращается с постоянным угловым ускорением ε = 3рад/с. Определить радиус колеса, если через время t = 1 с после начала движения полное ускорение колеса равно а = 7,5 м/с 2 .

35. Якорь электродвигателя, имеющий частоту вращения n = 50, после выключения тока, сделав N = 628 оборотов, остановился. Определить угловое ускорение ε якоря.

36. Колесо автомобиля вращается равнозамедленно. За время t = 2 мин оно изменило частоту вращения от 240 до 60 мин -1 . Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.

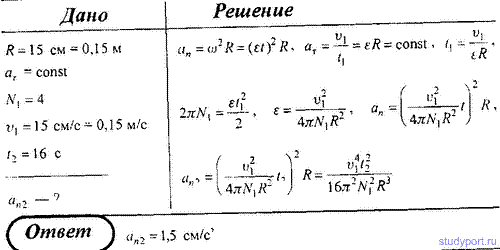
37. Точка движется по окружности радиусом R = 15 см с постоянным тангенсальным ускорением a_τ. К концу четвертого оборота после начала движения линейная скорость точки v₁ = 15 см/с. Определить нормальное ускорение a_n2 точки через t ₂ = 16 c после начала движения.

38. Диск радиусом R = 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота диска от времени задается уравнением φ = A + Bt+ Сt 2 + Dt 3 (B = 1 рад/с, C = 1 рад/с 2 , D = 1 рад/с 3 ). Определите для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение а_τ; 2) нормальное ускорение а_n; 3) полное ускорение а.

39. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt 2 (A = 0,5 рад/с 2 ). Определить к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное a_τ, нормальное a_n и полное ускорение а.

40. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt 2 (A = 0,1 рад/с 2 ). Определить полное ускорение a точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки v = 0,4 м/с.