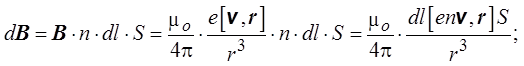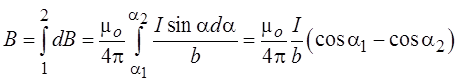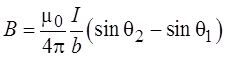Магнитная индукция стороны треугольника (7 видео)

По контуру в виде равностороннего треугольника течёт постоянный ток силой I = 40 А. Длина стороны треугольника а = 0,3 м. Найти магнитную

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
Расчёт магнитных полей с помощью закона Био–Савара–Лапласа. Магнитное поле в веществе (Главы 3-4 учебного пособия по общей физике)
Страницы работы
Содержание работы
3.4. Расчёт магнитных полей с помощью закона
Био–Савара–Лапласа
3.4.1. Индукция магнитного поля отрезка прямолинейного проводника с током
3.4.2. Индукция магнитного поля бесконечно длинного
прямолинейного проводника с током
3.4.3. Индукция магнитного поля в центре квадрата
3.4.4. Расчёт магнитного поля замкнутого кругового тока
(витка с током).
По контуру в виде равностороннего треугольника протекает ток I = 9 А. Длина стороны треугольника a = 3 см. Определить напряжённость и индукцию магнитного поля
Описание и исходные данные задания, 50% решения + фотография:
💡 Видео

Видео:Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Ваш ответ

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

решение вопроса

Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать

Расчёт магнитных полей с помощью закона Био–Савара–Лапласа. Магнитное поле в веществе (Главы 3-4 учебного пособия по общей физике)

Страницы работы

Содержание работы

где v – скорость направленного движения свободных носителей заряда. Умножив В на количество свободных носителей заряда в элементе проводника dl, получим индукцию магнитного поля, созданную этим элементом проводника с током,

;

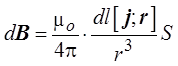
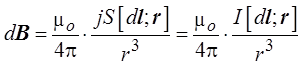
Таким образом, индукция магнитного поля, созданного элементом dl проводника с током I на расстоянии r от элемента проводника, определяется выражением

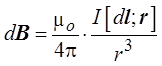
Это выражение и представляет собой закон Био–Савара–Лапласа.

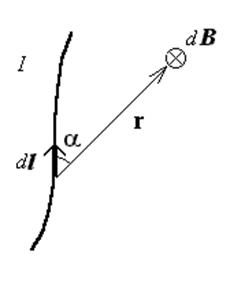
Из закона видно, что вектор магнитной индукции dB всегда перпендикулярен плоскости, в ко-торой лежат векторы dl и r. Его направление определяется по правилу правого винта.

Модуль вектора dB определяется из выражения

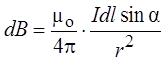
где a – угол между векторами dl и r.

* Здесьj – вектор плотности тока.

Необходимо учесть, что полученное выражение позволяет рассчитать индукцию магнитного поля, созданную одним бесконечно малым элементом проводника dl с током I.

Для того чтобы найти магнитную индукцию, созданную всемпроводником, необходимо использовать принцип суперпозиции, т. е. просуммировать векторы dB, созданные каждым элементом проводника в интересующей нас точке.

Видео:Физика 9 класс (Урок№19 - Индукция магнитного поля.)Скачать

3.4. Расчёт магнитных полей с помощью закона

Видео:ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ сила Ампера правило левой рукиСкачать

Био–Савара–Лапласа

3.4.1. Индукция магнитного поля отрезка прямолинейного проводника с током

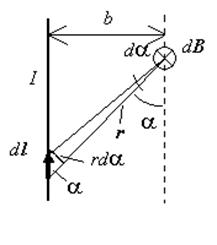
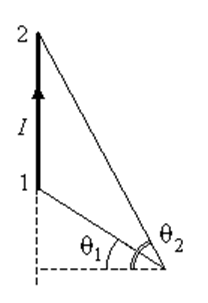
Для всех бесконечно малых элементов dl отрезка векторы dl и r лежат в плоскости листа. Поэтому векторы dB, созданные в выбранной нами точке различными элементами проводника направлены одинаково – перпендикулярно плоскости листа. Следовательно, сложение векторов dB можно заменить сложением их модулей dB.

Из рисунка видно, что r = b/sina
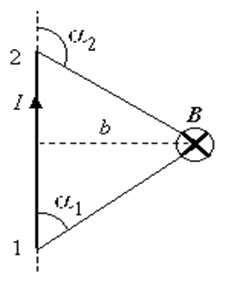
(b – расстояние от проводника до инте-ресующей нас точки), и

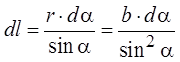
Тогда индукция, созданная элементом проводника dl, равна

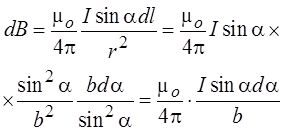
Индукция магнитного поля, созданного всем проводником, может быть найдена как интеграл от dB в пределах от a₁ до + a₂:

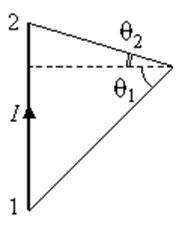
Иногда удобнее воспользоваться другим выражением:

(обратите внимание на рисунок, показывающий углы q₁ и q₂).

Обратите также внимание на то, что если точка расположена так, как показано на следующем рисунке, то q₂ меняет знак и формула для расчёта магнитного поля прямолинейного отрезка записывается следующим образом:

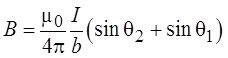
3.4.2. Индукция магнитного поля бесконечно длинного

прямолинейного проводника с током

Если длина прямого проводника бесконечно велика, то a₁ = 0, а a₂ = p.

В этом случае индукция магнитного поля, созданного проводником, будет равна

Таким образом, индукция магнитного поля, созданного бесконечно длинным проводником прямо пропорциональна току в проводнике и обратно пропорциональна расстоянию от проводника до интересующей нас точки.

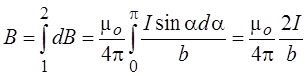
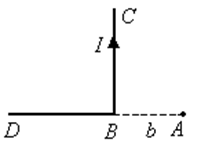
Дополнительно рассмотрим магнитное поле, созданное бесконечным проводником, который изогнут под прямым углом.

Ограничимся получением расчётной формулы для точки А, расположенной на продолжении одной из половин проводника.

Участок DB в точке А не создаёт магнитного поля, так как для него a₁ и a₂ равны 0.

Для участка ВС a₁ = 90 0 , a₂ = -180 0 . Поэтому индукция, созданная этим участком, равна

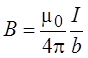
Таким образом, индукция магнитного поля в точке А равна половине индукции, созданной прямым бесконечно длинным проводником с таким же током.

3.4.3. Индукция магнитного поля в центре квадрата

Рассмотрим квадрат со стороной а, в котором течёт ток I.

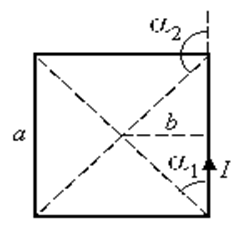
Все стороны квадрата создают в его центре одинаковое магнитное поле. Поэтому если индукция, созданная одной стороной, равна В, то магнитная индукция, созданная всеми сторонами, равна 4В.

В рассматриваемом случае a₁ = 45 0 , а a₂ = 135 0 (см. рисунок).

Индукция магнитного поля, созданного одной стороной, равна:

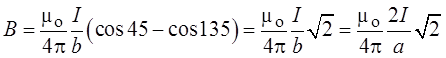
Соответственно индукция магнитного поля, созданного всеми сторонами, равна

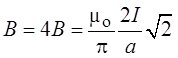
В показанном на рисунке случае индукция магнитного поля направлена перпендикулярно плоскости квадрата на нас.

3.4.4. Расчёт магнитного поля замкнутого кругового тока

(витка с током).

Пусть радиус витка равен R, а ток в нём – I.

Вначале рассмотрим расчёт поля в центре витка.

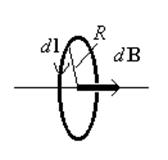
Каждый элемент тока будет создавать индукцию, направленную вдоль оси витка. Поэтому, как и в предыдущем случае, сложение dB алгебраическое и

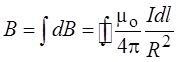
(в каждой точке a = 90 0 )

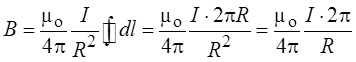
Поле на оси витка на расстоянии b от центра витка рассчитывается несколько сложнее. В этом случае векторы dB не параллельны друг другу.

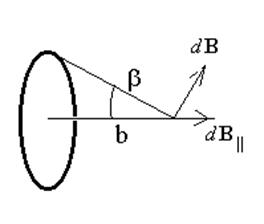
При суммировании составляющие векторов dB, перпендикулярные оси, уничтожаются, а параллельные оси – складываются.

Из рисунка видно, что

;

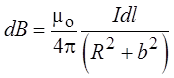
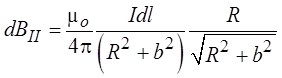
Проинтегрировав это выражение по всему контуру, получаем

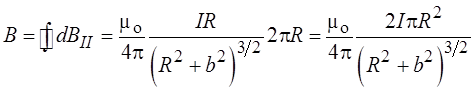
Видео:Электромагнитная индукция. Простыми словамиСкачать

По контуру в виде равностороннего треугольника протекает ток I = 9 А. Длина стороны треугольника a = 3 см. Определить напряжённость и индукцию магнитного поля

Готовое решение: Заказ №8367

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 18.08.2020

Цена: 118 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

По контуру в виде равностороннего треугольника протекает ток I = 9 А. Длина стороны треугольника a = 3 см. Определить напряжённость и индукцию магнитного поля в точке пересечения высот треугольника. (H = 430 А/м, B = 540 мкТл)

Для нахождения магнитной индукции , создаваемой в центре контура одной стороной, воспользуемся формулой для индукции от проводника конечных размеров: , где Гн/м – магнитная постоянная; − расстояние от точки, для которой определяется магнитная индукция, до проводника; − угол между направлением тока в проводнике и вектором, проведённым из точки проводника в точку, для которой определяется магнитная индукция. Для равностороннего треугольника расстояние от точки пересечения высот до стороны равно 1/3 высоты:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.