Любой многоугольник можно вписать в окружность верно или нет (7 видео)

Вписанные и описанные многоугольники

Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности.

Описанной около многоугольника окружностью называется окружность, проходящая через его вершины. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон.

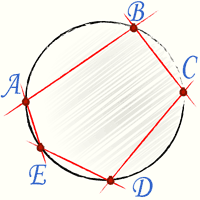Любой многоугольник можно вписать в окружность верно или нет

Вписанный многоугольник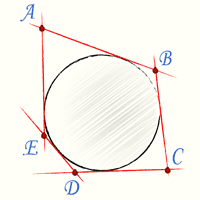

Описанный многоугольник

Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Только многоугольники соответствующие некоторым правилам можно описать окружностью или вписать в них окружность.

Содержание

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них
Многоугольник. Свойства четырехугольников вписанных в окружность.
Любой многоугольник можно вписать в окружность верно или нет
🌟 Видео

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для треугольника всегда возможны и вписанная окружность и описанная окружность.

Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы. Из всех параллелограммов только в ромб и квадрат можно вписать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. Ее центр лежит на пересечении диагоналей.

Вокруг трапеции возможно описать окружность или в трапецию можно вписать окружность если трапеция равнобокая.

Видео:В любой треугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Многоугольник. Свойства четырехугольников вписанных в окружность.

Если все вершины какого-нибудь многоугольника (ABCDE) лежат на окружности, то говорят, что этот многоугольник вписан в окружность, или что окружность описана около него.

Теорема.

В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым углам (2d).

Обратная теорема:

Если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым углам (2d), то около него можно описать окружность.

Пусть ABCD — вписанный выпуклый четырехугольник. Необходимо обосновать, что:

Углы B и D, как вписанные будут равны: первый — половиной дуги ADС, второй — половиной дуги ABС. Следовательно, B + D равняется полусумме дуг ADС и ABС, т.е. половиной окружности. Значит, B + D = 2d. Подобно этому убедимся, что A + С= 2d .

Необходимо обосновать, что около такого четырехугольника можно описать окружность. Через какие-нибудь три его вершины, например, A, B, С прочертим окружность (что всегда можно сделать).

Четвертая вершина D должна располагаться на этой окружности, потому что в противном случае угол D лежал бы своей вершиной или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги ABС, поэтому сумма B + D не измерялась бы полусуммой дуг ADС и ABС, т.е. сумма B + D не равнялась бы 2d, что противоречит условию.

Следствия.

1. Из всех параллелограммов только около прямоугольника можно описать окружность.

2. Около трапеции можно описать окружность только тогда, когда она равнобедренная.

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Любой многоугольник можно вписать в окружность верно или нет

Какое из следующих утверждений верно?

1) Любой прямоугольник можно вписать в окружность.

2) Все углы ромба равны.

3) Треугольник со сторонами 1, 2, 4 существует.

Проверим каждое из утверждений.

1) « Любой прямоугольник можно вписать в окружность.» — верно, выпуклый четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположныхх углов этого четырёхугольника равна 180°.

2) «Все углы ромба равны.» — неверно, противоположные углы ромба равны.

3) «Треугольник со сторонами 1, 2, 4 существует.» — неверно, для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.