Луч отрезок угол треугольника (3 видео) | Курс школьной геометрии

Луч отрезок угол треугольника

Часть прямой, ограниченная двумя точками, называется отрезком.

Через любые две точки можно провести прямую, и притом только одну.

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Точка, которая лежит на прямой, разделяет ее на две части, каждая из которых называется лучом, исходящим из этой точки. Точка — начало луча.

Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало — вершиной угла.

Угол разделяет плоскость на две части — внутреннюю и внешнюю.

Угол называется развернутым, если обе его стороны лежат на одной прямой. В этом случае любая область плоскости является внутренней областью угла.

Содержание

Равенство геометрических фигур
Треугольник. Медиана, биссектриса, высота, средняя линия.
теория по математике 📈 планиметрия
Виды треугольников по углам
Виды треугольников по сторонам
Медиана, биссектриса, высота, средняя линия треугольника
Медиана
Биссектриса
Высота
Средняя линия
Луч отрезок угол треугольника
Опорный конспект «Прямая. Окружность. Угол»
Ответы на вопросы к теме «Прямая. Окружность. Угол»
🌟 Видео

Видео:Математика 1 класс (Урок№10 - Точка. Кривая линия. Прямая линия. Отрезок. Луч. Ломаная линия.)Скачать

Равенство геометрических фигур

Две геометрические фигуры называются равными, если их можно совместить наложением.

Точка отрезка, делящая его пополам, т.е. на два равных отрезка, называется серединой отрезка.

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.

Видео:Отрезок, луч, прямаяСкачать

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Остроугольные	Тупоугольные	Прямоугольные
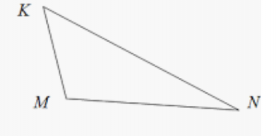
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0 . Такой угол в любом прямоугольном треугольнике – единственный.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Видео:Геометрия 7 класс (Урок№2 - Луч и угол.)Скачать

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Математика 5 класс (Урок№21 - Прямая, луч, отрезок.)Скачать

Луч отрезок угол треугольника

Наглядная геометрия 7 класс. Опорный конспект № 1 «Прямая. Окружность. Угол».

Геометрия изучает геометрические фигуры и их свойства. Простейшие (основные) фигуры: точка, прямая, плоскость. Вы знаете и другие фигуры: луч, отрезок, угол, окружность, треугольник, параллелепипед.

Математическая точка не бывает большой или маленькой. Она не имеет размеров. Математическая точка — это воображаемая точка, хотя мы ее и рисуем.

Что такое прямая? На этот вопрос нельзя ответить. Прямую можно представить как туго натянутую бесконечную нить или как тонкий луч света, пролетающий в бесконечном пространстве. Прямая не имеет толщины, но бесконечна в обе стороны. Прямая на плоскости разбивает плоскость на две полуплоскости.

Если на прямой отметить точку, то получим два луча. Два луча, выходящие из одной точки, образуют угол. Если на прямой взять две точки, то получим отрезок. Отрезки, соединенные последовательно концами, образуют ломаную. Замкнутая ломаная образует многоугольник.

Одно из самых первых свойств: «Через две точки проходит единственная прямая». Его принимают без доказательства. Свойства, которые принимают без доказательства, называются аксиомами. Свойства, истинность которых устанавливается путем логических рассуждений, называются теоремами.

Опорный конспект «Прямая. Окружность. Угол»

Свойства прямой. Через две точки можно провести единственную прямую. Если две прямые пересекаются, то в единственной точке. В двух точках пересекаться они не могут, так как через две точки можно провести единственную прямую.

Прямые называются параллельными, если они ЛЕЖАТ В ОДНОЙ ПЛОСКОСТИ и не пересекаются, сколько бы их ни продолжали. Требование, чтобы прямые лежали в одной плоскости, обязательно. Существуют прямые, которые не пересекаются и в то же время не параллельны. Они называются скрещивающимися (представьте реку и мост через нее). На рисунке это две прямые, проходящие через указанные ребра куба.

Части прямой — это отрезок и луч.

Отрезок — это часть прямой, ограниченная двумя точками. Равными называются отрезки, которые совпадают при наложении. Если на отрезке отметить точку, то она разобьет его на два отрезка, сумма длин которых равна длине данного отрезка.

Луч — это часть прямой, ограниченная одной точкой. Поэтому он бесконечен в одну сторону. Два луча называются противоположными, если они имеют общее начало и дополняют друг друга до прямой.

Фигура, которую можно составить из отрезков, последовательно соединенных концами, — ломаная. Если начало первого отрезка совпадает с концом последнего, то такая ломаная называется замкнутой. Если звенья ломаной не пересекаются и соседние звенья не лежат на одной прямой, то она называется простой. Изображенная на рисунке звездочка — замкнутая ломаная из пяти звеньев, которая не является простой ломаной.

Окружность — это фигура, которая состоит из всех точек плоскости, равноудаленных от данной. Важная часть определения ИЗ ВСЕХ ТОЧЕК ПЛОСКОСТИ. Если опустить «из всех точек», то можно получить дугу окружности. Она тоже состоит из точек плоскости, равноудаленных от данной. А если опустить «плоскости», то можно получить сферу. Она тоже состоит из точек, равноудаленных от данной. С окружностью связано семь элементов: радиус, дуга, хорда, диаметр, круг, сектор, сегмент. Иногда путают круг и окружность. Окружность — ЭТО ЛИНИЯ, а круг — это часть плоскости, ограниченная окружностью.

Два луча, выходящие из одной точки, образуют угол. Равными называются углы, которые совпадают при наложении. Биссектрисой угла называется луч, который выходит из вершины и делит его на два равных угла.

Различают развернутый, прямой, острый, тупой и полный углы. Развернутым называется угол, образованный противоположными лучами. Развернутый угол равен 180°, прямой — 90°, острый — меньше 90°, тупой — больше 90°, но меньше 180°. Если увеличивать развернутый угол, то получим сверхтупой угол, а когда стороны угла совпадут — полный угол. Полный угол равен 360° (веер, раскрытый до предела). Ясно, что прямой угол получится, если провести биссектрису развернутого угла.

Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.

Если у двух углов одна сторона общая, а две другие — противоположные лучи, то это СМЕЖНЫЕ углы. Сумма смежных углов равна 180° (они образуют развернутый угол).

При пересечении двух прямых образуется две пары противоположных углов — это ВЕРТИКАЛЬНЫЕ углы (их стороны — противоположные лучи). Вертикальные углы равны (углы 1 и 3 в сумме дают 180° как смежные, и углы 2 и 3 в сумме дают 180° как смежные, отсюда ∠1 = ∠2).

Перпендикулярными называются прямые, которые пересекаются под прямым углом. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, один конец которого является точкой их пересечения. Он называется основанием перпендикуляра. Через точку, лежащую на прямой, можно провести единственную прямую, перпендикулярную данной. То же касается точки, не лежащей на прямой. Очень важной является теорема о двух перпендикулярах: две прямые, перпендикулярные третьей, параллельны между собой (если бы они пересекались, то из точки на прямую можно было бы опустить два перпендикуляра, что невозможно).

Ответы на вопросы к теме «Прямая. Окружность. Угол»

Через две точки проходит единственная прямая. Если две прямые пересекаются, то в единственной точке. В двух точках пересекаться они не могут, так как через две точки проходит единственная прямая.
Параллельными называются прямые, которые лежат в одной плоскости и не пересекаются.
Отрезок — это часть прямой, ограниченная двумя точками.
Равными называются отрезки, которые совпадают при наложении.
Если на отрезке отметить точку, то она разобьет его на два отрезка, сумма длин которых равна длине данного отрезка.
Луч — это часть прямой, ограниченная одной точкой. Противоположными лучами называются два луча, которые имеют общее начало и дополняют друг друга до прямой.
Ломаной называется фигура, состоящая из отрезков, последовательно соединенных концами. Ломаная называется простой, если она не имеет самопересечений и никакие два соседних звена не лежат на одной прямой. Ломаная называется замкнутой, если у нее начало первого отрезка совпадает с концом последнего.
Окружность — множество всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром. Круг — это часть плоскости, ограниченная окружностью. Радиусом называется отрезок, соединяющий центр окружности с любой ее точкой, или длина этого отрезка. Дуга — это часть окружности, ограниченная двумя точками. Хорда — это отрезок, соединяющий две точки окружности. Диаметр — это хорда, проходящая через центр. Сектор — это часть круга, ограниченная двумя радиусами. Сегмент — это часть круга, ограниченная хордой.
Угол — это фигура, образованная двумя лучами, выходящими из одной точки.
Равными называются углы, которые совпадают при наложении.
Биссектрисой угла называется луч, который выходит из вершины и делит его на два равных угла.
Развернутым называется угол, стороны которого являются противоположными лучами.
Один градус — это часть развернутого угла. Развернутый угол равен 180°.
Прямым называется угол, равный 90°. Острым называется угол, меньший 90°. Тупым называется угол, больший 90°, но меньший 180°. Полным называется угол, стороны которого совпадают и который равен 360°.
Если внутри угла из его вершины провести луч, то он разобьет угол на два угла, сумма градусных мер которых равна градусной мере данного угла.
Аксиома — верное утверждение, которое принимается без доказательства.
Теорема — верное утверждение, требующее доказательства путем логического рассуждения.
Смежными называются два угла, у которых одна сторона общая, а две другие — противоположные лучи.
Сумма смежных углов равна 180° (см. на рисунке теорему 1). Доказательство. Общая сторона разбивает развернутый угол на два угла, сумма градусных мер которых равна градусной мере развернутого угла. А развернутый угол равен 180°.
Вертикальными называются два угла, стороны которых являются противоположными лучами (дополнительными полупрямыми).
Вертикальные углы равны (см. на рисунке теорему 2). Доказательство. Углы 1 и 3 — смежные, поэтому в сумме дают 180°. Углы 2 и 3 — смежные, поэтому в сумме дают 180°. Значит, углы 1 и 2 равны.
Перпендикулярными называются прямые, которые пересекаются под прямым углом. Перпендикуляром к данной прямой называется отрезок перпендикулярной прямой, один конец которого является точкой их пересечения. Он называется основанием перпендикуляра.
Из точки на прямой можно восстановить (восставить) единственный перпендикуляр к данной прямой (см. на рисунке теорему 3). Доказательство. Отложим прямой угол от правого луча прямой. Получим перпендикуляр. Отложим прямой угол от левого луча. Если стороны прямых углов не совпадут, то получится три угла, которые образуют развернутый угол и при этом в сумме больше 180°.
Из точки вне прямой можно опустить единственный перпендикуляр на данную прямую (см. на рисунке теорему 4). Доказательство. 1. Совместим верхнюю полуплоскость с нижней (перегнем плоскость по прямой). Данная точка совместится с точкой в нижней полуплоскости. Соединим эти точки. Получим перпендикуляр (так как углы 1 и 2 совпали, то они равны и являются смежными, значит, каждый равен 90°). 2. Если из точки можно опустить еще один перпендикуляр, то, перегнув плоскость еще раз, получим еще два равных прямых угла, а значит, еще одну прямую, проходящую через две точки, что невозможно.
Две прямые, перпендикулярные третьей, параллельны между собой (см. на рисунке теорему 5). Доказательство. Если бы они пересекались, то из точки можно было бы опустить два перпендикуляра на данную прямую. А это невозможно.