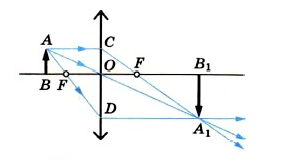
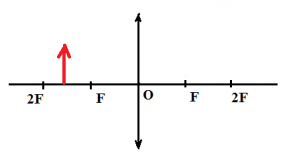
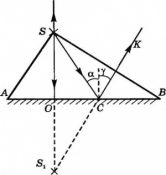
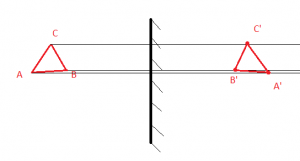
Прямоугольный треугольник с катетами с = 2 см и h = 3 см расположен перед собирающей линзой с фокусным расстоянием F = 10 см, как показано на рисунке.
Чему равна площадь даваемого линзой изображения этого треугольника? Сделайте рисунок с указанием хода лучей.
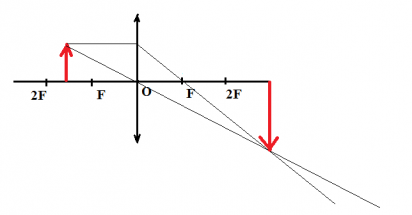
1) Изображение треугольника построено на рисунке.
Изображение точки B удобно найти как пересечение луча, проходящего через центр линзы и луча, падающего на линзу параллельно главной оптической оси.
Изображение точки С находится в точности под изображением точки В. Кроме того, так как катет BC находится в двойном фокусе, то его изображение B’C’ является перевернутым, действительным и длина изображения в точности совпадает с длиной катета: 
2) Используя формулу тонкой линзы, найдем расстояние от линзы до изображения точки А (
)
Горизонтальный катет изображения равен
3) Таким образом, площадь треугольника изображения равна:
Ответ: 
| Критерии оценивания выполнения задания | Баллы | ||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины | 3 | ||||||||||||||||||||||||||||||||||||||||
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.). В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/ вычислениях пропущены логически важные шаги. Отсутствует пункт IV, или в нём допущена ошибка. | 2 | ||||||||||||||||||||||||||||||||||||||||
| Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. Содержание
Видео:8 класс, 29 урок, Линзы. Построение изображений в линзахСкачать  Тонкие линзы. Построение изображений.Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев Темы кодификатора ЕГЭ: построение изображений в линзах, формула тонкой линзы. Правила хода лучей в тонких линзах, сформулированные в предыдущей теме, приводят нас к важнейшему утверждению. Теорема об изображении. Если перед линзой находится светящаяся точка , то после преломления в линзе все лучи (или их продолжения) пересекаются в одной точке .
Точка называется изображением точки . Если в точке пересекаются сами преломлённые лучи, то изображение называется действительным. Оно может быть получено на экране, так как в точке концентрируется энергия световых лучей. Если же в точке пересекаются не сами преломлённые лучи, а их продолжения (так бывает, когда преломлённые лучи расходятся после линзы), то изображение называется мнимым. Его нельзя получить на экране, поскольку в точке не сосредоточено никакой энергии. Мнимое изображение, напомним, возникает благодаря особенности нашего мозга — достраивать расходящиеся лучи до их мнимого пересечения и видеть в этом пересечении светящуюся точку.Мнимое изображение существует лишь в нашем сознании. Теорема об изображении служит основой построения изображений в тонких линзах. Мы докажем эту теорему как для собирающей, так и для рассеивающей линзы. Видео:Урок 396. Построение изображений с помощью линзСкачать  Собирающая линза: действительное изображение точки.Сперва рассмотрим собирающую линзу. Пусть — расстояние от точки до линзы, — фокусное расстояние линзы. Имеются два принципиально разных случая: f’ alt=’a>f’ /> и (а также промежуточный случай ). Мы разберём эти случаи поочерёдно; в каждом из них мы Первый случай: f’ alt=’a>f’ /> . Точечный источник света расположен дальше от линзы, чем левая фокальная плоскость (рис. 1 ).
Луч , идущий через оптический центр, не преломляется. Мы возьмём произвольный луч , построим точку , в которой преломлённый луч пересекается с лучом , а затем покажем, что положение точки не зависит от выбора луча (иными словами, точка является одной и той же для всевозможных лучей ). Тем самым окажется, что все лучи, исходящие из точки , после преломления в линзе пересекаются в точке и теорема об изображении будет доказана для рассматриваемого случая f’ alt=’a>f’ /> . Точку мы найдём, построив дальнейший ход луча . Делать это мы умеем: параллельно лучу проводим побочную оптическую ось до пересечения с фокальной плоскостью в побочном фокусе , после чего проводим преломлённый луч до пересечения с лучом в точке . Теперь будем искать расстояние от точки до линзы. Мы покажем, что это расстояние выражается только через и , т. е. определяется лишь положением источника и свойствами линзы, и не зависит тем самым от конкретного луча . Опустим перпендикуляры и на главную оптическую ось. Проведём также параллельно главной оптической оси, т. е. перпендикулярно линзе. Получим три пары подобных треугольников: В результате имеем следующую цепочку равенств (номер формулы над знаком равенства указывает, из какой пары подобных треугольников данное равенство получено). Но , так что соотношение (4) переписывается в виде: Отсюда находим искомое расстояние от точки до линзы: Как видим, оно и в самом деле не зависит от выбора луча . Следовательно, любой луч после преломления в линзе пройдёт через построенную нами точку , и эта точка будет действительным изображением источника Теорема об изображении в данном случае доказана. Практическая важность теоремы об изображении состоит вот в чём. Коль скоро все лучи источника пересекаются после линзы в одной точке — его изображении — то для построения изображения достаточно взять два наиболее удобных луча. Какие именно? Если источник не лежит на главной оптической оси, то в качестве удобных лучей годятся следующие: — луч, идущий через оптический центр линзы — он не преломляется; Построение изображения с помощью этих лучей показано на рис. 2 .
Если же точка лежит на главной оптической оси, то удобный луч остаётся лишь один — идущий вдоль главной оптической оси. В качестве второго луча приходится брать «неудобный» (рис. 3 ).
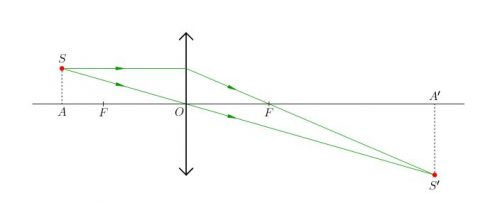
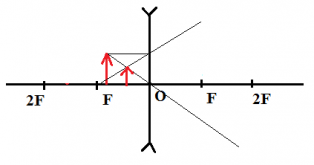
Посмотрим ещё раз на выражение ( 5 ). Его можно записать в несколько ином виде, более симпатичном и запоминающемся. Перенесём сначала единицу влево: Теперь разделим обе части этого равенства на a: Соотношение (7) называется формулой тонкой линзы (или просто формулой линзы). Пока что формула линзы получена для случая собирающей линзы и для f’ alt=’a>f’ /> . В дальнейшем мы выведем модификации этой формулы для остальных случаев. Теперь вернёмся к соотношению (6) . Его важность не исчерпывается тем, что оно доказывает теорему об изображении. Мы видим также, что не зависит от расстояния (рис. 1, 2 ) между источником и главной оптической осью! Это означает, что какую бы точку отрезка мы ни взяли, её изображение будет находиться на одном и том же расстоянии от линзы. Оно будет лежать на отрезке — а именно, на пересечении отрезка с лучом , который пойдёт сквозь линзу без преломления. В частности, изображением точки будет точка . Тем самым мы установили важный факт: изображением отрезка лужит отрезок . Отныне исходный отрезок, изображение которого нас интересует, мы называем предметом и обозначаем на рисунках красной стрелочкой. Направление стрелки нам понадобится для того, чтобы следить — прямым или перевёрнутым получается изображение. Видео:Оптика: построение лучей, площадь треугольникаСкачать  Собирающая линза: действительное изображение предмета.Перейдём к рассмотрению изображений предметов. Напомним, что пока мы находимся в рамках случая f’ alt=’a>f’ /> . Здесь можно выделить три характерных ситуации. 1. . Изображение предмета является действительным, перевёрнутым, увеличенным (рис. 4 ; двойной фокус обозначен ). Из формулы линзы следует, что в этом случае будет 2f’ alt=’b>2f’ /> (почему?).
Такая ситуация реализуется, например, в диапроекторах и киноаппаратах — эти оптические приборы дают на экране увеличенное изображение того, что находится на плёнке. Если вам доводилось показывать слайды, то вы знаете, что слайд нужно вставлять в проектор перевёрнутым — чтобы изображение на экране выглядело правильно, а не получилось вверх ногами. Отношение размера изображения к размеру предмета называется линейным увеличением линзы и обозначается Г — (это заглавная греческая «гамма»): Из подобия треугольников и получим: Формула (8) применяется во многих задачах, где фигурирует линейное увеличение линзы. 2. . В этом случае из формулы (6) находим, что и . Линейное увеличение линзы согласно (8) равно единице, т. е. размер изображения равен размеру предмета (рис. 5 ).
3. 2f’ alt=’a>2f’ /> . В этом случае из формулы линзы следует, что (почему?). Линейное увеличение линзы будет меньше единицы — изображение действительное, перевёрнутое, уменьшенное (рис. 6 ).
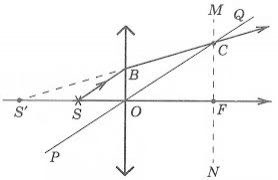
Данная ситуация является обычной для многих оптических приборов: фотоаппаратов, биноклей, телескопов — словом, тех, в которых получают изображения удалённых объектов. По мере удаления предмета от линзы его изображение уменьшается в размерах и приближается к фокальной плоскости. Рассмотрение первого случая f’ alt=’a>f’ /> нами полностью закончено. Переходим ко второму случаю. Он уже не будет столь объёмным. Видео:Как построить ИЗОБРАЖЕНИЕ на ЛИНЗЕ❗Скачать  Собирающая линза: мнимое изображение точки.Второй случай: . Точечный источник света расположен между линзой и фокальной плоскостью (рис. 7 ).
|
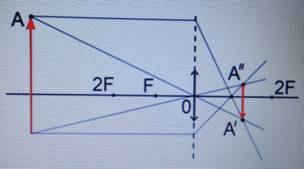
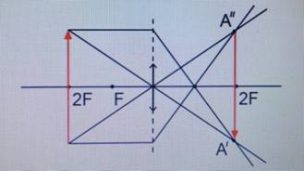
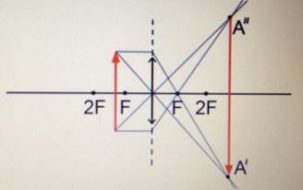
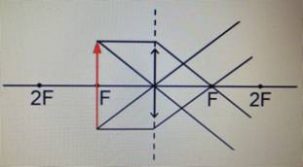
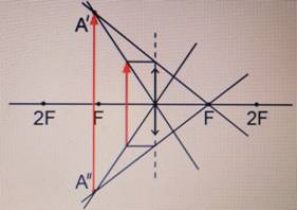
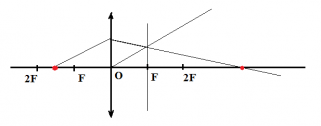
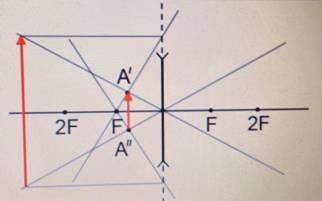
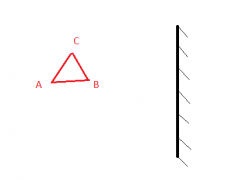
Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
