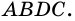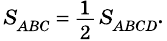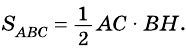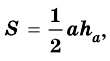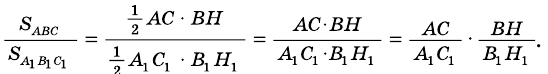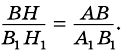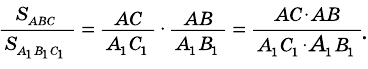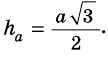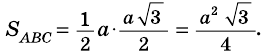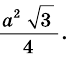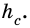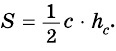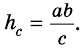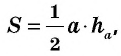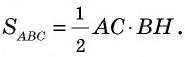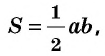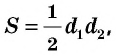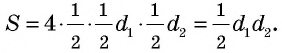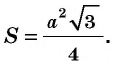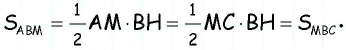Лемма о площадях треугольников (8 видео)

51. Планиметрия Читать 0 мин.

Содержание

51.506. Отношения
Основные свойства площадей треугольников
Площадь треугольника — определение и вычисление с примерами решения
Теорема (формула площади треугольника)
🔍 Видео

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

51.506. Отношения

Зачастую в геометрических задачах в условии даются отношения отрезков и площадей или отношение отрезков нужно найти. Существует ряд теорем и свойств фигур и их элементов, в которых так или иначе используются отношения.

ОТНОШЕНИЯ ОТРЕЗКОВ:

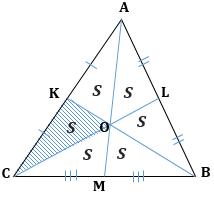
1. Все медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины: AO : AM = 2 : 1.

2. Средняя линия треугольника равна половине основания: $MN = fracBC$

3. Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна ее половине $CM = fracAB$

4. Диагонали параллелограмма точкой пересечения делятся пополам.

Произвольный параллелограмм или ромб:

Прямоугольник или квадрат:

ОТНОШЕНИЯ ПЛОЩАДЕЙ:

1. Медиана разбивает треугольник на два равновеликих (по площади) треугольника: $S_ = S_ = S$

2. Треугольник делится тремя медианами на шесть равновеликих треугольников:

3. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна $fracS$

ЛЕММЫ О ПЛОЩАДЯХ ТРЕУГОЛЬНИКА:

Площади подобных фигур относятся как квадрат коэффициента подобия.

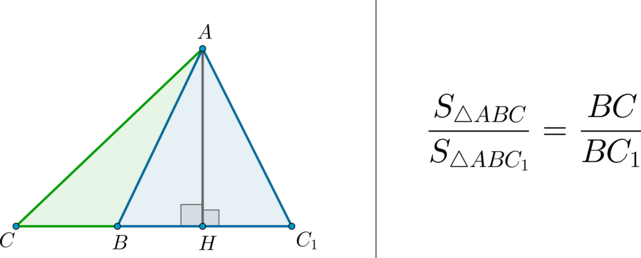
Если стороны треугольников с общей вершиной лежат на одной прямой, то их площади относятся как основания.

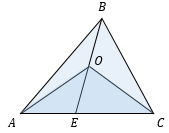
Если два треугольника имеют общую сторону, то их площади соотносятся как длины отрезков BE и OE.

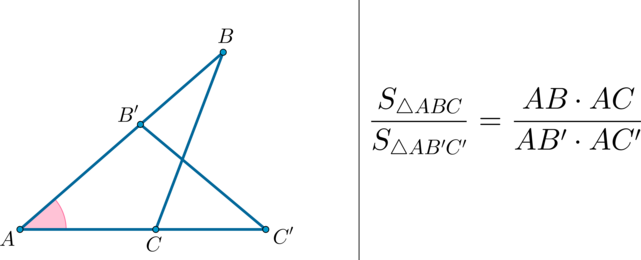
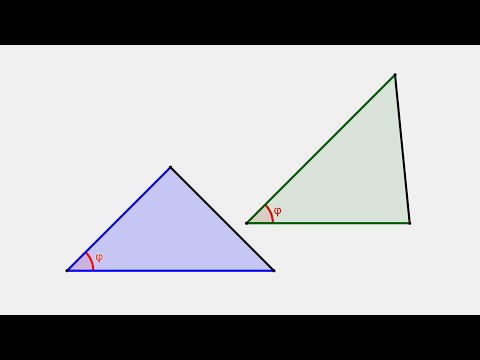
Если два треугольника имеют общий угол, то их площади соотносятся как произведения соответствующих сторон, прилежащих к этому углу.

Лемма 4 применима даже в том случае, если точки нового треугольника были взяты не на сторонах, а на продолжениях сторон. Пусть точка Е лежит на продолжении стороны AB за вершину В.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Основные свойства площадей треугольников

Факт 1.
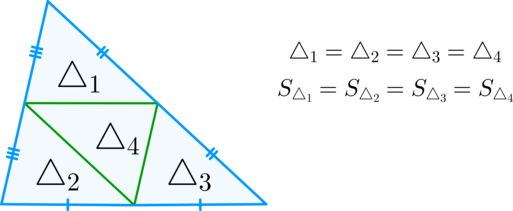
(bullet) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.

Факт 2.
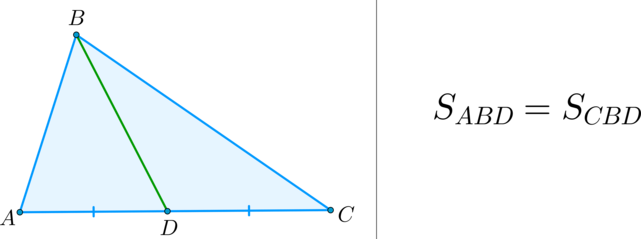
(bullet) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).

Факт 3.
(bullet) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.

Факт 4.
(bullet) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.

Факт 5.
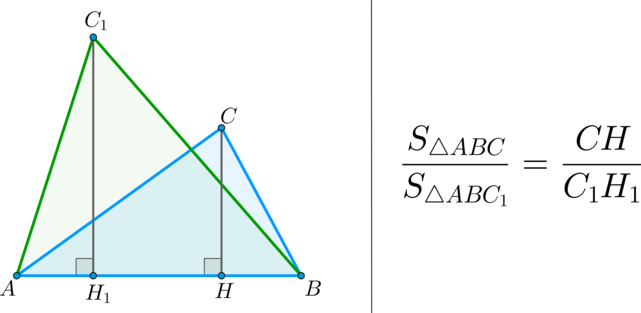
(bullet) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.

Факт 6.
(bullet) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.

Факт 7.
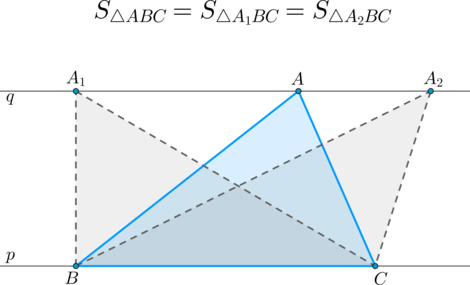
(bullet) Если прямые (p) и (q) параллельны, то

Факт 8.
(bullet) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
(bullet) Отношение периметров подобных треугольников равно коэффициенту подобия.

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Площадь треугольника — определение и вычисление с примерами решения

Площадь треугольника:

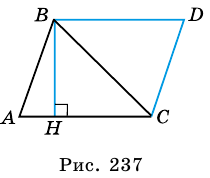
Теорема (о площади треугольника). Площадь треугольника равна половине произведения его стороны на высоту, к ней проведенную.

Доказательство:

Пусть

1) Проведем через вершину прямую, параллельную а через вершину — прямую, параллельную Получим параллелограмм

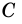
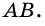
2) (по трем сторонам). Поэтому

откуда

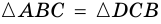
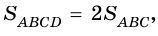
3) Так как 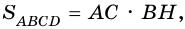то

В общем виде формулу площади 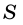треугольника можно записать так:

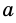
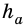
где — сторона треугольника, — высота, проведенная к ней.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.

Следствие 2. Если сторона одного треугольника равна стороне другого треугольника, то площади таких треугольников относятся как их высоты, проведенные к этим сторонам.

Следствие 3. Если высота одного треугольника равна высоте другого треугольника, то площади этих треугольников относятся как стороны, к которым проведены эти высоты.

Пример:

Докажите, что если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих этот угол.

Доказательство:

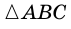
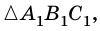
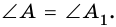
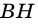
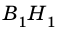
Рассмотрим и у которых Проведем высоты и (рис. 238).

2) (по острому углу), поэтому

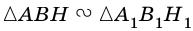
3) Имеем:

Пример:

Найдите площадь равностороннего треугольника, сторона которого равна

Решение:

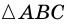
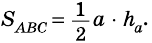
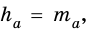
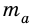
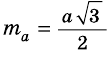
Пусть — равносторонний со стороной Тогда В равностороннем треугольнике где — медиана. Но (§ 18, задача 4), поэтому

Следовательно,

Ответ.

Пример:

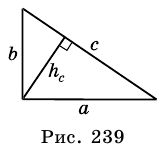
Стороны треугольника равны 8 см, 15 см и ^ 17 см. Найдите высоту треугольника, проведенную к его наибольшей стороне.

Решение:

Так как 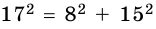(т. е. 289 = 289), то по теореме, обратной теореме Пифагора, треугольник является прямоугольным. Прямой угол является противолежащим к стороне, равной 17 см.

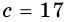
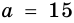
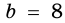
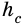
Пусть на рис. 239 изображен прямоугольный треугольник, у которого см -гипотенуза, и см — катеты, — высота. Найдем

Площадь этого треугольника можно найти

по формулам: 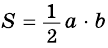или

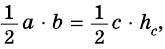
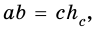
Тогда то есть откуда

Таким образом, имеем: 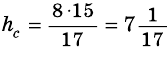(см).

Ответ. 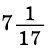см.

Видео:8 класс "Спрятанная" теорема про площади треугольниковСкачать

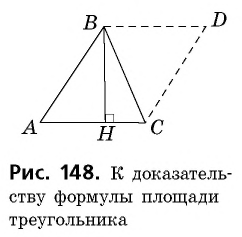
Теорема (формула площади треугольника)

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

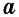
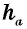
где — сторона треугольника, — проведенная к ней высота.

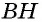
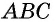
Пусть — высота треугольника (рис. 148). Докажем, что

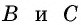
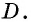
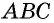
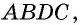
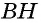
Проведем через вершины прямые, параллельные сторонам треугольника, и обозначим точку их пересечения Таким образом, мы «достроили» треугольник до параллелограмма в котором отрезок также является высотой, проведенной к стороне

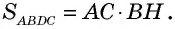
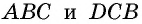
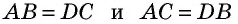
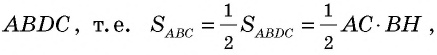
По формуле площади параллелограмма Треугольники равны по трем сторонам (у них сторона общая, как противолежащие стороны параллелограмма). Эти треугольники имеют равные площади. Тогда площадь треугольника составляет половину площади параллелограмма что и требовалось доказать.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов:

где 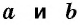— катеты прямоугольного треугольника.

Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.

Следствие 2

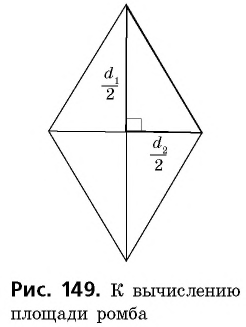
Площадь ромба равна половине произведения его диагоналей:

где 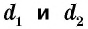— диагонали ромба.

Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами 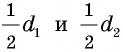(рис. 149). Используя следствие 1, имеем:

Следствие 3

Площадь равностороннего треугольника со стороной 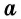вычисляется по формуле

Обоснуйте это следствие самостоятельно.

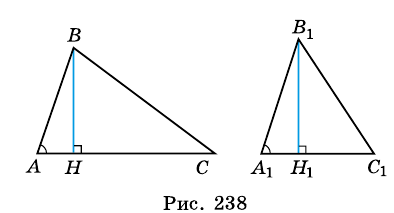
Опорная задача

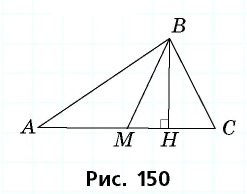
Медиана делит треугольник на два равновеликих треугольника. Докажите.

Решение:

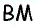
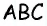
Пусть — медиана треугольника (рис. 150).

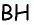
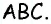
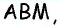
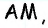
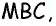
Проведем высоту треугольника Этот отрезок является одновременно высотой треугольника проведенной к стороне и высотой треугольника проведенной к стороне Учитывая равенство отрезков имеем:

Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.

Докажите эти утверждения самостоятельно.

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Соотношения между сторонами и углами произвольного треугольника
Окружность и круг
Описанные и вписанные окружности
Плоские и пространственные фигуры
Взаимное расположения прямых на плоскости
Треугольник
Решение треугольников
Треугольники и окружность

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.